A circular lamina of radius a and centre O has a mass per unit area of kx2, where x is the distance from O and k is a constant. If the mass of the lamina is M, find in terms of M and a, the moment of inertia of the lamina about an axis through O and perpendicular to the lamina.

M=∫a0(dM)
=∫10(2πx)dX(kx2)=πka42
∴πk=2Ma4
now I=∫a0dI=∫aa0(dM)X2
=∫a0(2πkx3)x2=(πk)d63
Substituting the value of πk, we get
I=23Ma2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2 Single Correct
Explore 26 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2 Multiple Correct
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 1 Objective
Explore 30 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe mass of a uniform circular ring of radius 0.2m is 0.1kg. Calcuate the moment of inertia of the ring about an axis passing through its centre an perpendicular to its surface.
View Solution
Knowledge Check
In the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
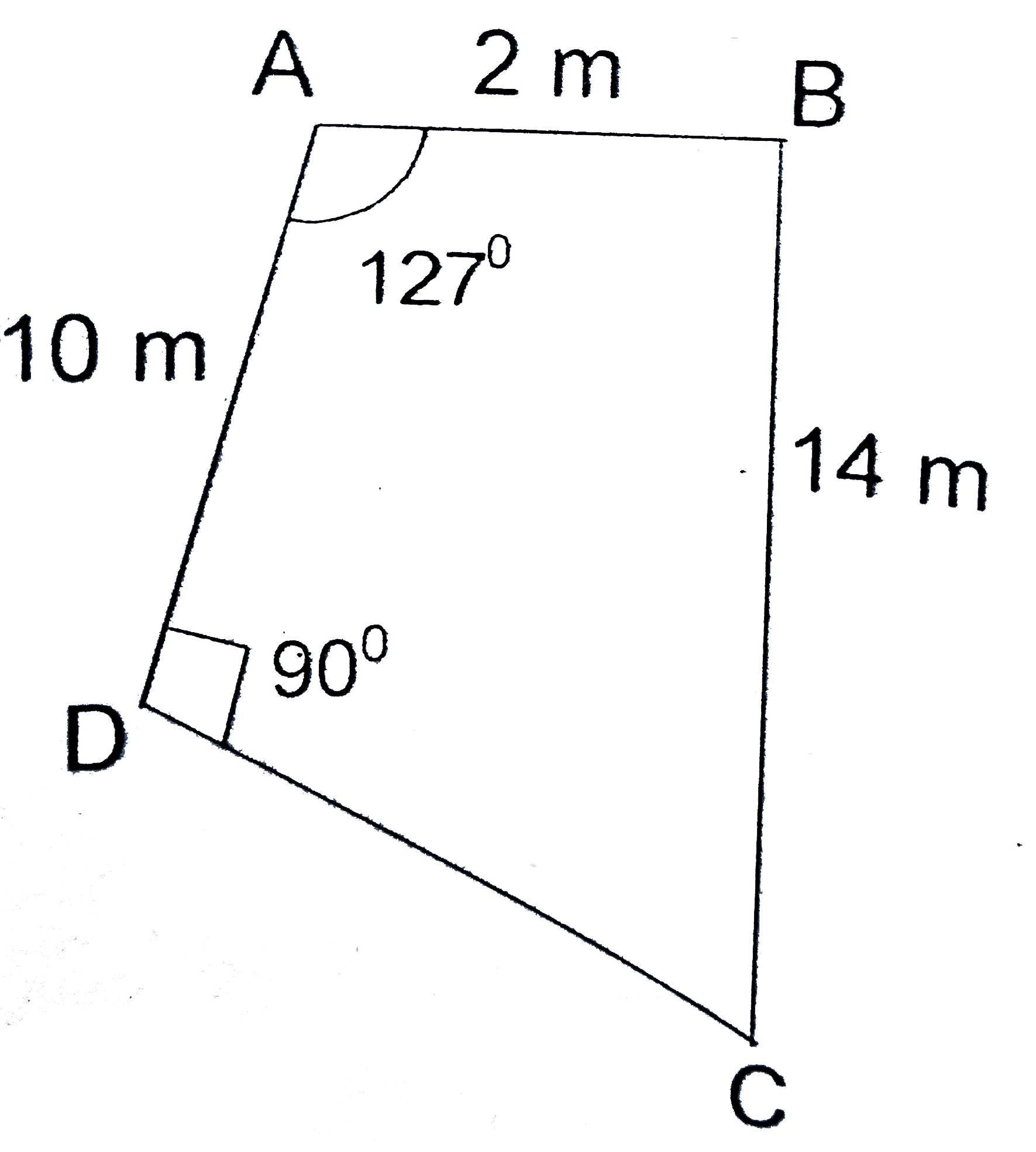 A256kgm2B512kgm2C200kgm2D100kgm2
A256kgm2B512kgm2C200kgm2D100kgm2A hole of radius R/2 is cut from a thin circular plate of raduis R as shown in the figure. If the mass of the remaining plate is M, then find moment of inertia of the plate about an axis through O perpendicular to plane
 A1325MR2B1324MR2C1124MR2D1125MR2
A1325MR2B1324MR2C1124MR2D1125MR2A thin rod of length l and mass m is turned at mid-point O at angle of 60°. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
 Aml2/3Bml26Cml28Dml212
Aml2/3Bml26Cml28Dml212
The moment of inertia of a triangular lamina of mass M about edge AB is equal to?
View SolutionFour thin rods of same mass M and same length l, form a square as shown in figure. Moment of inertia of this system about an axis through centre O and perpendicular to its plane is

View SolutionA hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be

View Solution

