There is one rod of length L. the resistivity of its material is given by ρ=αx+β. Here x is the distance of α point on rod from one of its ends. Assume A as the area of cross section of rod. Find the electrical resistance of the rod.
To find the electrical resistance of a rod with a non-constant resistivity, we can follow these steps:
1. Understanding the Problem:
The resistivity of the rod is given as ρ=αx+β, where x is the distance from one end of the rod. The rod has a length L and a cross-sectional area A.
2. Setting Up the Resistance Formula:
The resistance R of a small segment dx of the rod can be expressed using the formula:
dR=ρdxA
Substituting the expression for ρ:
dR=(αx+β)dxA
3. Integrating to Find Total Resistance:
To find the total resistance R of the rod, we need to integrate dR from x=0 to x=L:
R=∫L0dR=∫L0(αx+β)dxA
This can be simplified to:
R=1A∫L0(αx+β)dx
4. Calculating the Integral:
We can split the integral:
R=1A(∫L0αxdx+∫L0βdx)
- The first integral ∫L0αxdx evaluates to:
α(x22)L0=αL22
- The second integral ∫L0βdx evaluates to:
β(x)L0=βL
5. Combining the Results:
Now, substituting back into the expression for R:
R=1A(αL22+βL)
6. Final Expression for Resistance:
Thus, the total resistance of the rod is:
R=αL22A+βLA
The resistivity of the rod is given as ρ=αx+β, where x is the distance from one end of the rod. The rod has a length L and a cross-sectional area A.
The resistance R of a small segment dx of the rod can be expressed using the formula:
dR=ρdxA
Substituting the expression for ρ:
dR=(αx+β)dxA
To find the total resistance R of the rod, we need to integrate dR from x=0 to x=L:
R=∫L0dR=∫L0(αx+β)dxA
This can be simplified to:
R=1A∫L0(αx+β)dx
We can split the integral:
R=1A(∫L0αxdx+∫L0βdx)
- The first integral ∫L0αxdx evaluates to:
α(x22)L0=αL22
- The second integral ∫L0βdx evaluates to:
β(x)L0=βL
Now, substituting back into the expression for R:
R=1A(αL22+βL)
Thus, the total resistance of the rod is:
R=αL22A+βLA
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:PRACTICE PROBLEMS
Explore 71 Videos
- CURRENT ELECTRICITYBook:MODERN PUBLICATIONChapter:CURRENT ELECTRICITYExercise:CONCEPTUAL QUESTIONS
Explore 35 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Knowledge Check
A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
A23π2f2ml2B43f2ml2C4π2f2ml2DzeroA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
A23π2f2ml2B43f2ml2C4π2f2ml2DZero
The specific resistance of a material of wire changes as ρ=ρ0x along the length of the conductor whose area of cross section is constant and equal to A. Here x is the distance of point on conductor from one end of the wire. Calculate its electric resistance. (Given the length of the wire is L)
View SolutionA rod PQ of length L revolves in a horizontal plane about the axis YY´. The angular velocity of the rod is w. If A is the area of cross-section of the rod and r be its density, its rotational kinetic energy is
View SolutionA uniform rod of length l is given an impulse at right angles to its length as shown. Find the distance of instantaneous centre of rotation from the centre of the rod.
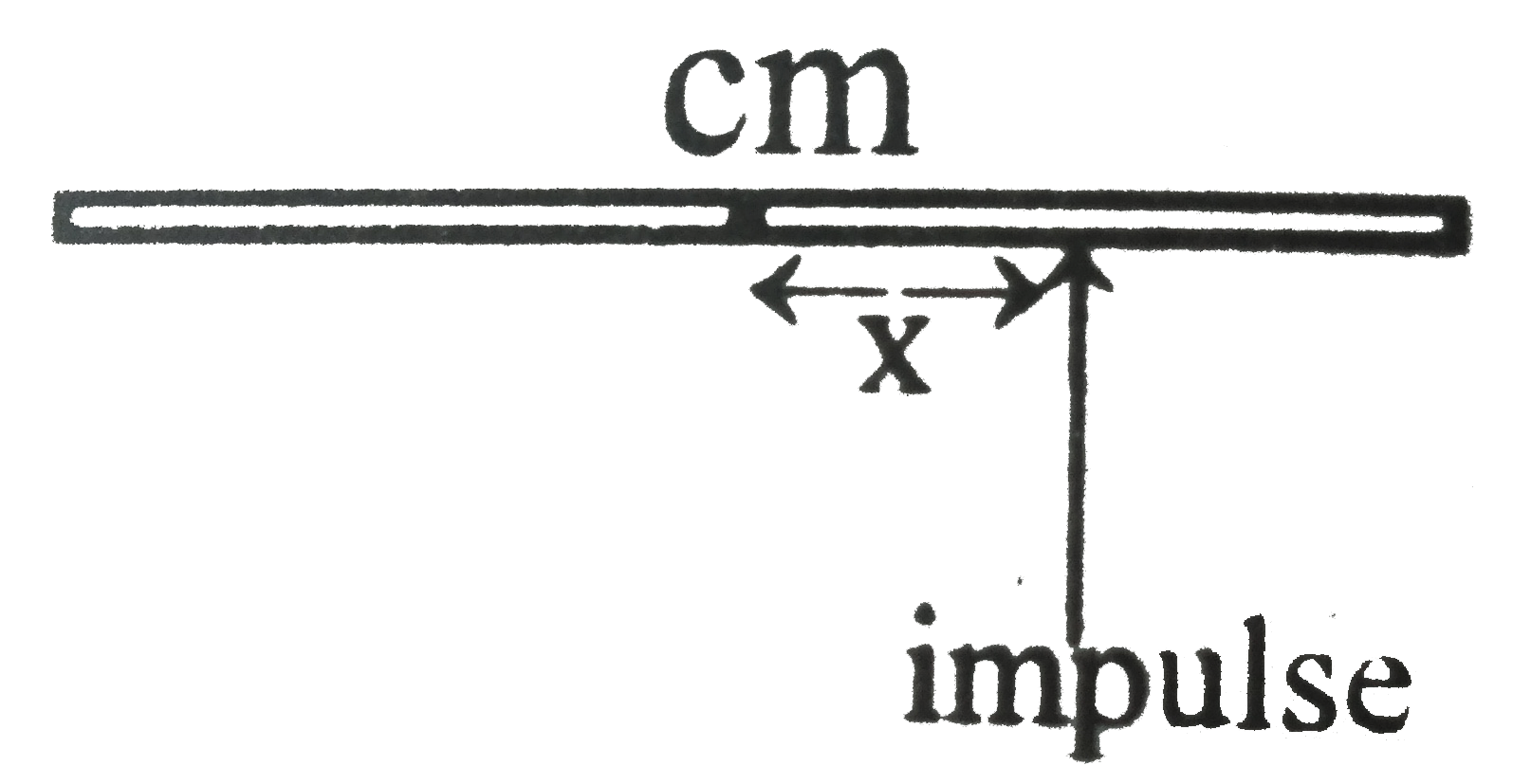 .
.
View SolutionThe dimensions of lKA are (l is the length of rod, K is the thermal conductivity of rod and A is the area of cross-section of rod)
View SolutionThe area of cross-section of rod is given by A=A0(1+αx) where A0 & α are constant and x is the distance from one end. If the thermal conductivity of the material is K. What is the thermal resistancy of the rod if its length is l0?
View Solution

