The area of cross-section of rod is given by A=A0(1+αx) where A0 & α are constant and x is the distance from one end. If the thermal conductivity of the material is K. What is the thermal resistancy of the rod if its length is l0?
KA0αln(1+αl0)
1KA0αln(1+αl0)
αKA0αln(1+αl0)
KA0αln(1+αl0)
The correct Answer is:B
dRH=dxKA=dxKA0(1+αx)
RH=∫dRH=t∫0dxKA0(1+αx)=1KA0(ln(1+αx)α)t0
=1KA0αln(1+αl0)
_E01_028_S01.png)
OR
Check dimensionally
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -02
Explore 82 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -03
Explore 11 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:SOME WORKED OUT EXAMPLES
Explore 84 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 427 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
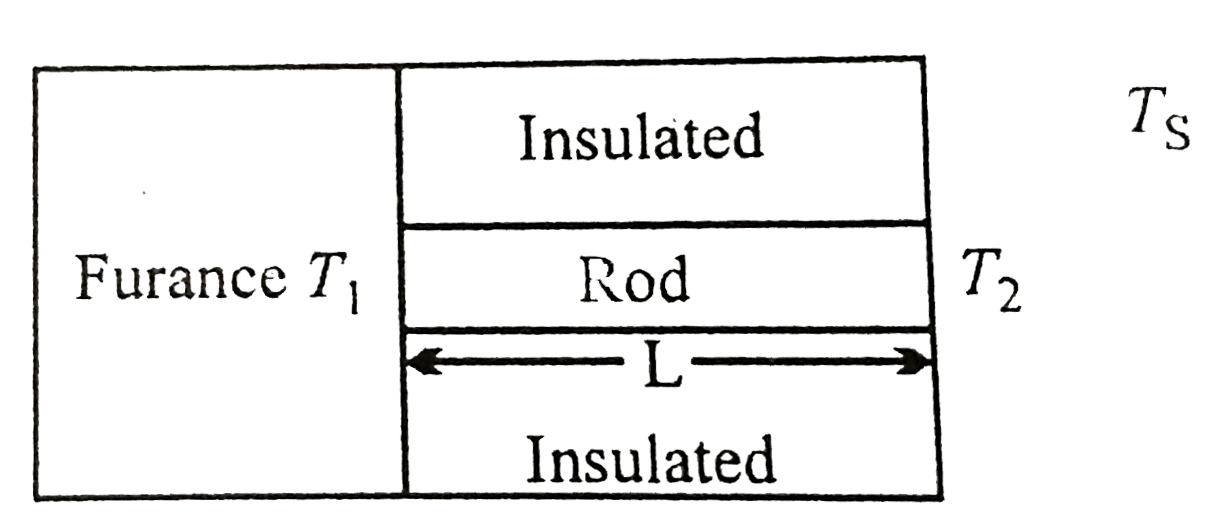
View Solution
Knowledge Check
If l is the length, A is the area of cross-section and K the thermal conductivity, then the thermal resistance of the block is given by
AKlABlKACAKlDAKlA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLThe mass per unit length of a non-uniform rod of length L is given by μ=λ×2, where λ is a constant and x is distance from one end of the rod. The distance of the center of mass of rod from this end is :-
AL2BL4C3L4DL3
The ratio of thermal conductivity of two rods of different materials is "5:4. The two rods of same area and same thermal resistance will have lengths in the ratio :-
View SolutionThe ratio of the areas of cross-section of two rods of different materials is 1:2, and the ratio of the thermal conductivities of their materials is 4:3. On keeping equal temperature-difference between the ends of these rods, the rate of conduction of heat are equal. Determine the ratio of the lengths of the rods.
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View SolutionThe dimensions of lKA are (l is the length of rod, K is the thermal conductivity of rod and A is the area of cross-section of rod)
View SolutionAssertion : If thermal conductivity of a rod is 5, then its thermal resistively is 0.2
Reason : Thermal conductivity
=1thermal resistivity
View Solution

