A long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
Current density j=iπ(R∘−r2)
Current through the smaller cross section
i'=jπr2 (in absence of cavity)
Magnetic field due to this current at a point on the axis of bigger
cylinder
B1=μ0i'2πd=μ02πd×jπr2=(μ0)×iπ(R∘−r2)
Let B2 be the magnetic field due to remaining portion. Then
B1+B2=0orB2==−B1 or |B2|=|B1|
∴B2=μ0i2πd×r2R2−r2
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
The figure shows a long cylinder and its cross section. There are N (N is a large number) wire on the curved surface of the cylinder at uniform spacing and paral- lel to its axis. Each wire has current I and cross sectional radius of wires are small compared to radius R of the cyl- inder. Find magnetic field at a distance x from the axis of the cylinder for (a)x<R (b) x>R

View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View Solution
Knowledge Check
A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
AE=14π∈0K⋅qr2BE=12π∈0k⋅qrLCE=σ/∈0kDnone of theseA long straight wire of circular cross- section carries a current along its length. On the axis inside the wire, it follows that
Astrength of electric and magnetic fields are zeroBstrength of electric field is zero but magnetic field is non− zeroCstrength of electric and magnetic field non−zeroDstrength of electric field is non−zero but magnetic field is zero.A current i is uniformly distributed over the cross section of a long hollow cylinderical wire of inner radius R1 and outer radius R2. Magnetic field B varies with distance r form the axis of the cylinder is
A B
B C
C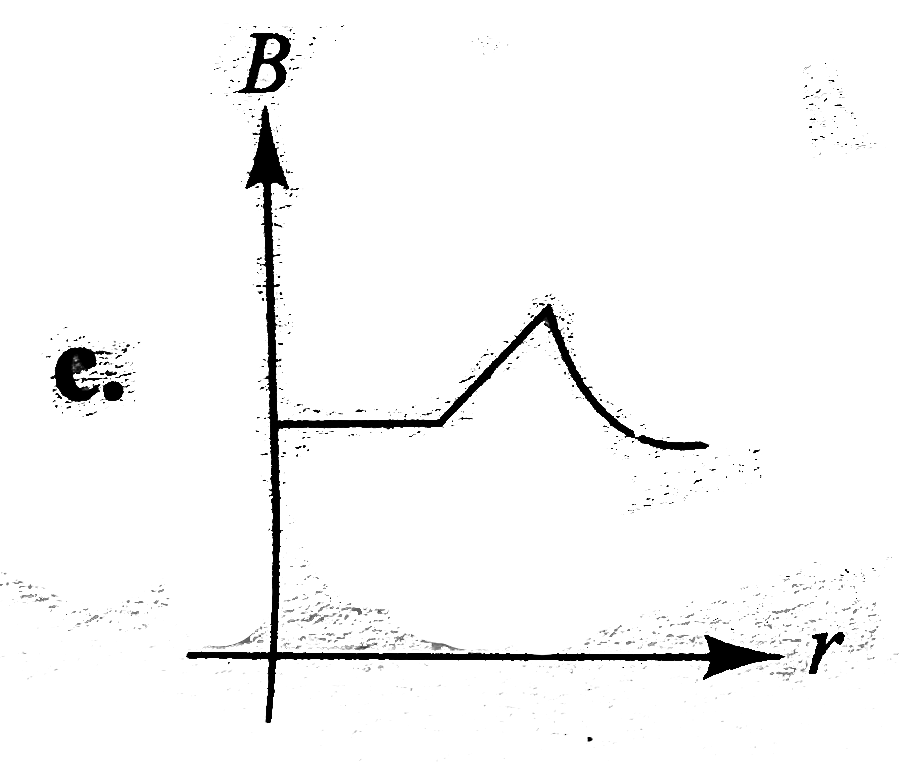 D
D
What is moment of inertia of a solid cylinder of mass m, length l and radiusr about the axis of the cylinder ?
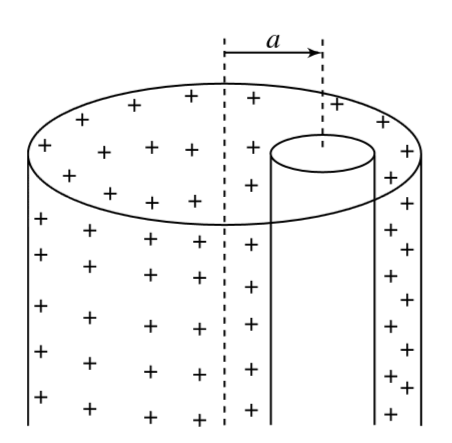
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
View SolutionCalculate the moment of inertia of a hollow cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder?
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis

View SolutionThe moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View Solution
