(a). Find the magnetic field B at point O (centre) of
(i). ABCD, which is a square of side l.
(ii). ABC, which is an equilateral triangle of side l.
(b) Twelve uniform wires of equal length l and each of resistance r are connected to form a skelton cube. A battary of emf E is connected between two diagonally opposite corners of the cube. The magnetic induction at the centreof the cube is .........
(c) An infinately long straight wire is placed at the origin along the z-axis. The current I flows along the positive z-axis. Find the unit vecotrs showing the direction of magnetic field at the four points:

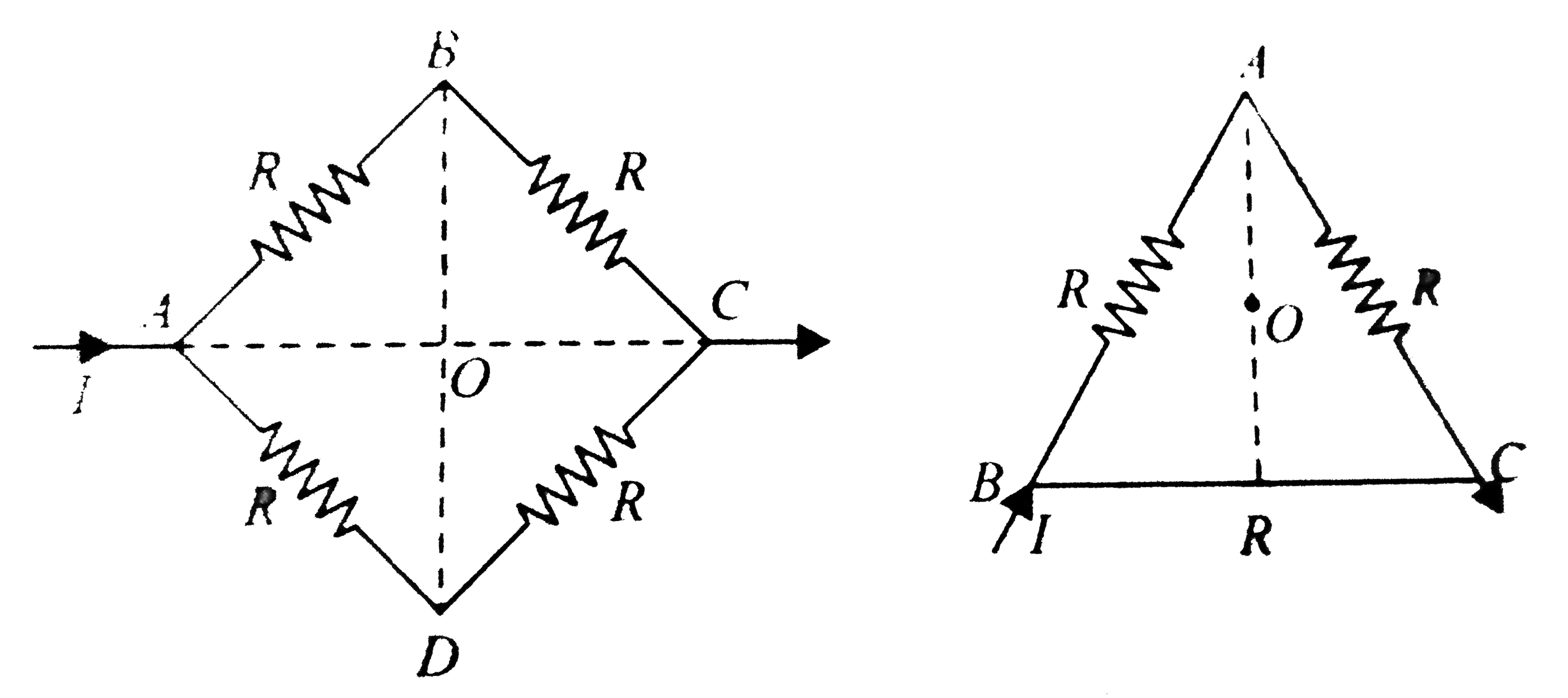
(a) i. Magnetic field due to the upper tow branches will
cancel out that due to lower branch and will be zero at
centre.
(ii) Magnetic field due to the upper two branches will cancel
out the magnetic field due to the lower branch.
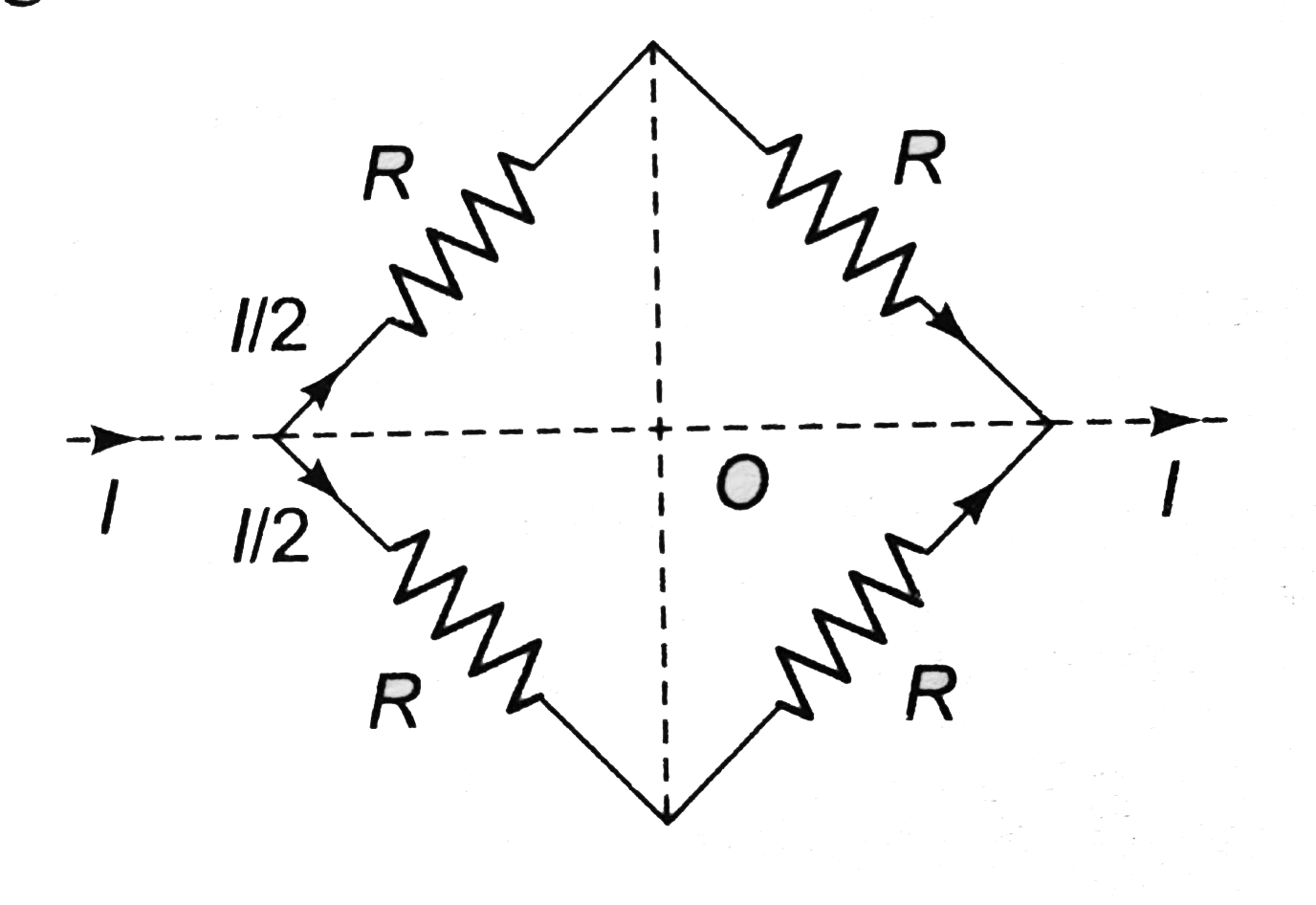
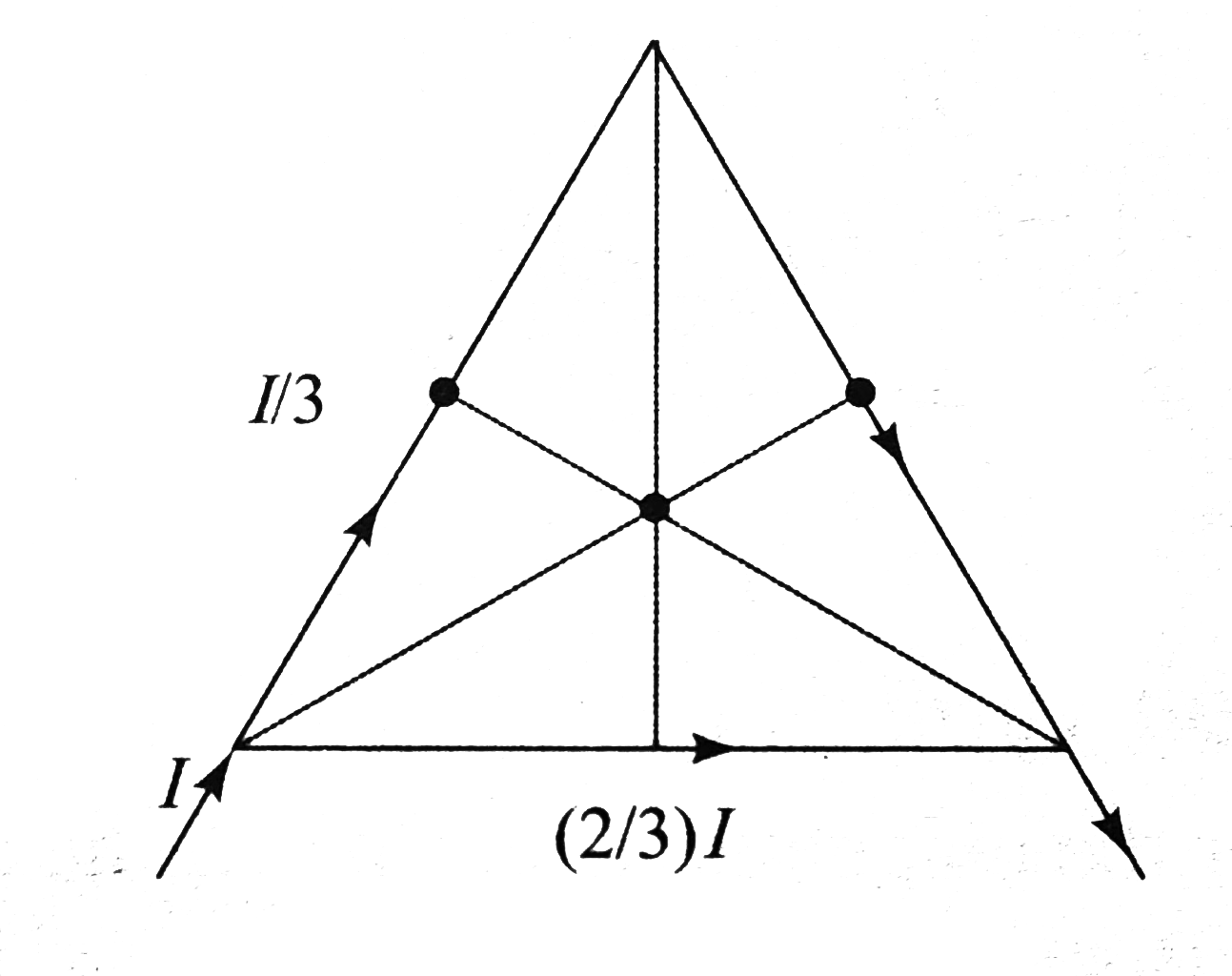
(b) Magnetic field due to each pair of wire will cancel out. Net
magnetic field will be zero.
(c) 
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Twelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View Solution
Knowledge Check
Twelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
A6ΩB12ΩC5ΩD10ΩFour wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
A5 ohmB10 ohmC20 ohmD5/4 ohmFour conductors of same resistance connected to form a square. If the resistance between diagonally opposite corners is 8 ohm, the resistance between any two adjacent corners is
A32 ohmB8 ohmC16 ohmD6 ohm
[" Four wires of equal length and of "],[" resistances "10" ohms each are "],[" connected in the form of a square."],[" The equivalent resistance between "],[" two opposite corners of the square is "]
View SolutionFour conductors of same resistance connected to form a square. If the resistance between diagonally opposite corners is 8ohm, the resistive between any two adjacent corners is
View SolutionTwelve wires, each of resistance 1Ω are connected to form a skeleton cube. Battery of 10V and neglibible internal resistance is connected across diagonally opposite corners of the cube. Determine the equivalent resistance of the network and current supplied by the battery.
View SolutionTwelve wires of equal length and same cross-section are connected in the form of a cube. If the resistance of each of the wires is R , then the effective resistance between the two diagonal ends would be

View SolutionThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
View Solution
