A coil of radius R carries current i1. Another concentric coil of radius r(r<<R) carries current i2. Planes of two coils are mutually perpendicular and both the coil are free to rotate about common diametre. Find maximum kinetic energy of smaller coil when both the coils are released, masses of coils are M and m, respectively.
Magnetic induction at centre due to current in
larger coil is
B=μ0i12R
Magnetic dipole moment of smaller coil
M=πr2i2
Initially M and B are at 90∘
So, U1=−MBcos90∘=0
when the coils become coplanar
U2=−MBcos0∘=−MB
Decrease in potential energy =U1−U2=MB=μ0i1i2πr22R
This decrease in potential energy convert into kinetic energy.
Here the kinetic energies are maximum when the coils become
coplanar. The two coils rotate due to their mutual interaction
only and if one coil rotates clockwise, then the other coil rotates
anticlockwise.
Let ω1andω2 be the angular velocities of larger and smaller coils
when they become coplanar. According to law of conservation of angular momentum,
I1ω1=I2ω2
and according to law of conservation of energy
12I1ω21+12I2ω22=U
From above two equations, we get
12I1(I2ω2I1)2+12I2ω22=U⇒12I1ω22(I1I2+1))=U
⇒12I1ω22=UI1I1+I2
So maximum kinetic energy of smaller coil is given by
⇒12I1ω22=(μ0i1i2πr22R)((1/2)MR2(1/2)MR2+(1/2)mr2)
μ0i1i2πr2MR2(MR2+mr2)
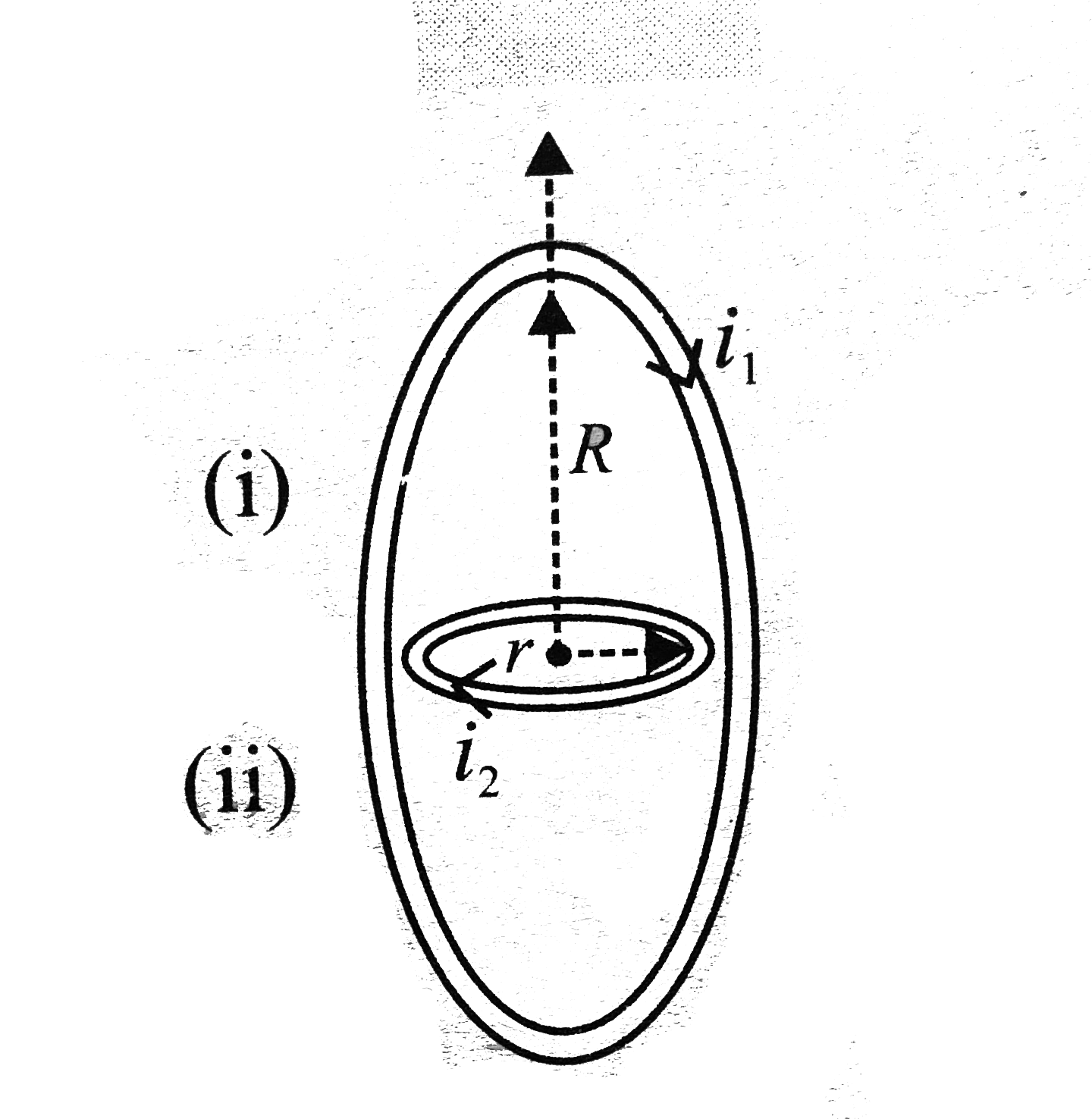
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.1
35 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
A coil of radius R carries a current i1. Another concentric coil of radius r(r<<R) carries a current i2. Planes of two coils are mutually perpendicular and both the coils are free to rotate about common diameter. Find maximum kinetic energy attained by the two coils, when both are released from rest. The masses of two coils are M and m respectively.
Strategy : The magnetic field due to coil of radius R is μ0i12R. This field exerts a torque on shorter coil. An equal and opposite torque is exerted by the shorter coil on larger coil. There is no external torque acting on the system. The angular momentum remains conserved. Also the total mechanical energy remains conserved. At any instant, let ω1andω2 represent the angular velocity
View SolutionA small coil of radius r is placed at the centre of another coaxial coil of radius R(R>>r) find the coeffcient for this pair of coils.
View Solution
Knowledge Check
A coil of radius R carries a current I. Another concentric coil of radius r(r<<R) carries current 12. Initially planes of the two coils are mutually prependicular and both the coil are free to rotate about common diameter. They are released from rest from this position. The masses of the coils are M and m respectively. (m<M). During the subsequeny motion let K1 and K2 be the maximum kinetic energies of the two cells respectively. and let U be the magnetic of maximum potential energy of magnetic interaction of the system of the coils. Choose the correct options.
AK1K2=Mm(Rr)2BK1=Umr2mr2+MR2K2=UMR2mr2+MR2CU=μ0πl2r24RDK2>>K1A coil of length L, carries a current i. The magnetic moment of coil is proportional to
ALBL2CL−1DL−2A small coil of radius r is placed at the centre of a large coil of radius R, where R>>r. The two coils are coplanar. The mutual inductance between the coils is proportional to
Ar/RBr2/RCr2/R2Dr/R2
Figure shows a larger horizontal coil of radius R carrying a current I. Another small coil of radius r(r<<R) carrying a current i & N turns is placed at the centre with its plane at an angle θ from the axis. Find the torque experienced by the smaller coil in this situation.
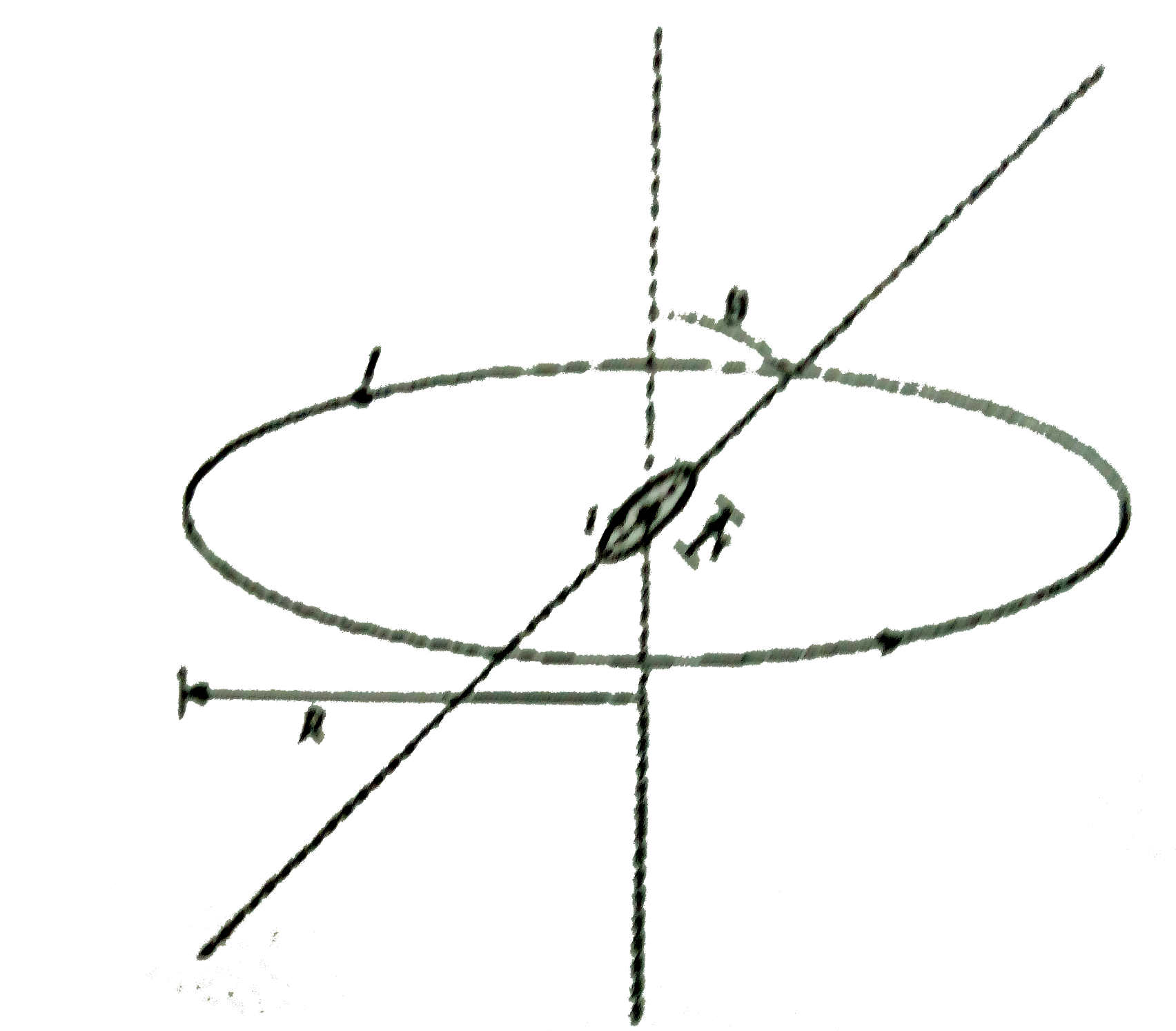
View SolutionA small coil of radius r is placed at the center of a large coil of radius R, where R>>r. The two coils are coplanar. The mutual inductance between the coils is proportional to
View SolutionA 50 mH coil carries a current of 2 A. The energy stored in the coil is
View SolutionA 200 turn closely wound circular coil of radius 15 cm carries a current of 4 A. The magnetic moment of this coil is
View SolutionA circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
View Solution
