In the given figure, two elastic rods P and Q are rigidly joined to end supports. A small mass m is moving with velocity v between the rods. All collisions are assumed to be elastic and the surface is given to be smooth. The time period of small mass m will be (A=area of cross section, Y=Young's modulus, L=length of each rod)
2Lv+2π√mLAY
2Lv+2π√2mLAY
2Lv+π√mLAY
2Lv
Rod behaves as spring constant YAl
Equivalent system is
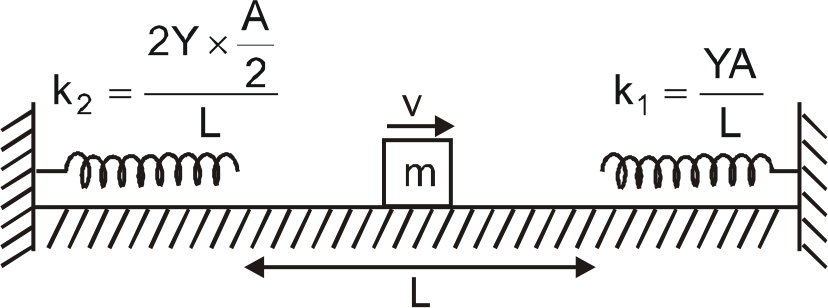
The time period of oscillations of block is
T=2LV+12(2π√mLYA)+12(2π√mL2Y.A/2)
=2LV+2π(mLAY)
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
03:22View SolutionWhen p−n junction diode is forward biased then
08:18View SolutionIn the given figure, two elastic rods P and Q are rigidly joined to end supports. A small mass m is moving with velocity v between the rods. All collisions are assumed to be elastic and the surface is given to be smooth. The time period of small mass m will be (A=area of cross section, Y=Young's modulus, L=length of each rod)
11:28View SolutionA rod PQ of mass, area of cross section A, length l and young's modulus of elasticity Y is lying on a smooth table as shown in figure. A force F is applied at P. Find
(a) tension at a distance x from end P,
(b) longitudinal stress at this point,
(c) total change in length and
(d) total strain the rod.
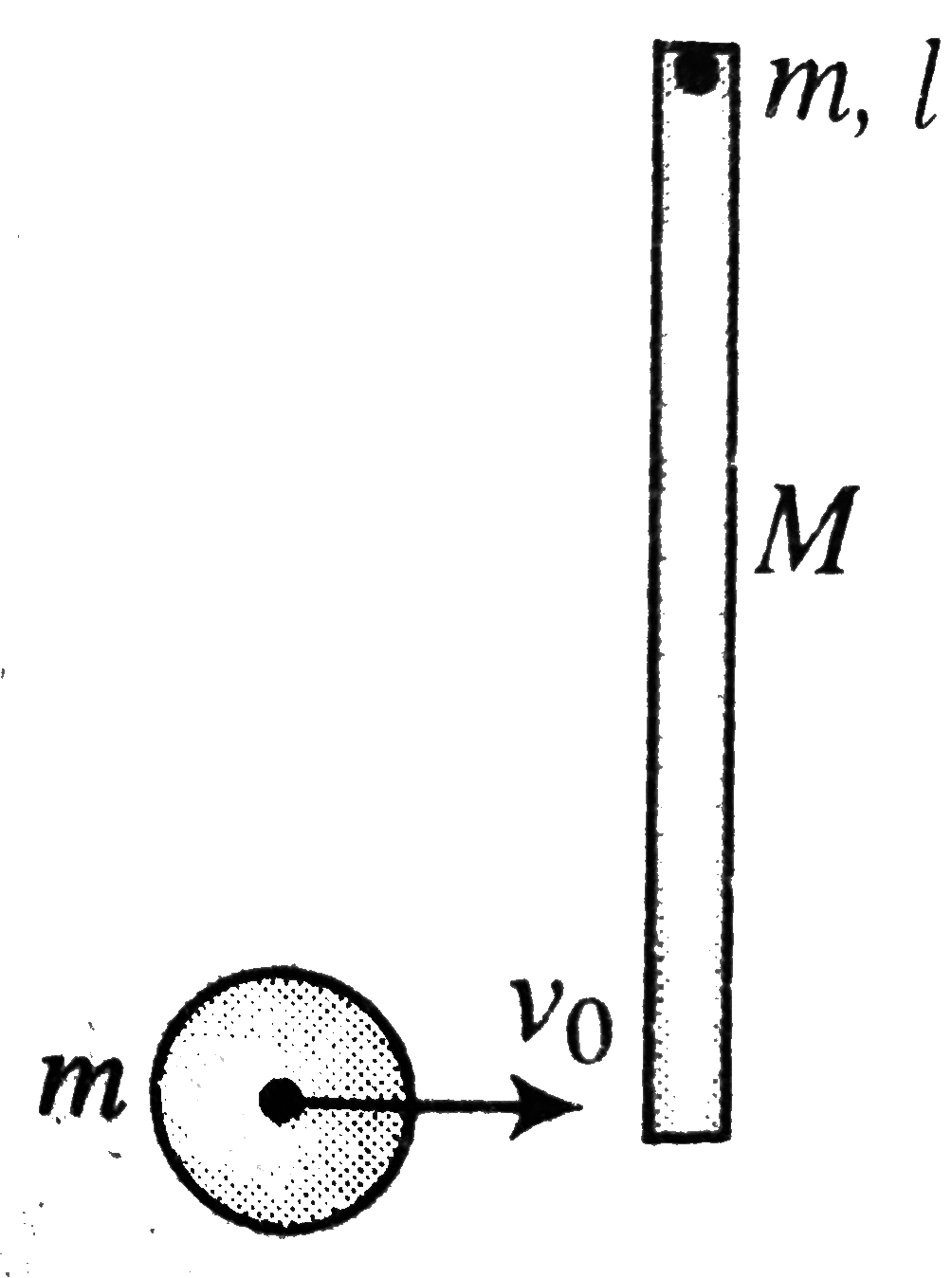
06:32View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
10:20View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l/3 from the end of the rod is instantaneously at rest just after the elastic collision?
03:55View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.04:10View SolutionA uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
02:58View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram Ratio of elastic potential energy stored in section PQ and section QR of the rod is
05:24View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram
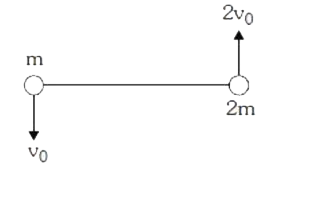
Total elastic potential energy stored in the rod is :09:07View SolutionTwo point masses of mass m and 2m placed on smooth horizontal plane are connected by a light rod of length l. Masses are given velocities in horizontal plane perpendicular to rod as shown. If area of cross section of rod is A and Young's modulus is Y, then elongation in the rod, will be
02:32View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
02:32View SolutionA mass .m. is attached with rod as shown in figture. This mass is slightly stretched and released then find the time period. (Y is Young.s modulus of rod, A is cross sectional area of rod, .l. is its length).
04:39View SolutionA mass .m. is attached with rod as shown in figture. This mass is slightly stretched and released then find the time period. (Y is Young.s modulus of rod, A is cross sectional area of rod, .l. is its length).
05:14View SolutionIn the given figure, two elastic rods P and Q are rigidly joined to end supports. A small mass m is moving with velocity v between the rods. All collisions are assumed to be elastic and the surface is given to be smooth. The time period of small mass m will be (A=area of cross section, Y=Young's modulus, L=length of each rod)
12:06View SolutionA rod PQ of mass, area of cross section A, length l and young's modulus of elasticity Y is lying on a smooth table as shown in figure. A force Fis applied at P. Find
(a) tension at a distance x from end P,
(b) longitudinal stress at this point,
(c) total change in length and
(d) total strain the rod.04:44View Solution