A uniform ring having mass m, radius R, cross section area of the wire A and young’s modulus Y is rotating with an angular speed ω(ω is small) on a smooth horizontal surface. Which of the following options is correct :
Tension in the wire is mRω22π
Change in length of the wire is mR2ω22A.Y
Change in radius of the ring is mR2ω22πA.Y
elastic potential energy stored is 14π(m2ω4R3A.Y)
Let T be the tension in the string
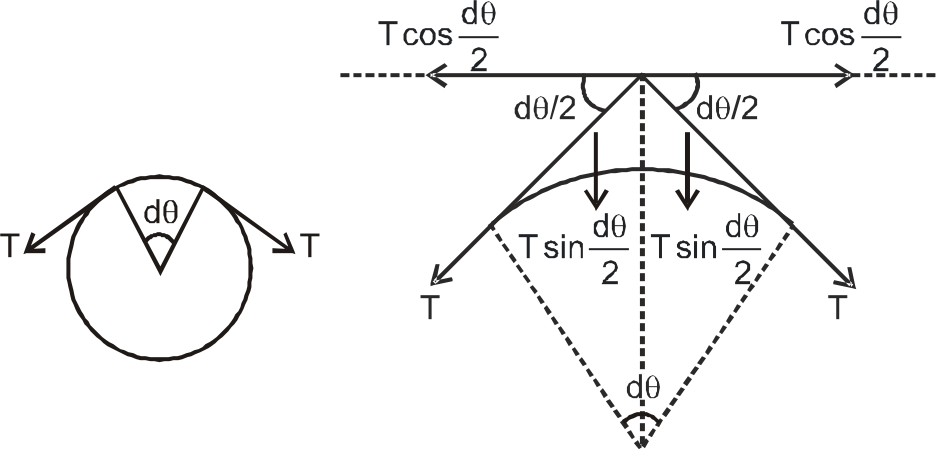
2Tsin(dθ)2=m2πR×R.ω2.Rdθ
T=mRω22π
Y=T/AΔl/l
Δll=TY.A⇒Δl=TY.a×l=m.Rω22π×1Y.A×2πR=mR2ω2Y.A
Δll=ΔRR=TY.A=m.Rω22πA.Y⇒ΔR=mR2ω22πA.Y
V=12K.X2=12(Y.A.l)×(Δl)2=12Y.A2πR×(m.R2ω2Y.A)2=14π(m2R3ω4Y.A)
Topper's Solved these Questions
Similar Questions
A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View Solution
Knowledge Check
A unifrom metallic ring of mass m, radisus R, cross sectional area 'a' and young'/s modulus Y kis kept on a smooth cone of radius 2R and semivertex angle 45∘ as shown. [Assume that extension in the ring is small]
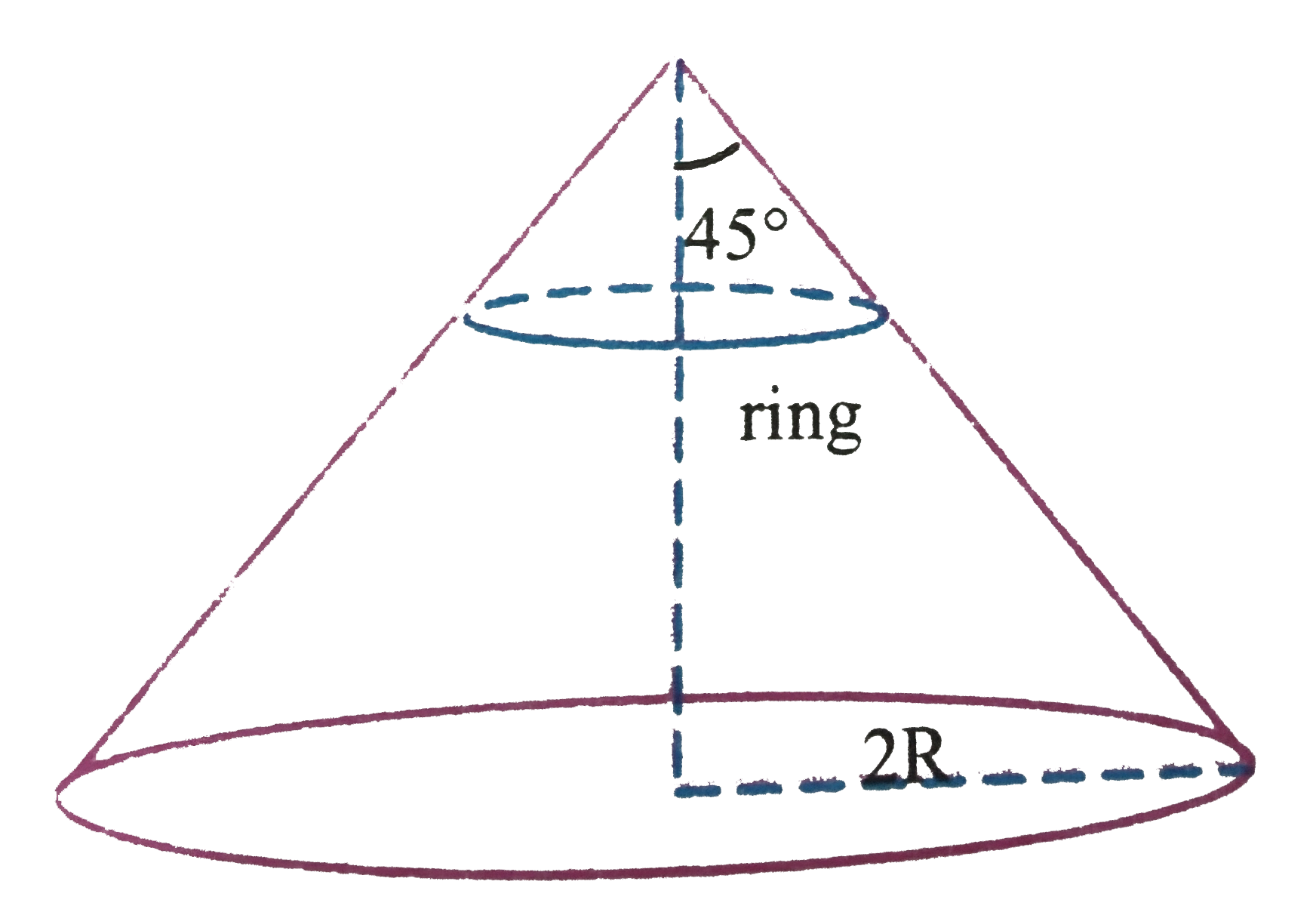 AThe tension in the ring will be same through outBThe tension in the ring will be independent of radius of ring.CThe extension in the ring will be mgRaYDElastic potential energy should in the ring will be m2g2R8πYa
AThe tension in the ring will be same through outBThe tension in the ring will be independent of radius of ring.CThe extension in the ring will be mgRaYDElastic potential energy should in the ring will be m2g2R8πYaA uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
Amω2l23AYBmω3l33AYCmω2l34AYDmω3l23AYA smooth uniform string of natural length L0, cross-sectional area A and Young's modulus Y is pulled along its length by a force F on a horizontal smooth surface. The elastic potential energy stored in the string is
A2F2L0AYBF2L02AYCF2L02AYDF2L06AY
A smooth uniform, string of natural length l, cross-sectional area A and Young’s modulus Y is pulled along its length by a force F on a horizontal surface. Find the elastic potential energy stored in the string.
View SolutionA thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is

View SolutionA uniform wire of mass m, length L, area of cross-section A and Young's modulus Y hange from the ceiling. Its elongation under its own weight will be
View SolutionTwo cylindrical vessels, each having length 10m and area of cross-sectional area of 1m2, are filled with water and rotated with angular speed ω=20rad/s. Then, which of the following statement is correct ?
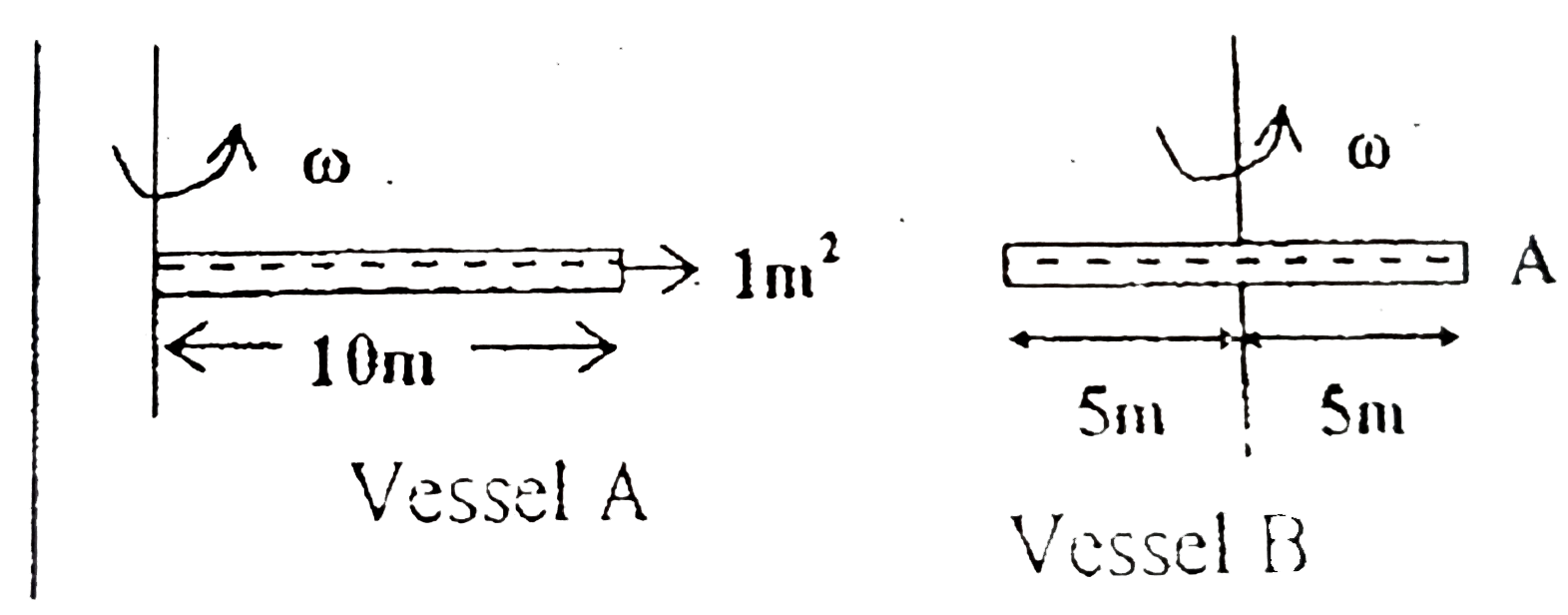
View SolutionA uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is

View Solution

