A solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

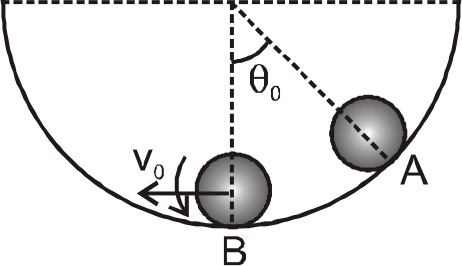
Using conservation of mechanical energy
EA=EB
mg4R(1−cosθ)=710mv20⇒8mgRsin2(θ2)=710mv20
since θ is very small
710v20=2gRθ20v20=20gR7θ20
Linear amplitude of SHM a=4Rθ0⇒θ0=a4R
v20=20gR7a216R2=528gRa2
comparing v20=ω2a2
ω=√5g28R,T=2π√28R5g
Alternate solution
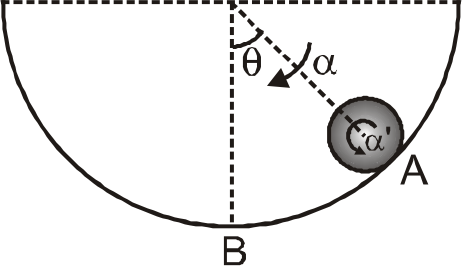
mgsinθ−fmα'R.
fR=25mR2(α')
acceleration of centre of the mass of solid sphere =α'R=α4R
solving above 3 equations ⇒mgsinθ=285mαR
For small θ
α=5gθ28R
ω=√5g28R,T=2π√28R5g
Topper's Solved these Questions
Similar Questions
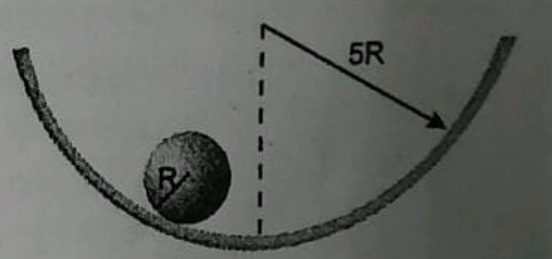
A solid sphere of (radius =R) rolls without slipping in a cylindrical vessel (radius =5R). Find the time period of small of oscillations of the sphere in s−1. Take R=114m and g=10m/s2. (axis is cylinder is fixed and horizontal).
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

View Solution
Knowledge Check
A small solid sphere of radius r rolls down an incline without slipping which ends into a vertical loop of radius R. Find the height above the base so that it just loops the loop
A52RB52(R−r)C2510(R−r)D2710R−17r10A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
A75gsinθB27gsinθC37gsinθD57gsinθ
A semi cylindrical shell with negligible thickness oscillates without slipping on a horizontal surface. The time period of small oscillations is R
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA small block oscillates back and forth on a smooth concave surface of radius R. Find the time period of small oscillation.

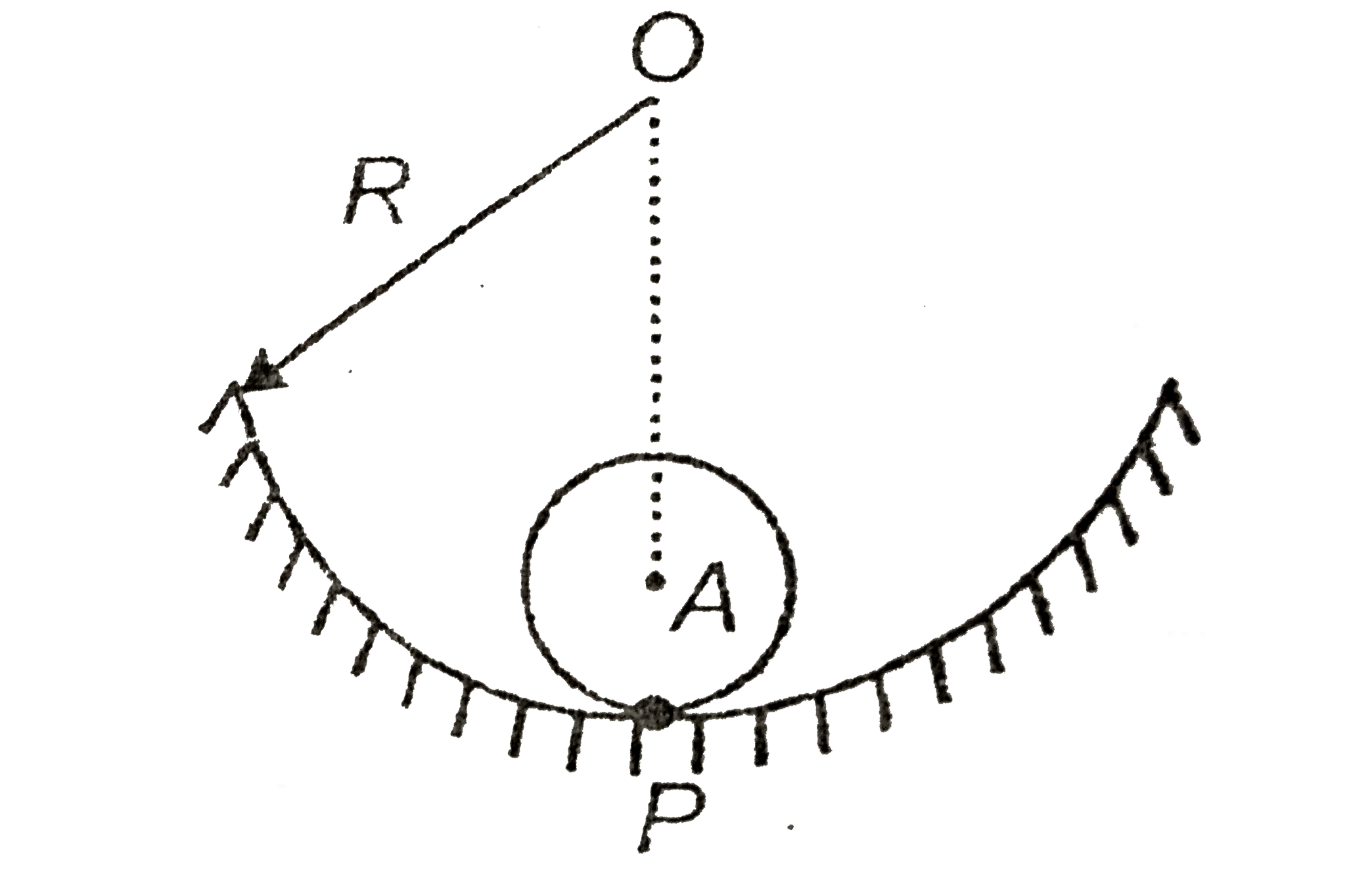
View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
View SolutionA ball of radius r is made to oscillate in a bowl of radius R, find its time period of oscillation.
View Solution

