There are two ideal springs of force constants K1 and K2 respectively. When both springs are relaxed the separation between free ends is L. Now the particle of mass m attached to free end of left spring is displaced by distance 2L towards left and then released. assuming the surface to be frictionless. (K1K2=43). (Neglect size of the block)
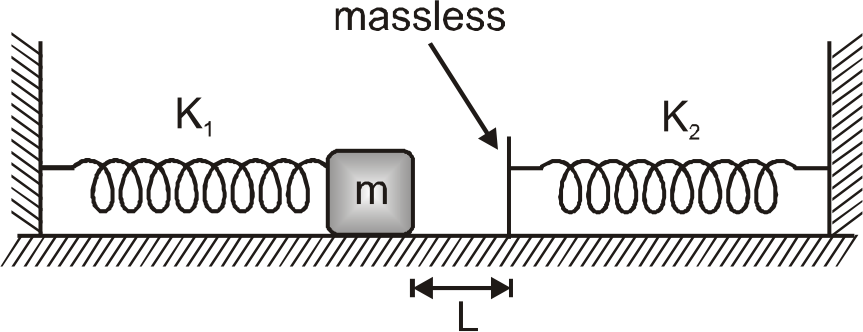
The time interval after which mass 'm' hits the right spring will be
7π6√mK1
4π3√mK1
3π4√mK1
7π4√mK1
Time taken by particle to go from
x=0 to x=A/2 is T/12
∴ time interval =T2+T12=7T12
=712.2π√mK1=7π6√mK1
Assume, maximum compression in right spring is x. hence
12K1(2L)2=12K1(L+x)2+12K2x2
Put K2=34K1, we get x=6L7
When mass m in equilibrium both spring will be in extended state.
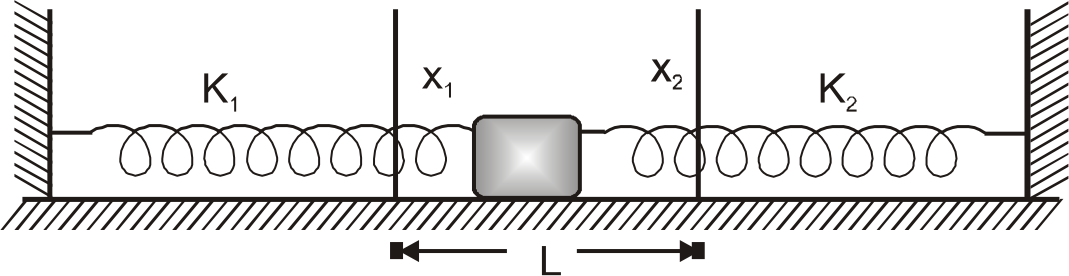
K1x1=K2x2 and x1+x2=L
x1=3L7.
Topper's Solved these Questions
Similar Questions
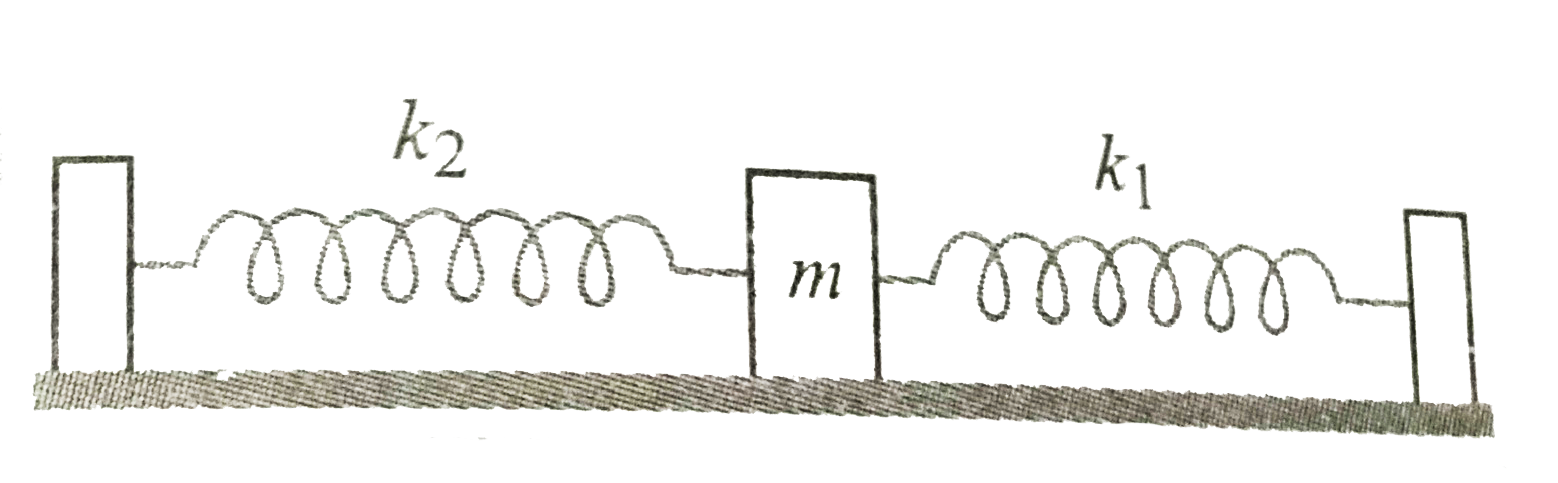
Two spring have force constants k1 and k2 respectively. They are attached to a mass m and two fixed supports as shwon in figure. If the surface is frictionless, fing the time period of oscillations. What is the spring factore of this combination.
View SolutionTwo springs have force constants kA and kB such that kB=2kA. The four ends of the springs are stretched by the same force. If energy stored in spring A is E, then energy stored in spring B is.
View Solution
Knowledge Check
There are two ideal springs of force constants K1 and K2 respectively. When both springs are relaxed the separation between free ends is L. Now the particle of mass m attached to free end of left spring is displaced by distance 2L towards left and then released. assuming the surface to be frictionless. (K1K2=43). (Neglect size of the block)

The maximum compression produced in right spring will beA6L/7B7L/6CL/3D2L/3There are two ideal springs of force constants K1 and K2 respectively. When both springs are relaxed the separation between free ends is L. Now the particle of mass m attached to free end of left spring is displaced by distance 2L towards left and then released. assuming the surface to be frictionless. (K1K2=43). (Neglect size of the block)
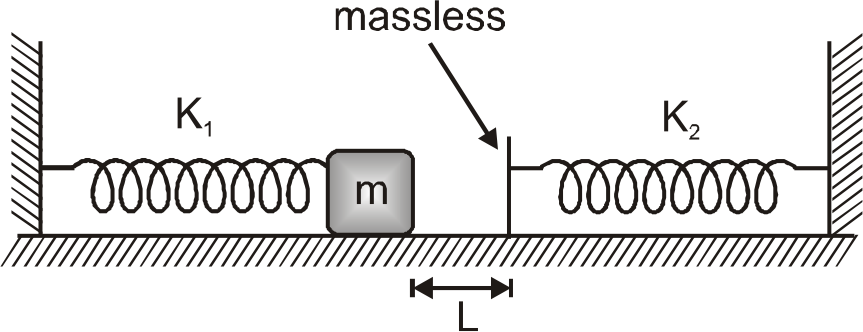
Suppose mass m hits the right spring and sticks to it. The extension in left spring when mass ‘m’ is in equilibrium position during its motion is :A4L/7B3L/7CL/3DL/2A mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is
 AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg
AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg
As shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

View SolutionA flat spiral spring of force constant K is loaded with mass M and oscillates vertically with a time period T. Then the mass suspended to the free end is
View SolutionA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
View SolutionFour massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction, then the frequency of oscillation of the system is

View SolutionA flat spiral spring of force constant k is loaded with mass M and oscillate about vertical with a time period T. Then the mass suspended to the free end is
View Solution

