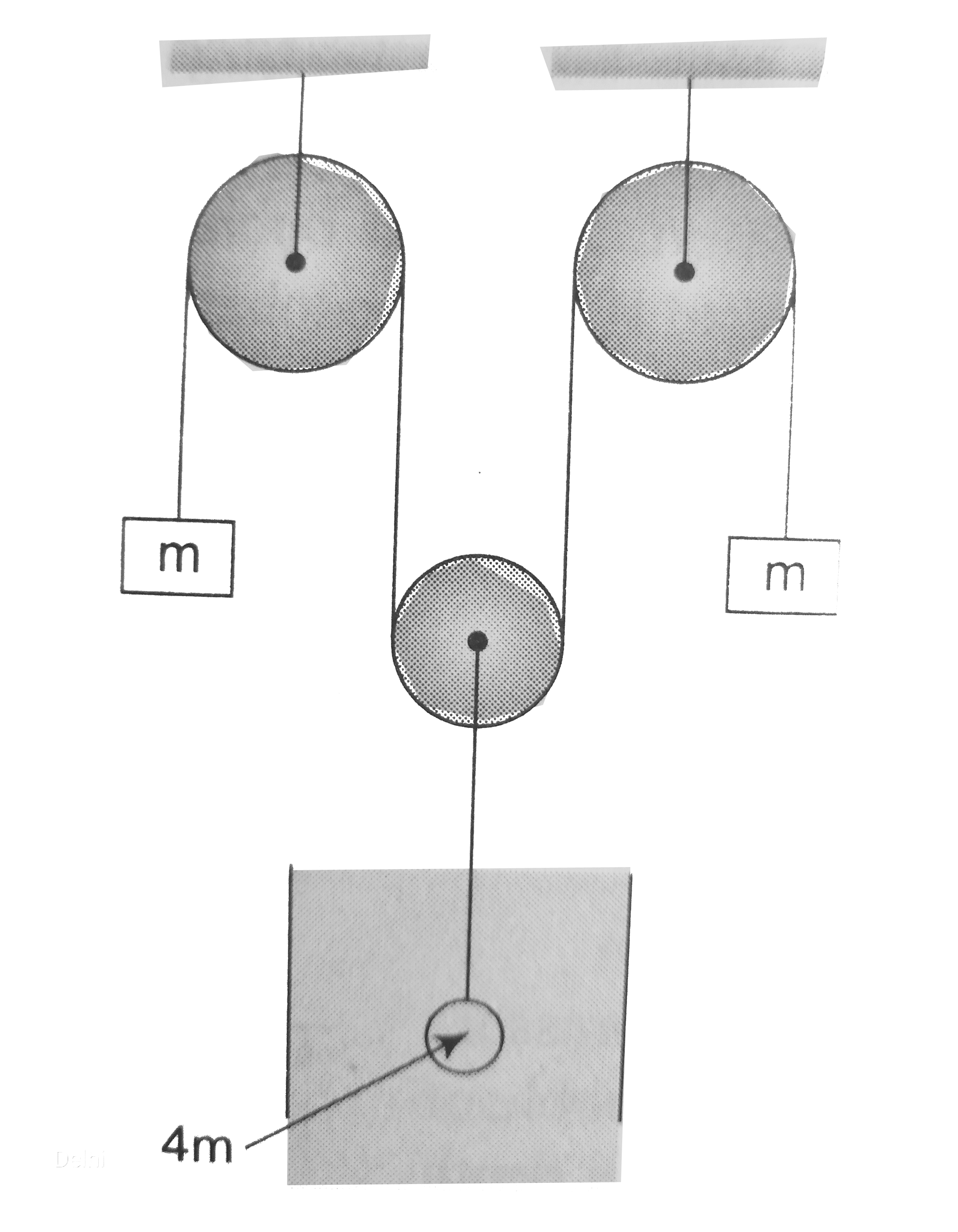
A spherical ball of mass 4m, density σ and radius r is attached to a pulley-mass system as shown in figure. The ball is released in a liquid of coefficient of viscosity η and density ρ(<σ2). If the length of the liquid column is sufficiently long, the terminal velocity attained by the ball is given by (assume all pulleys to be massless and string as massless and inextensible):
2g(r2(2σ−ρ)g)/(η)
2g(r2(σ−2ρ)g)/(η)
2g(r2(σ−4ρ)g)/(η)
1g(r2(σ−2ρ)g)/(η)
From the free body diagrame of the sphere :
Fv=4mg−2mg−FB
⇒Fv=2mg−FB
⇒6πηrV=43πr3(σ2−ρ)g
(since 4π=43πr3×σ)
⇒V=19r2(σ−2ρ)gη
Topper's Solved these Questions
Similar Questions
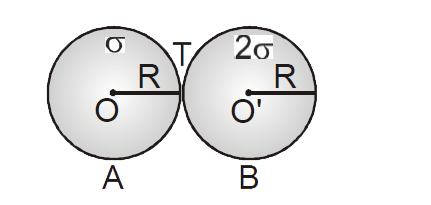
Two circular disc having radius R and mass density σ and 2σ respectively are placed as shown in figure. Then find out the position of COM of the system.
View SolutionThree masses m1,m2andm3 are attached to a string -pulley system as shown . All the three masses are held at rest and then released If m3 remains at rest , then

View Solution
Knowledge Check
A small spherical body of radius r and density ρ moves with the terminal velocity v in a fluid of coefficient of viscosity η and density σ . What will be the net force on the body?
A4π3r3(ρ−σ)gB6πηrvC0DinfinityA small steel ball of mass m and radius r is falling under gravity through a viscous liquid of coefficient of viscosity η. If g is the value of acceleration due to gravity. Then the terminal velocity of the ball is proportional to (ignore buoyancy)
Amg(η)rBmg(η)rCmgrηDmgrηA ball of mass m and radius r rolls inside a fixed hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)
.A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)
Two monkeys A and B of equal mass 'm' can climb strings of a pulley arrangement as shown in figure.Find magnitude of acceleration in m/s^(2) of A with respect to rope so that the block remains stationary.It is given that B is just holding the string.Assume pulley is frictionless and string is massless and inextensible.
View SolutionA small steel ball of radius r is allowed to fall under gravity through a column of a viscous liquid of coefficient of viscosity η. After some time the velocity of the ball attains a constant value known as terminal velocity υT. The terminal velocity depends on (i) the mass of the ball m (ii) η, (iii) r and (iv) acceleration due to gravity g . Which of the following relations is dimensionally correct?
View SolutionThe terminal velocity of a small ball falling in a viscous liquid depends upon
i) its mass m
ii) its radius r
iii) the coefficient of viscosity of the liquid η and
iv) acceleration due to gravity. Which of the following relations is dimensionally true for the terminal velocity.
View SolutionOne spherical ball of radius R, density of released in liquid of density d/2 attains a terminal velocity V. Another ball of radius 2R and density 1.5 d released in the liquid will attain a terminal velocity
View Solution
Consider a disk of mass m, radius R lying on a liquid layer of thickness T and coefficient of viscosity η as shown in the fig.

The torque required to rotate the disk at a constant angular velocity Ω given the viscosity is uniformly η.
View Solution

