As shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

k1k2
k1+k2
1k1+1k2
k1k2k1+k2
The correct Answer is:D
(d) The springs are connected in series. So, the effective force constant will be
1ke=1k1+1k2⇒ke=k1k2k1+k2
Similar Questions
Find the frequency of oscillations of the system in the figure. The bar is rigid and light.
[Hint: A spring of force constant k1 at a distance a is equivalent to a spring of force constant k1(ab)o2 at a distance b)

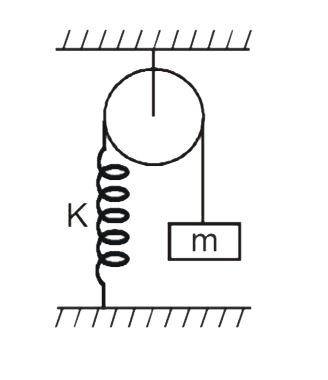
View SolutionFigure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
View Solution
Knowledge Check
Two spring of spring constant k1 and k2 are joined in series The effective spring constant of the combination is given by
A√k1k2B(k1+k2)/2Ck1+k2Dk1k2k1+k2Two springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
A√k1k2B(k1+k2)2Ck1+k2Dk1k2(k1+k2)A 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)
 AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwards
AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwards
Infinite springs with force constantk , 2k, 4k and 8 k .... respectively are connected in series. The effective force constant of the spring will b
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionIn the arrangements as shown Mgt2m. Find the extension in the spring of forces constant K1. All pulleys are smooth and massless and the blocks do not oscillates.
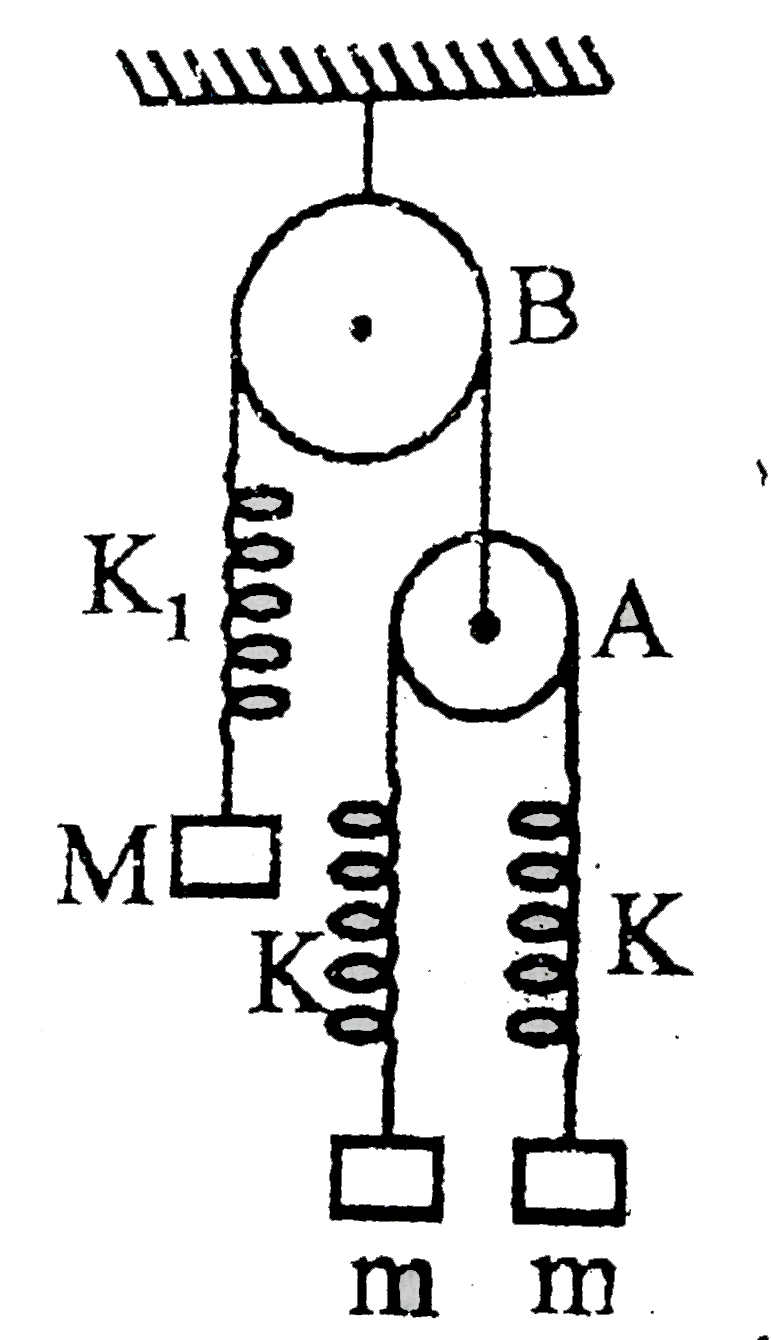
View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is

View Solution