A thin circular ring of mass per unit length p and radius r is rotating at an angular speed $ω$ as shown in figure. The tension in the ring is

A

$p ω^{2} r^{2} / 2$

B

$p ω^{2} r^{2}$

C

$p ω^{2} r^{2} / 3$

D

None

Video Solution

Text Solution

Verified by Experts

$2 T sin (\frac{d t h η}{2}) = d m R ω^{2}$
$2 T \frac{d t h η}{2} = p R D θ R ω^{2}$

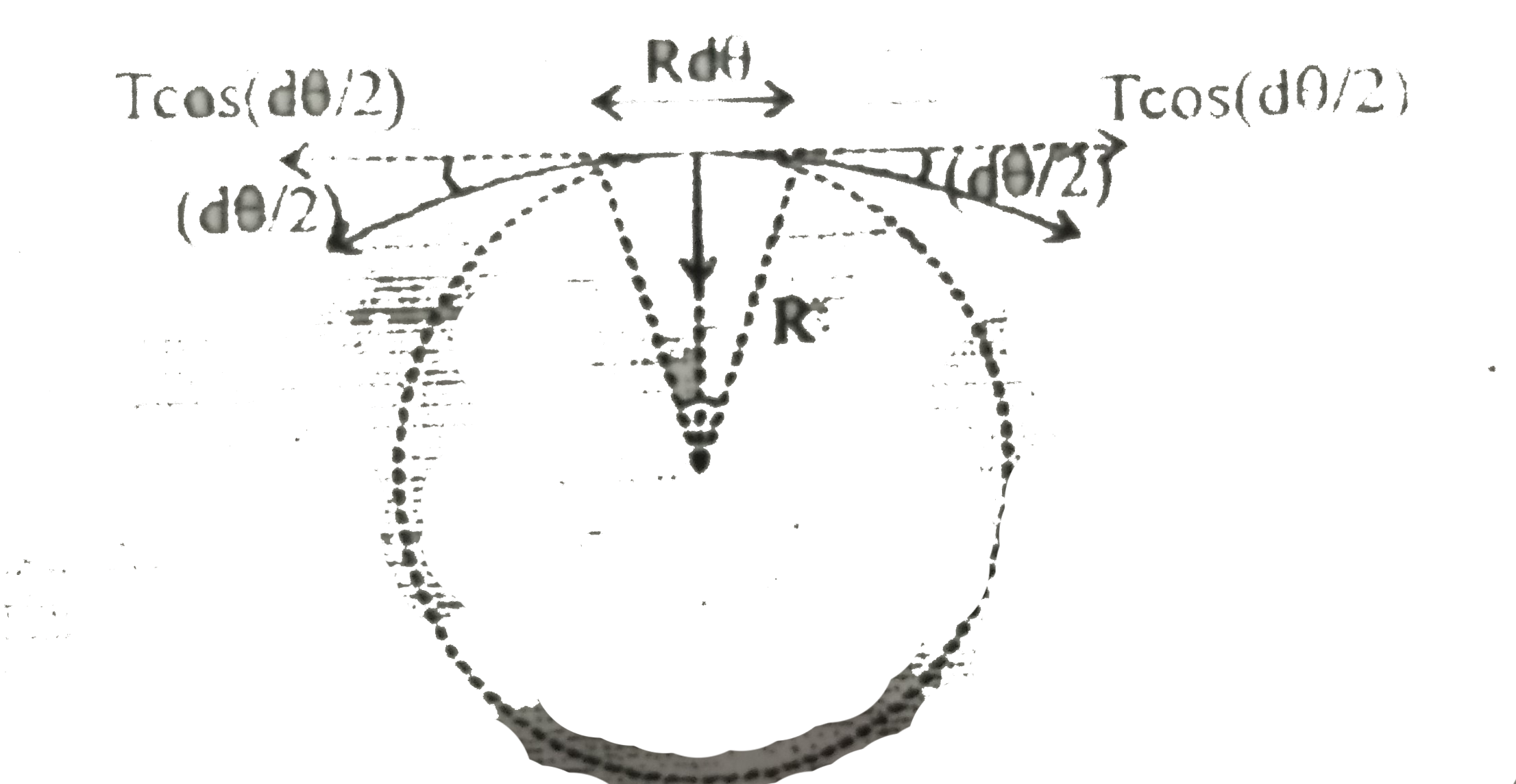
$T = p R^{2} ω^{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32videos
TEST PAPERS
BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3videos
TEST PAPERS
BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4videos
TEST PAPERS
BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32videos
SEMICONDUCTORS

Similar Questions

Knowledge Check

Question 1 - Select One
A ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity $' ω'$ in free space then :
ATension in ring is zero
BTension will vary at all points
CTension is constant throughout ring
DTension in string is $m ω^{2} r^{2}$
Question 2 - Select One
A string has a linear mass density $μ$ . The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity $ω$
Q. The tension developed in the string is
A $μ ω R^{3}$
B $2 μ ω^{2} R^{2}$
C $μ ω^{2} R^{2}$
D $μ^{2} ω^{2} R^{2}$
Question 3 - Select One
A thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity $ω$ . The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
A $\frac{ω M}{(m + M)}$
B $\frac{ω (M - 2 M)}{(M + 2 m)}$
C $\frac{ω M}{(M + 2 m)}$
D $\frac{ω (M + 2 m)}{M}$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile