A uniform rod of mass 200 grams and length L = 1m is initially at rest in vertical position. The rod is hinged at centre such that it can rotate freely without friction about a fixed horizontal axis passing through its centre. Two particles of mass m = 100 grams each having horizontal velocity of equal magnitude u = 6 m/s strike the rod at top and bottom simultaneously as shown and stick to the rod. Find the angular speed (in rad/sec.) of rod when it becomes horizontal.
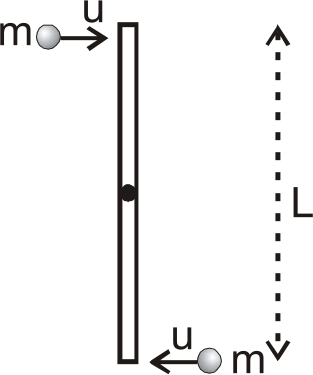
From conservation of angular momentum
muL2+muL2=[2mL212+m(L2)2+(L2)2]ω
muL=[mL26+mL24+mL24]ω=2mL23ω or ω=3u2L=3×62×1=9rad/sec
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionA uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is omega as shown in figure. calculate (a). reaction of axis at this instant, (b). Acceleration of centre of mass of the rod at this instant. (c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time. (d). minimum value of omega , so that centre of rod can complete circular motion.
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of the centre of mass of the rod is
View SolutionConsider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
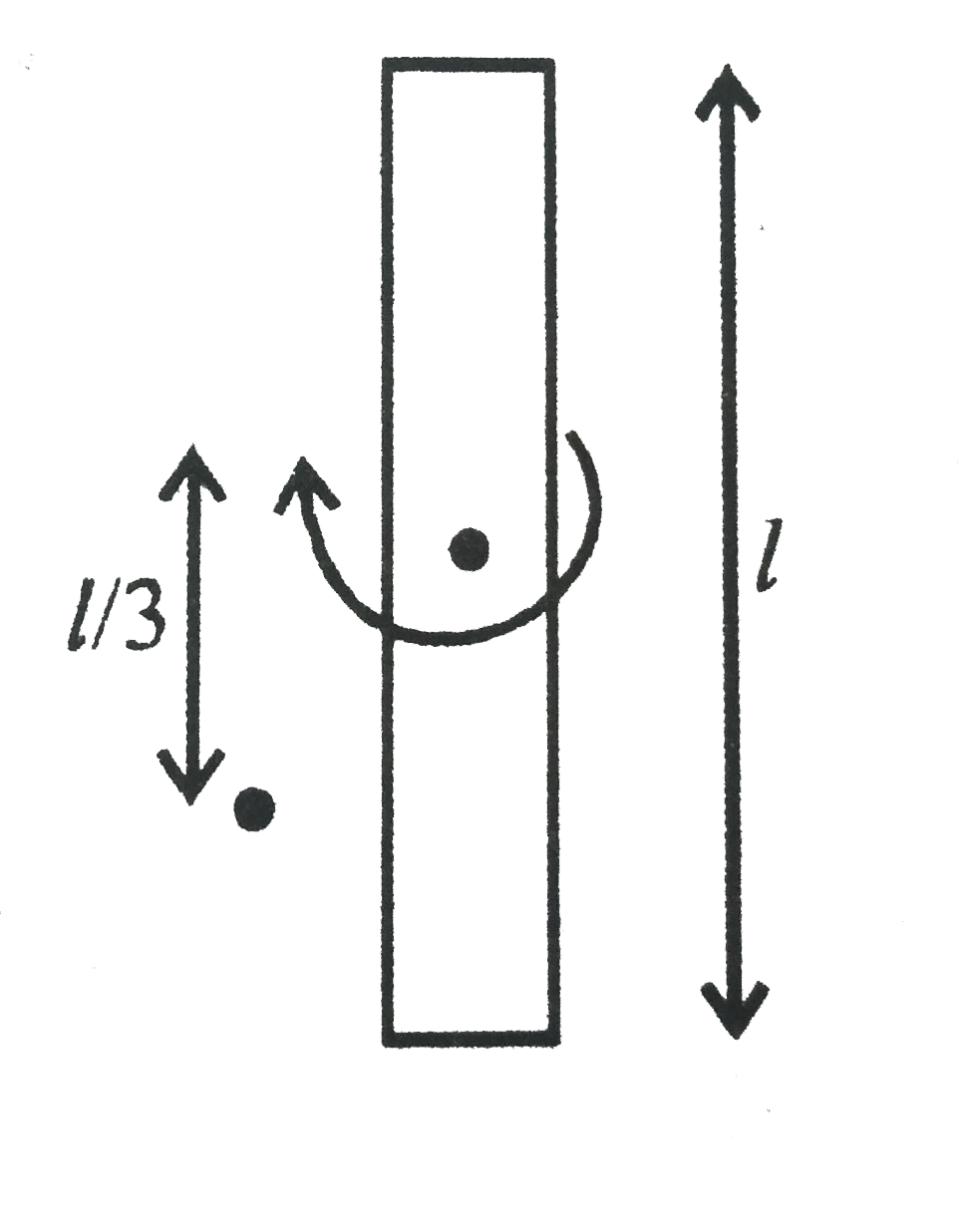
View SolutionA uniform rod of length l and mass M rotating about a fixed vertical axis on a smooth horizontal table. It elastically strikes a particle placed at a distance l/3 from its axis and stops. Mass of the particle is -
 .
.
View SolutionAB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.
View SolutionConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end. A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod

View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
View SolutionPassage - II :
Uniform rod AB hinged about a fixed point 'P' is initially vertical. Rod is released from vertical position. When rod is in horizontal position.

The acceleration of centre of mass of rod is
View SolutionA uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is omega as shown in figure. calculate (a). reaction of axis at this instant, (b). Acceleration of centre of mass of the rod at this instant. (c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time. (d). minimum value of omega , so that centre of rod can complete circular motion.
View SolutionConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of the centre of mass of the rod is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod is released from rest in the Position shown by slightly displacing it clockwise. Find the hinge reaction at the axis of rotation at the instant the rod turns through. 90^@
View Solution

