
A uniform rod of length 4l and mass m is free to rotate about a horizontal axis passing through a point distant l from its one end. When the rod is horizontal its angular velocity is ω as shown in figure. calculate
(a). reaction of axis at this instant,
(b). Acceleration of centre of mass of the rod at this instant.
(c). reaction of axis and acceleration of centre mass of the rod when rod becomes vertical for the first time.
(d). minimum value of ω, so that centre of rod can complete circular motion.
α=mglm(4l)212+ml2=37.gl
∴(aC)v=lα=37g

Let V be the vertical reaction (upwards) at axis, then
mg−V=maC=3mg7
∴V=47mg ..(i)
If H be the horizontal reaction (towards CO) at axis the
H=m/ω2 ..(ii)
∴ total reaction at axis
N=√H2+V2=47mg√1+(7lω24g)2
(b). aC=√(aC)2V+(lω2)2
=√(3g7)2+(lω2)2
(c) Let ω' be the angular speed of the rod when it becomes vertical for the first time. then from conservation of mechanical energy
12I(ω'2−ω2)=mgl
∴ω'2=ω2+2mglI
=ω2+2mgl73ml2
=ω2+67gl
Acceleration of centre of mass at this instance will be,
aC=lω'2=lω'2+6g7
Let V be the reaction (upwards) at axis at this instant, then
V−mg=maC=mlω2+6mg6
∴V=137mg+mlω2
(d). from conservation of mechanical energy
mgl=12Iω2min
∴ωmin=√2mglI=
⎷2mgl73ml2
=√67gl
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A thin uniform rod of length l and mass m is swinging freely about a horizontal axis passing through its end. Its maximum angular speed is ω. Its centre of mass rises to a maximum height of -
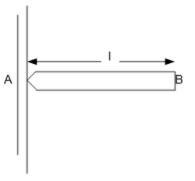
View SolutionA uniform rod AB of length l and mass m is free to rotate about an Axis passing through A and perpendicular to length of the rod. The rod is released from rest as shown in figure. Given that the moment of inertia of the rod about A is ml23 The initial angular acceleration of the rod will be
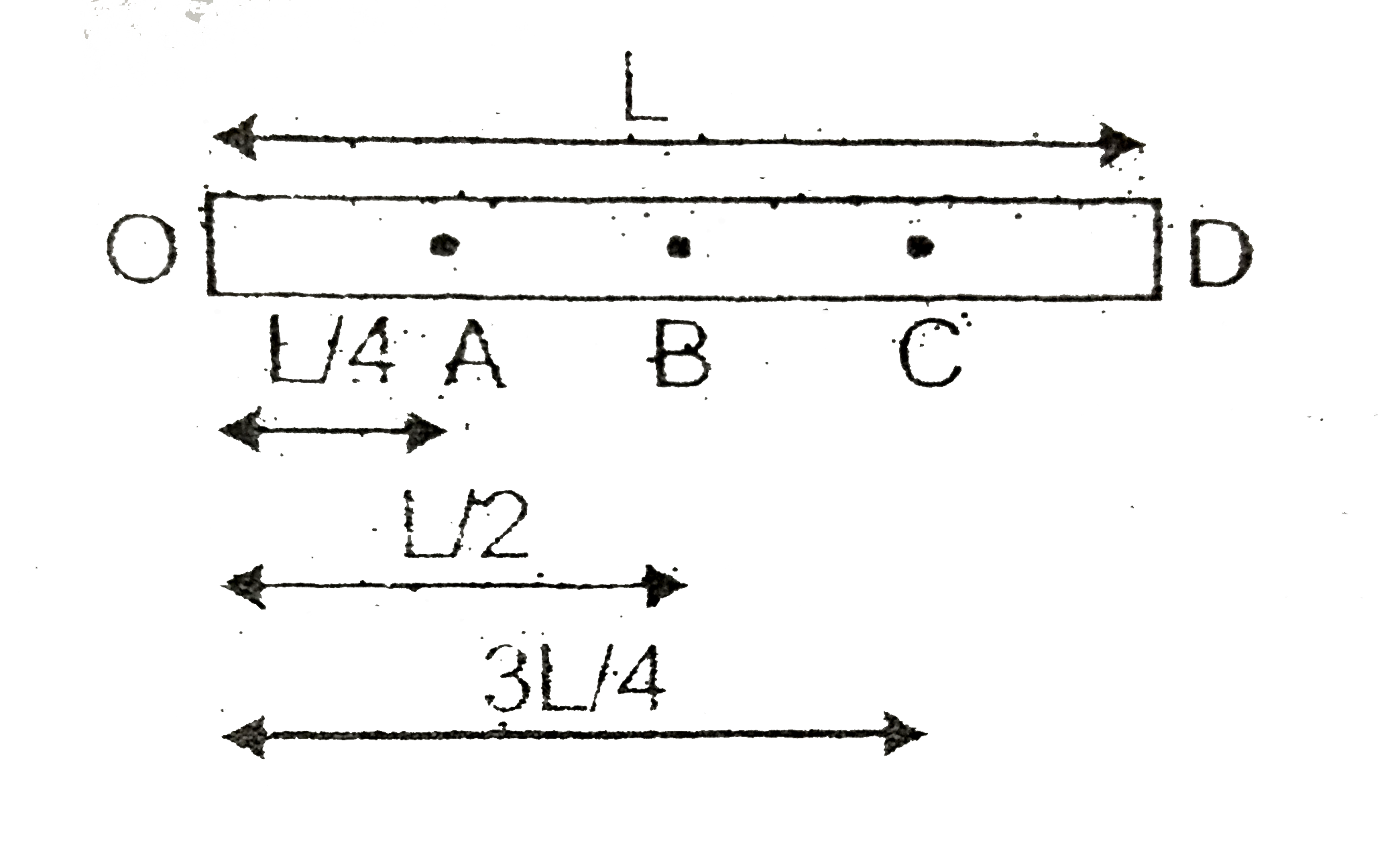
View SolutionA uniform rod of length L is free to rotate about an axis passing through O. Inititally the rod is horizontal. The rod is relased from this position. Match column I with column II
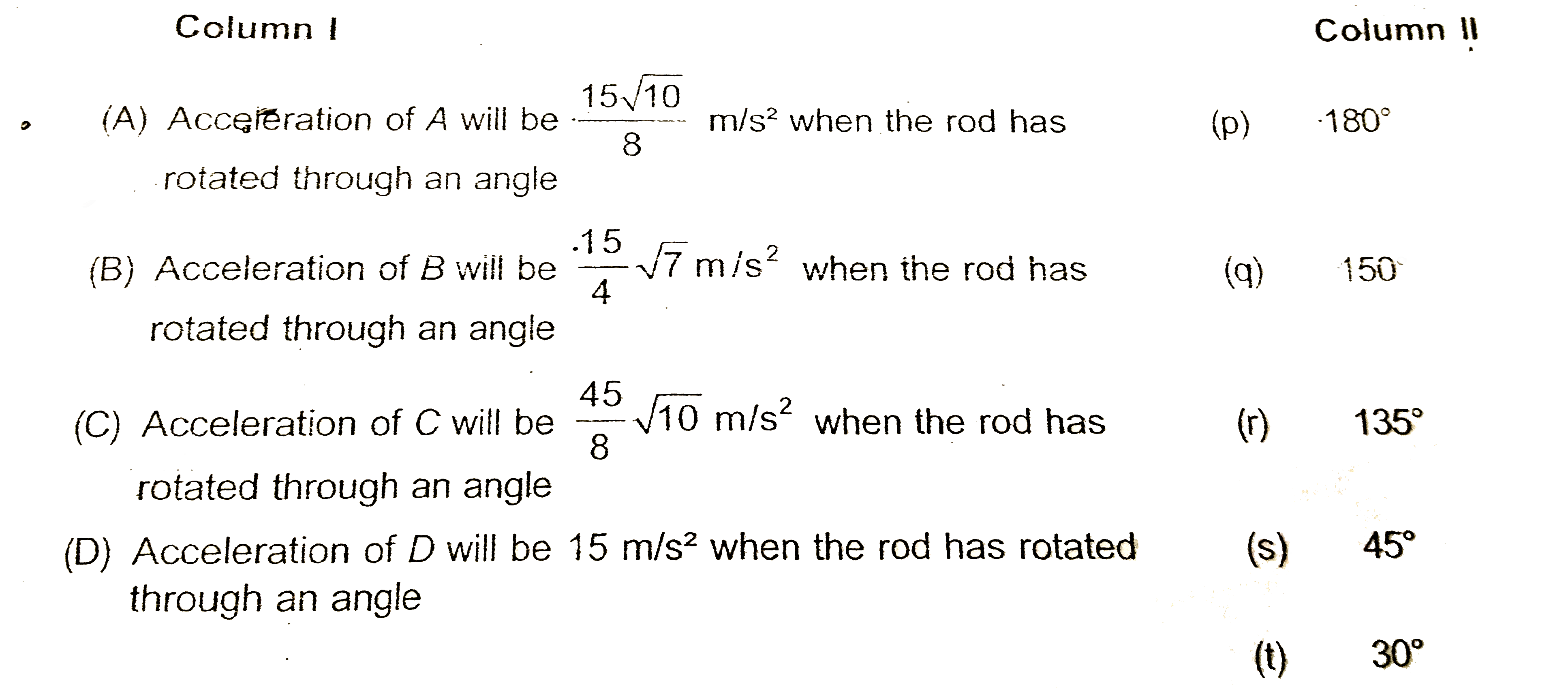
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution