A uniform stick of length and mass hinged at end is released from rest at an angle with the vertical show that when the angle with the vertical is . The hinge exerts of force along the stick and perpendicular tot he stick given by and

(i) C is the centre of mass of the rod. Let be the angular speed of rod about point O at angle . From conservation of mechanical energy.
..(i)
Now, ..(ii)
From eqs. (i) and (ii) we get
hence proved
(ii) angular acceleration of rod at this instant
Tangential acceleration of COM.
...(iii)
Now ....(iv)
from eqs. (iii) and (iv), we get
Here negative sign implies that direction of is opposite to the component .
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A uniform stick of mass M is placed in a frictionless well as shown. The stick makes an angle θ with the horizontal. Then the force which the vertical wall exerts on right end of stick is :

View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F
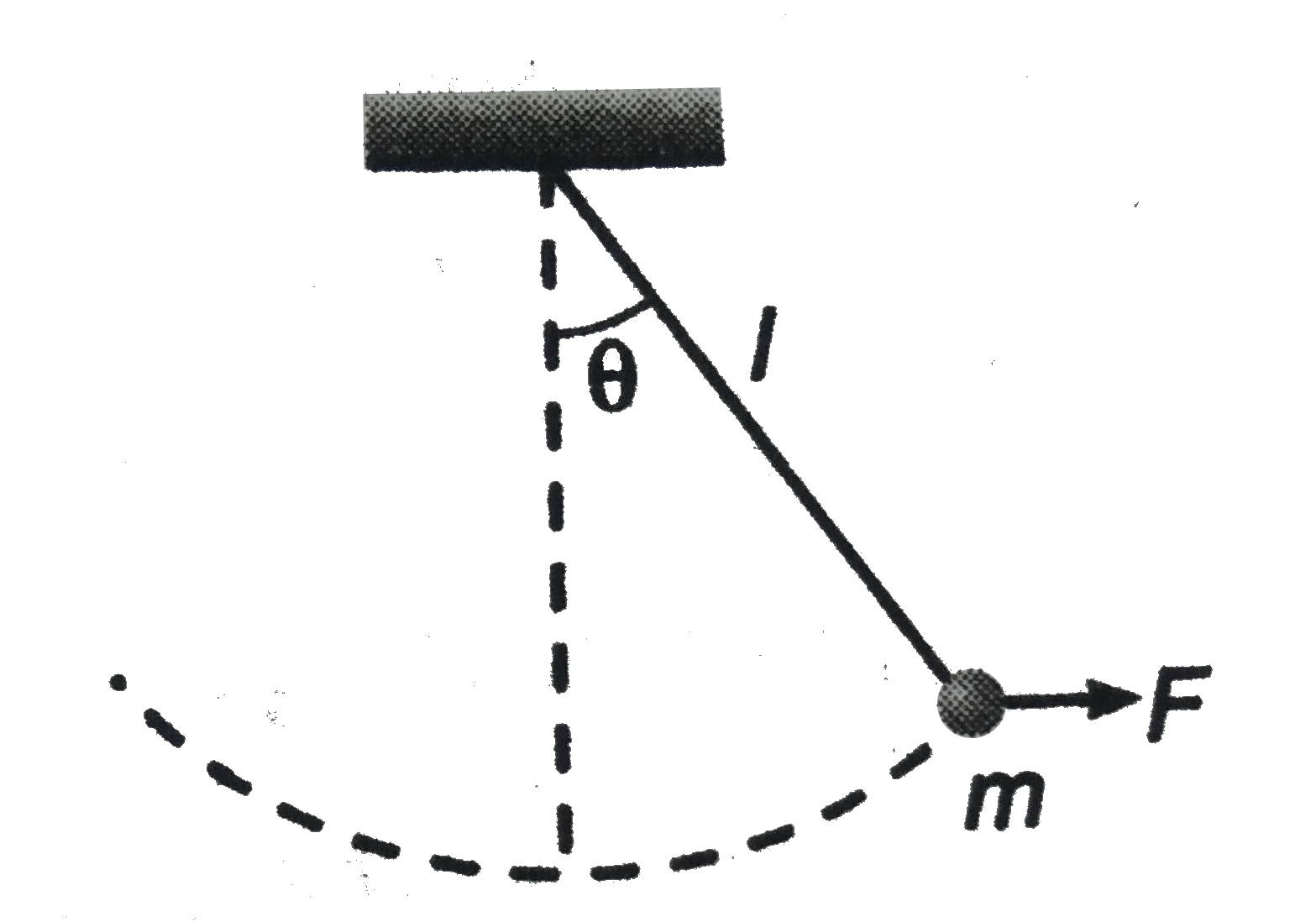 .
.
View SolutionA thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
View SolutionA uniform wooden stick of mass 1.6 kg and length l rests in an inclined mannar on a smooth, vertical wall of height h(<l) such that a small portion of the stick extends beyond the wall. The reaction force of th wall on the stick is perpendicular to the stick. The stick makes an angle of 30∘ with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio h/l and the friectional force f at the bottom of the stick are (g=10ms2)
View SolutionAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle thit θ with the vertical. Find the work done by the force F
 .
.
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
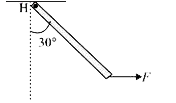
View SolutionA rod of length L and mass M is acted on by two unequal force F1andF2(<F1) as shown in the following figure.

The tension in the rod at a distance y from the end a is given by
View SolutionA mass 'M' is suspended by a rope from a rigid support. It is pulled horizontally with a force F. If the rope makes an angle ' θ' with vertical in equilibrium, then the tention in the string is
View SolutionA uniform slender rod of mass m and length L is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle θ=30∘ with the vertical. Thent he value of normal reaction from the from the floor just after release will be
View Solution
