A uniform rod AB of mass 3m and length 4l, which is free to turn in a vertical plane about a smooth horizontal axis through A, is released from rest when horizontal. When the rod first becomes vertical, a point C of the rod, where AC=3l strikes a fixed peg. Find the linear impulse exerted by the peg on the rod if
(a). The rod is brought to rest by the peg.
(b). The rod rebounds and next comes to instantaneous rest inclined to the downward vertical at an angle π3 radian.
To solve the problem, we will break it down into two parts as specified in the question:
Part (a): The rod is brought to rest by the peg.
1. Identify the system: We have a uniform rod AB of mass 3m and length 4l pivoted at point A. The center of mass of the rod is at a distance of 2l from point A.
2. Initial potential energy: When the rod is horizontal, the center of mass is at height 2l above the lowest point. The potential energy (PE) when horizontal is:
PE=3m⋅g⋅(2l)=6mgl
3. Final kinetic energy: When the rod becomes vertical, all the potential energy converts into kinetic energy (KE). The moment of inertia I of the rod about point A is given by:
I=13⋅(3m)⋅(4l)2=13⋅3m⋅16l2=16ml2
The kinetic energy when the rod is vertical is:
KE=12Iω2=12⋅16ml2⋅ω2
4. Equate potential energy to kinetic energy:
6mgl=12⋅16ml2⋅ω2
Simplifying gives:
12g=16l⋅ω2⟹ω2=12g16l=3g4l⟹ω=√3g4l
5. Calculate the angular momentum just before the impact: The angular momentum L just before the impact is:
L=Iω=16ml2⋅√3g4l=16ml2⋅√3g2√l=8ml√3g
6. Impulse-momentum theorem: The impulse J exerted by the peg is related to the change in angular momentum:
J⋅(3l)=ΔL⟹J⋅(3l)=8ml√3g
Solving for J:
J=8ml√3g3l=8m√3g3
Part (b): The rod rebounds and comes to instantaneous rest inclined at an angle π3.
1. Determine the new angular velocity after rebounding: When the rod is inclined at π3, the height of the center of mass is:
h=2l−2lcos(π3)=2l−2l⋅12=2l−l=l
The change in potential energy when it rebounds is:
ΔPE=3mgl
2. Kinetic energy at the lowest point before rebounding: The kinetic energy just before rebounding is equal to the potential energy lost:
KE=3mgl=12Iω′2
Using the moment of inertia I=16ml2:
3mgl=12⋅16ml2⋅ω′2⟹6g=16l⋅ω′2⟹ω′2=6g16l=3g8l⟹ω′=√3g8l
3. Calculate the change in angular momentum: The angular momentum after rebounding is:
L′=Iω′=16ml2⋅√3g8l=16ml2⋅√3g2√2l=8ml√6g
4. Calculate the impulse: The impulse is given by:
J⋅(3l)=L′−L
Substituting the values we found:
J⋅(3l)=8ml√6g−8ml√3g
Factoring out 8ml:
J⋅(3l)=8ml(√6g−√3g)
Solving for J:
J=8ml(√6g−√3g)3l=8m(√6g−√3g)3
Final Answers:
(a) The linear impulse exerted by the peg when the rod is brought to rest is:
J=8m√3g3
(b) The linear impulse exerted by the peg when the rod rebounds is:
J=8m(√6g−√3g)3
PE=3m⋅g⋅(2l)=6mgl
I=13⋅(3m)⋅(4l)2=13⋅3m⋅16l2=16ml2
The kinetic energy when the rod is vertical is:
KE=12Iω2=12⋅16ml2⋅ω2
6mgl=12⋅16ml2⋅ω2
Simplifying gives:
12g=16l⋅ω2⟹ω2=12g16l=3g4l⟹ω=√3g4l
L=Iω=16ml2⋅√3g4l=16ml2⋅√3g2√l=8ml√3g
J⋅(3l)=ΔL⟹J⋅(3l)=8ml√3g
Solving for J:
J=8ml√3g3l=8m√3g3
h=2l−2lcos(π3)=2l−2l⋅12=2l−l=l
The change in potential energy when it rebounds is:
ΔPE=3mgl
KE=3mgl=12Iω′2
Using the moment of inertia I=16ml2:
3mgl=12⋅16ml2⋅ω′2⟹6g=16l⋅ω′2⟹ω′2=6g16l=3g8l⟹ω′=√3g8l
L′=Iω′=16ml2⋅√3g8l=16ml2⋅√3g2√2l=8ml√6g
J⋅(3l)=L′−L
Substituting the values we found:
J⋅(3l)=8ml√6g−8ml√3g
Factoring out 8ml:
J⋅(3l)=8ml(√6g−√3g)
Solving for J:
J=8ml(√6g−√3g)3l=8m(√6g−√3g)3
(a) The linear impulse exerted by the peg when the rod is brought to rest is:
J=8m√3g3
J=8m(√6g−√3g)3
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Video
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

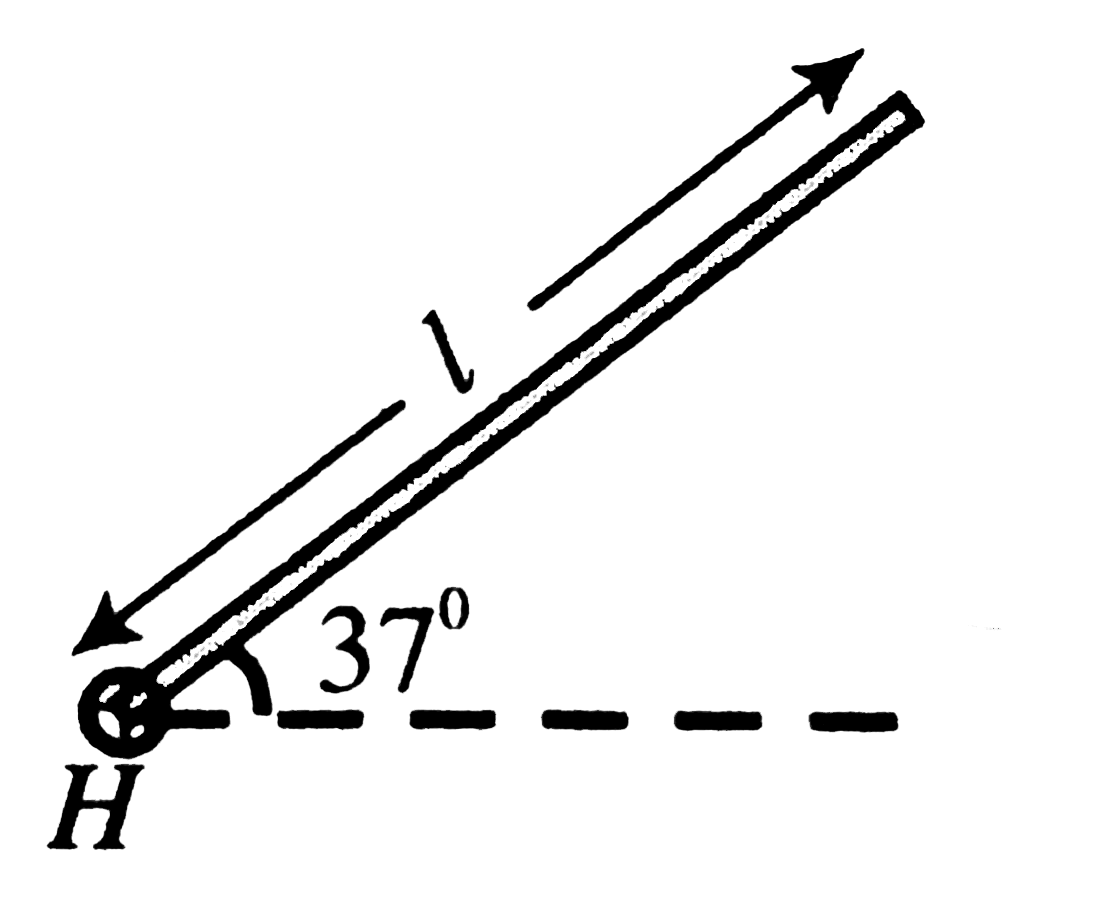
View SolutionA uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. Find angular acceleration α of the rod just after it is released from initial position making an angle of 37∘ with horizontal from rest?
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
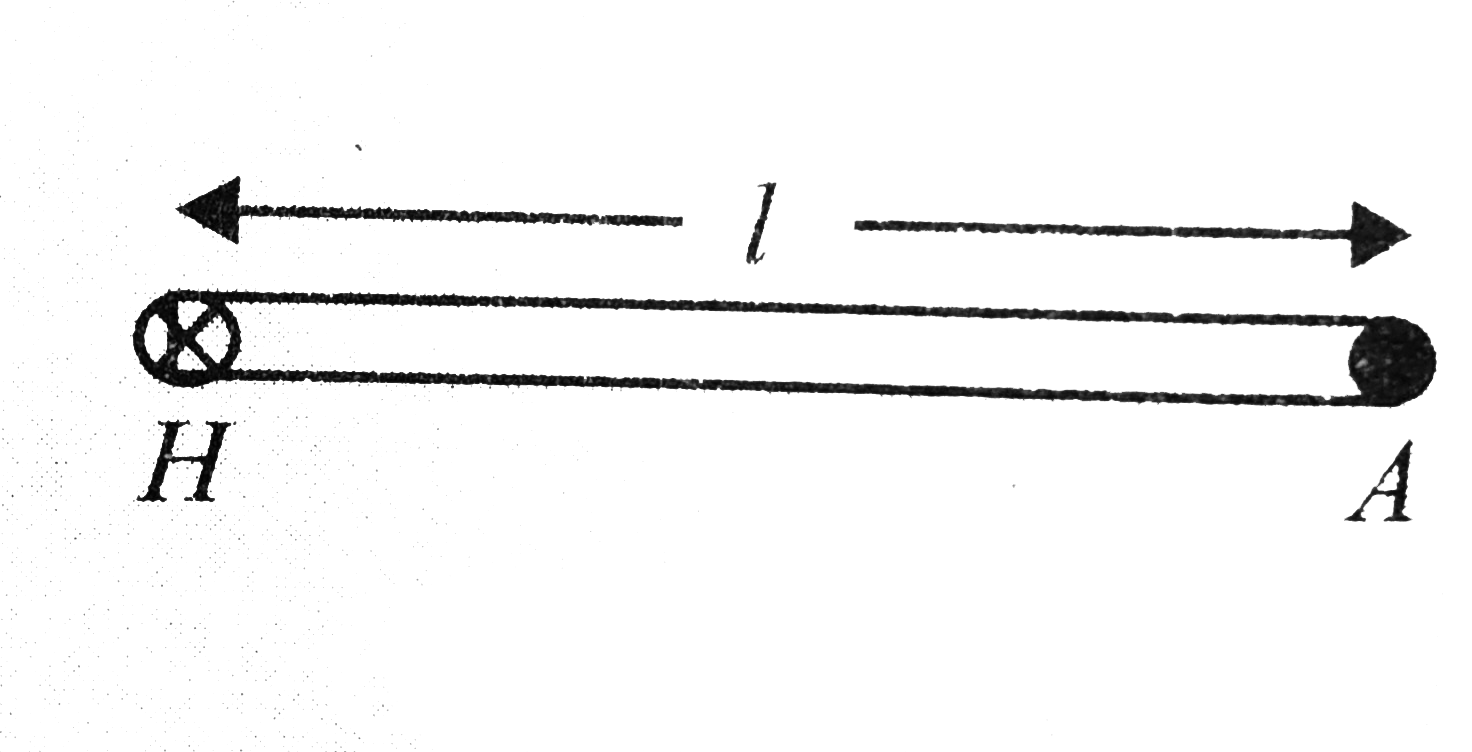
View SolutionABC is a triangular framwork of three uniform rods each of mass m and length 2l. It is free to rotate in its own plane about a smooth horizontal axis through A which is perpendicular to ABC. If it is released from rest when AB is horizontal and C is above AB. Find the maximum velocity of C in the subsequent motion.
View SolutionA slender rod of mass m and length L is pivoted about a horizontal axis through one end and released from rest at an angle of 30∘ above the horizontal. The force exerted by the pivot on the rod at the instant when the rod passes through a horizontal position is

View Solution
