ABC is a triangular framwork of three uniform rods each of mass m and length 2l. It is free to rotate in its own plane about a smooth horizontal axis through A which is perpendicular to ABC. If it is released from rest when AB is horizontal and C is above AB. Find the maximum velocity of C in the subsequent motion.
To solve the problem step by step, we will analyze the motion of the triangular framework and apply the principles of conservation of energy and rotational dynamics.
Step 1: Understand the System
We have a triangular framework ABC made of three uniform rods, each of mass m and length 2l. The framework is free to rotate about point A, which is horizontal and perpendicular to the plane of the triangle.
Step 2: Initial Configuration
When the framework is released from rest, the rod AB is horizontal, and point C is directly above AB. The initial height of the center of mass (COM) of the system can be calculated.
The height of the center of mass (COM) for a triangle formed by three equal mass rods can be found using the formula:
hCOM=h3=√3l3
where h is the height from point A to point C.
Step 3: Final Configuration
As the system rotates about point A, the height of the center of mass changes. The final height of the center of mass when the system is at its lowest point can be calculated as:
hfinal=−2√3l3
This indicates that the center of mass has fallen by:
Δh=hfinal−hinitial=−2√3l3−√3l3=−√3l
Step 4: Calculate the Loss in Potential Energy
The loss in potential energy (PE) of the system as it falls can be calculated using:
ΔPE=mghinitial−mghfinal
Substituting the heights:
ΔPE=3m⋅g⋅(√3l3)−3m⋅g⋅(−2√3l3)
=3mg⋅(√3l3+2√3l3)=3mg⋅√3l
Step 5: Calculate the Moment of Inertia
Next, we need to find the total moment of inertia I of the system about point A. The moment of inertia for each rod can be calculated using the parallel axis theorem:
- For rods AB and AC:
IAB=13m(2l)2=43ml2
IAC=43ml2
- For rod BC, using the parallel axis theorem:
IBC=13m(2l)2+m⋅(hCOM)2=43ml2+m⋅(2√3l)2=43ml2+12ml2=403ml2
Thus, the total moment of inertia is:
Itotal=IAB+IAC+IBC=43ml2+43ml2+403ml2=483ml2=16ml2
Step 6: Apply Conservation of Energy
Using the conservation of mechanical energy:
ΔPE=KE
3mg√3l=12Iω2
Substituting I:
3mg√3l=12(16ml2)ω2
Cancelling m and simplifying:
3g√3=8lω2
ω2=3g√38l
Step 7: Calculate the Maximum Velocity of C
The linear velocity v of point C can be calculated using:
v=rω
where r=2l:
v=2l⋅√3g√38l=2l⋅√3g√3√8l=2√3g√3√8l
Simplifying gives:
v=√32⋅2√3g=2√3g2
Final Answer
Thus, the maximum velocity of point C in the subsequent motion is:
v=2√3g
We have a triangular framework ABC made of three uniform rods, each of mass m and length 2l. The framework is free to rotate about point A, which is horizontal and perpendicular to the plane of the triangle.
When the framework is released from rest, the rod AB is horizontal, and point C is directly above AB. The initial height of the center of mass (COM) of the system can be calculated.
hCOM=h3=√3l3
where h is the height from point A to point C.
As the system rotates about point A, the height of the center of mass changes. The final height of the center of mass when the system is at its lowest point can be calculated as:
hfinal=−2√3l3
This indicates that the center of mass has fallen by:
Δh=hfinal−hinitial=−2√3l3−√3l3=−√3l
The loss in potential energy (PE) of the system as it falls can be calculated using:
ΔPE=mghinitial−mghfinal
Substituting the heights:
ΔPE=3m⋅g⋅(√3l3)−3m⋅g⋅(−2√3l3)
=3mg⋅(√3l3+2√3l3)=3mg⋅√3l
Next, we need to find the total moment of inertia I of the system about point A. The moment of inertia for each rod can be calculated using the parallel axis theorem:
- For rods AB and AC:
IAB=13m(2l)2=43ml2
IAC=43ml2
- For rod BC, using the parallel axis theorem:
IBC=13m(2l)2+m⋅(hCOM)2=43ml2+m⋅(2√3l)2=43ml2+12ml2=403ml2
Itotal=IAB+IAC+IBC=43ml2+43ml2+403ml2=483ml2=16ml2
Using the conservation of mechanical energy:
ΔPE=KE
3mg√3l=12Iω2
Substituting I:
3mg√3l=12(16ml2)ω2
Cancelling m and simplifying:
3g√3=8lω2
ω2=3g√38l
The linear velocity v of point C can be calculated using:
v=rω
where r=2l:
v=2l⋅√3g√38l=2l⋅√3g√3√8l=2√3g√3√8l
Simplifying gives:
v=√32⋅2√3g=2√3g2
Thus, the maximum velocity of point C in the subsequent motion is:
v=2√3g
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Video
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A uniform rod of mass m and length l can rotate in a vertical plane abota smooth horizontal axis hinged at point H. Find the force exerted by the hinge just after rod is released from rest, from initial horizontal position?

View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionA uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. Find angular acceleration α of the rod just after it is released from initial position making an angle of 37∘ with horizontal from rest?
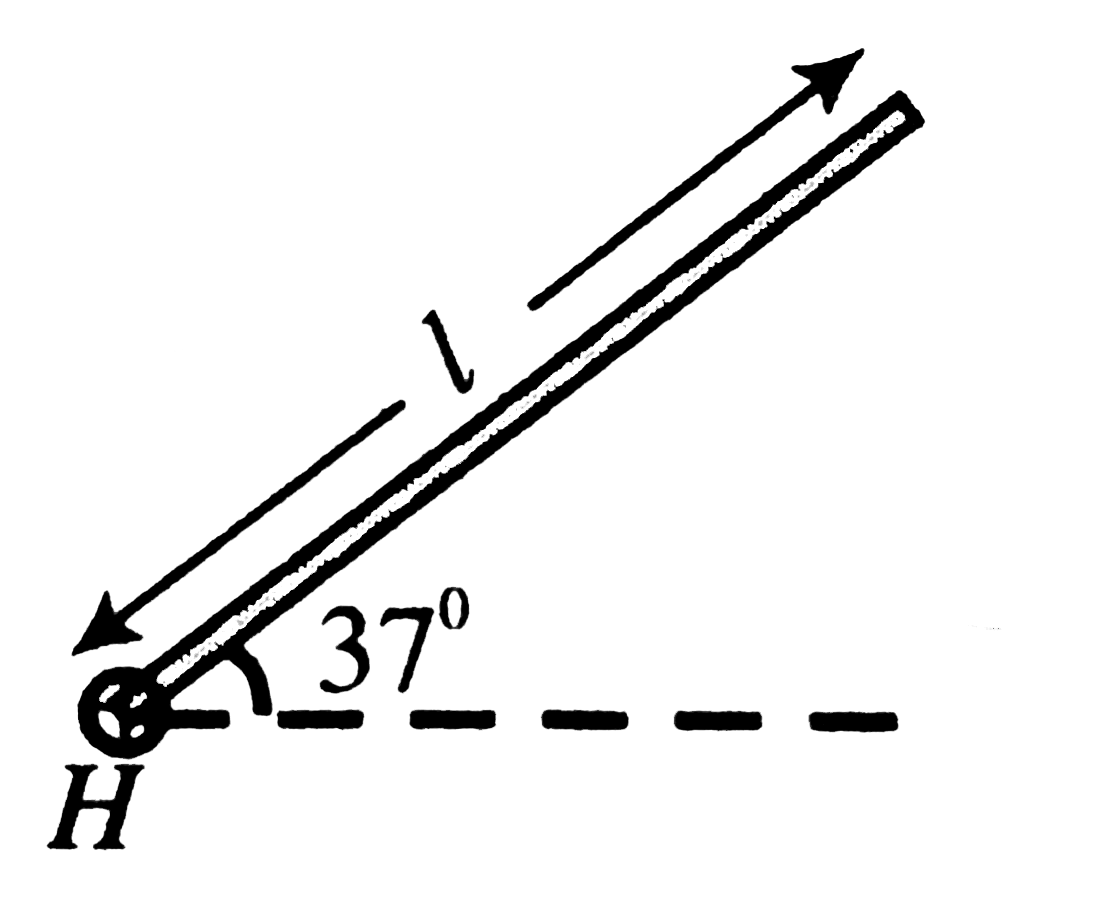
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A ring of mass m and radius r has a particle of mass m attached to it at a point A. the ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring is released from rest when AB is horizontal. find the angular velocity and the angular acceleration of the body when AB has turned through an angle π3.
View SolutionA uniform rod AB of mass 3m and length 4l, which is free to turn in a vertical plane about a smooth horizontal axis through A, is released from rest when horizontal. When the rod first becomes vertical, a point C of the rod, where AC=3l strikes a fixed peg. Find the linear impulse exerted by the peg on the rod if
(a). The rod is brought to rest by the peg.
(b). The rod rebounds and next comes to instantaneous rest inclined to the downward vertical at an angle π3 radian.
View SolutionA right triangular plate ABC of mass m is free to rotate in the verticle plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is
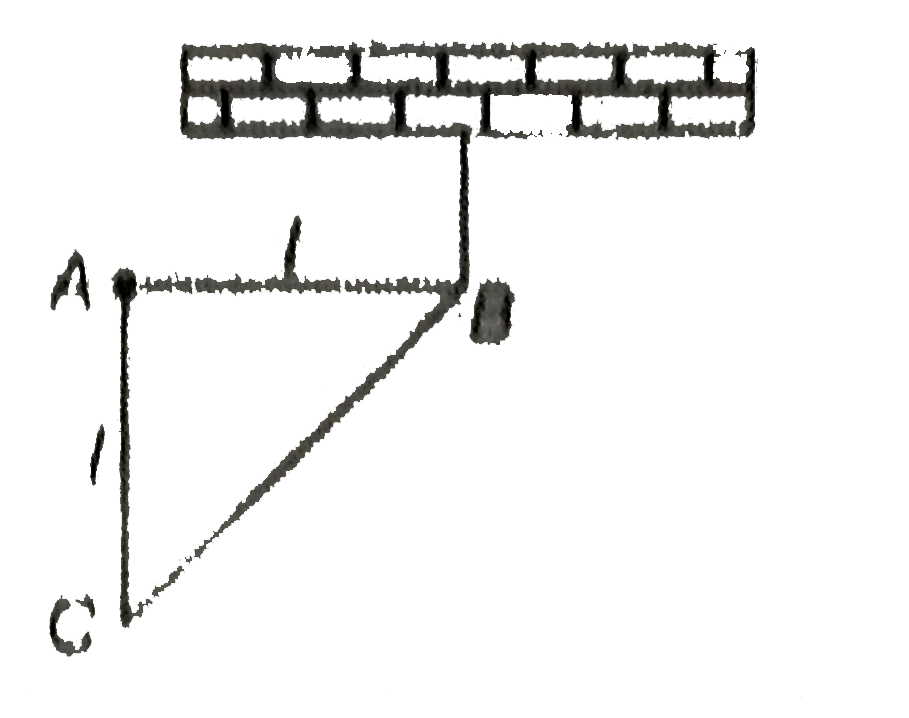
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
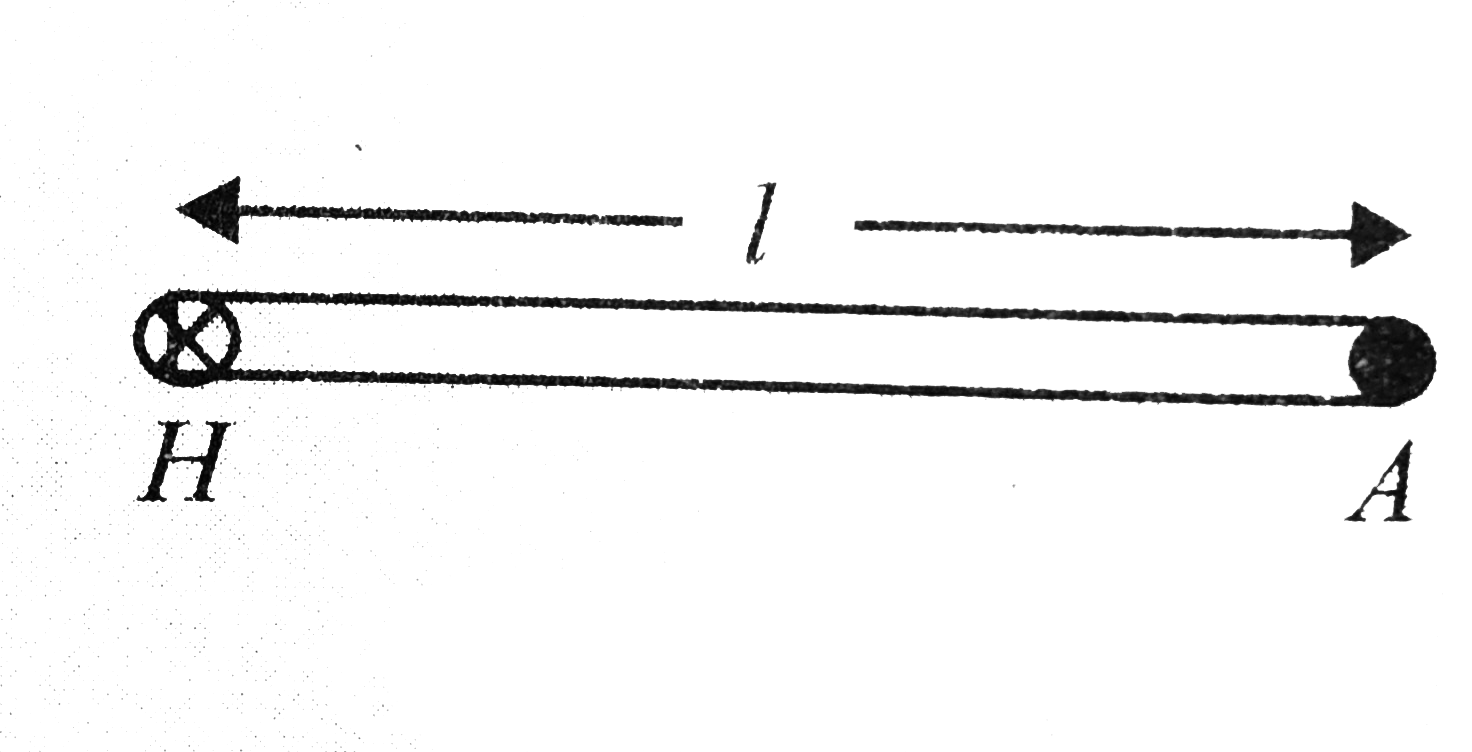
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution
