The moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
ML212
ML29
7ML248
ML248
The correct Answer is:B
To find the moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L3 from one of its ends and perpendicular to the rod, we can follow these steps:
Step 1: Identify the distances
We need to find the distance from the center of mass of the rod to the point where the axis is located. The center of mass of a uniform thin rod is located at its midpoint, which is at a distance of L2 from either end.
Given that the axis is at a distance of L3 from one end, we can calculate the distance from the center of mass to this point.
Distance from center of mass to point=L2−L3
Step 2: Calculate the distance
To perform the subtraction, we need a common denominator:
L2=3L6,L3=2L6
Now, subtract:
Distance=3L6−2L6=L6
Step 3: Use the parallel axis theorem
The parallel axis theorem states:
I=Icm+Md2
Where:
- I is the moment of inertia about the new axis,
- Icm is the moment of inertia about the center of mass,
- M is the mass of the rod,
- d is the distance from the center of mass to the new axis.
For a thin rod about its center of mass:
Icm=ML212
Now, substituting into the parallel axis theorem:
I=ML212+M(L6)2
Step 4: Calculate Md2
Calculating Md2:
Md2=M(L6)2=M⋅L236=ML236
Step 5: Combine the terms
Now, substituting back into the equation for I:
I=ML212+ML236
To combine these fractions, we need a common denominator, which is 36:
ML212=3ML236
Now, adding the two fractions:
I=3ML236+ML236=4ML236=ML29
Conclusion
Thus, the moment of inertia of the rod about the specified axis is:
ML29
We need to find the distance from the center of mass of the rod to the point where the axis is located. The center of mass of a uniform thin rod is located at its midpoint, which is at a distance of L2 from either end.
To perform the subtraction, we need a common denominator:
The parallel axis theorem states:
- I is the moment of inertia about the new axis,
- Icm is the moment of inertia about the center of mass,
- M is the mass of the rod,
- d is the distance from the center of mass to the new axis.
Calculating Md2:
Now, substituting back into the equation for I:
Thus, the moment of inertia of the rod about the specified axis is:
Similar Questions
The moment of inertia of a thing uniform rod of length L and mass M, about axis CD (as shown in figure) is

View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is
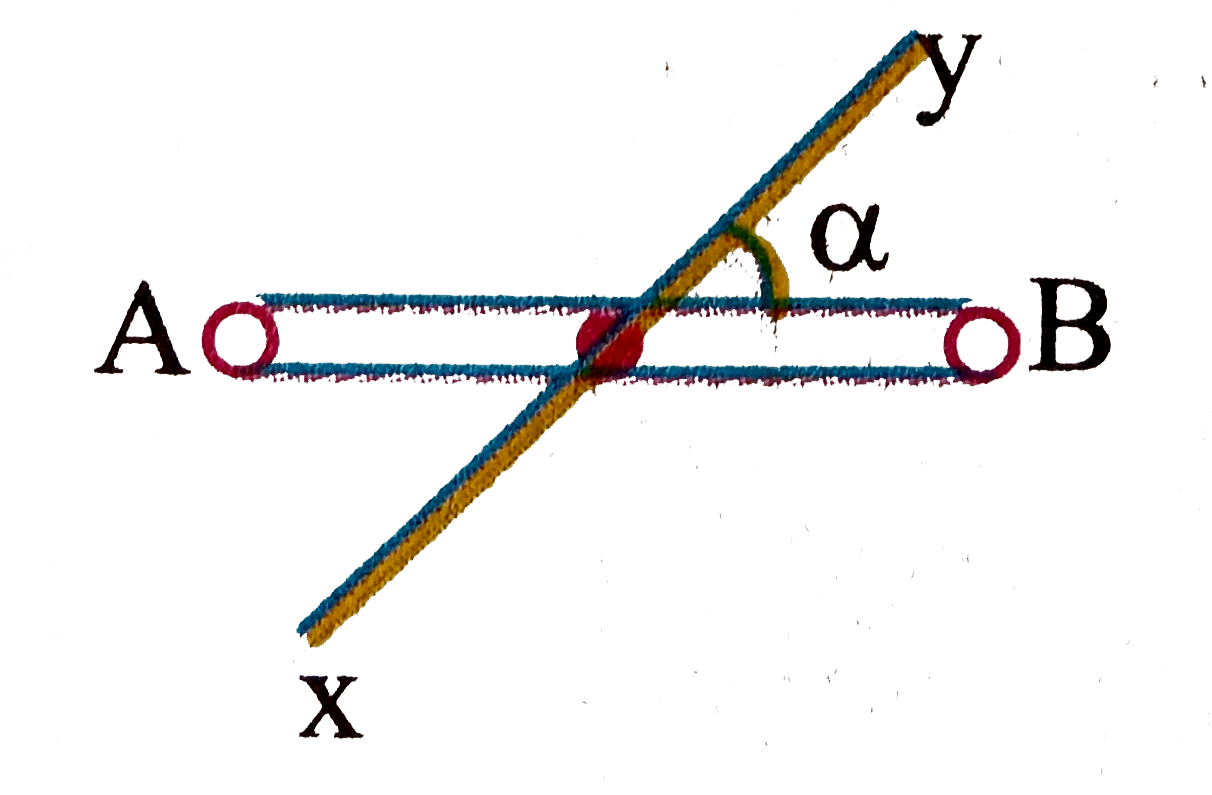
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionThe moment of inertia of a system of four rods each of length l and mass m about the axis shown is
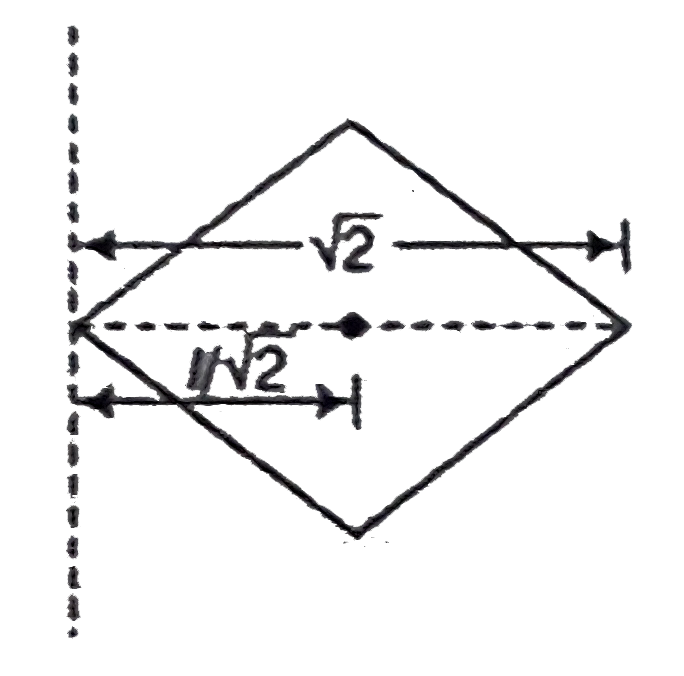
View SolutionThe radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionThe radius of gyration of a uniform rod of length l , about an axis passing through a point l8away form the centre of the rod , and perpendicular to it is:
View Solution

