In the given figure, two elastic rods P and Q are rigidly joined to end supports. A small mass m is moving with velocity v between the rods. All collisions are assumed to be elastic and the surface is given to be smooth. The time period of small mass m will be (A=area of cross section, Y=Young's modulus, L=length of each rod)
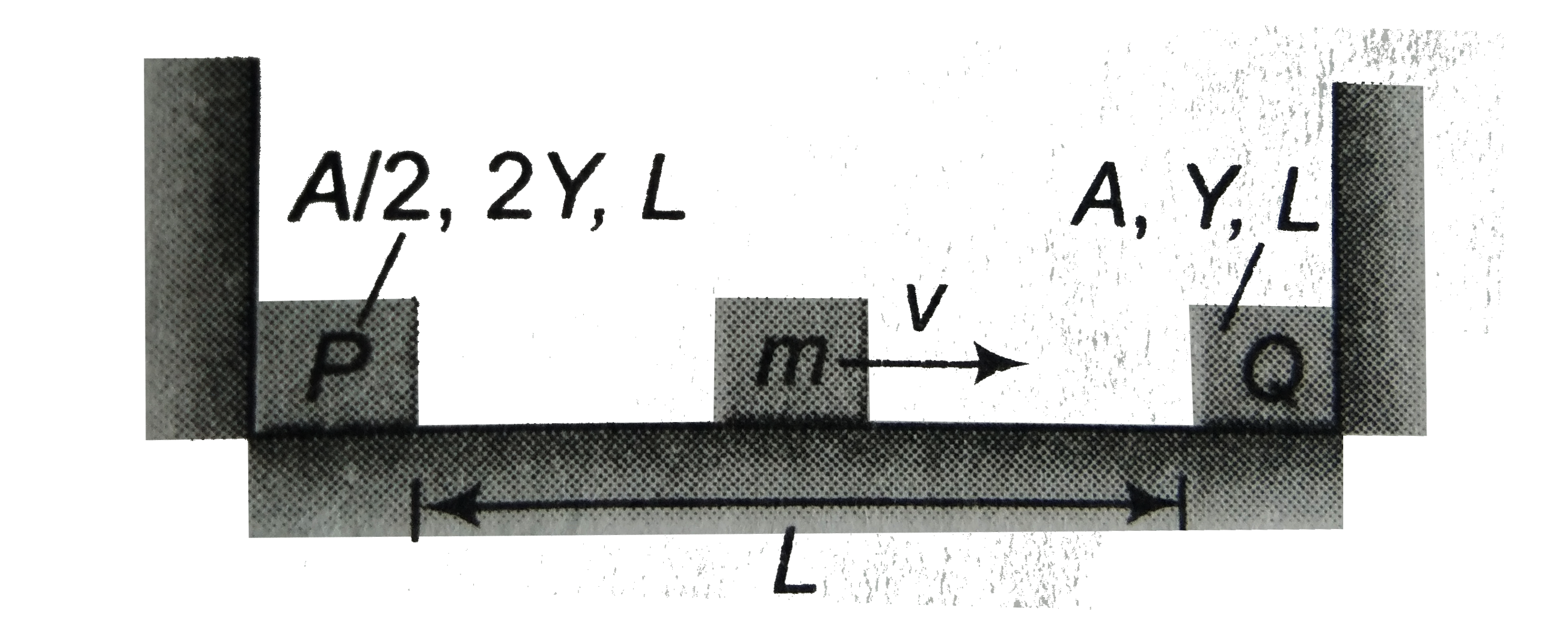
2Lv+2π√mLAY
2Lv+2π√2mLAY
2Lv+π√mLAY
2Lv
The correct Answer is:A
KQ=YAL
Kp=(2Y)(A/2)L=YAL
∴Kp=KQ=K=YAL
Half oscillation is completed with P and half with Q. But their value of K is same. Hence, we can say that in one oscillation one time period is comleted with spring.
T=(2Lv)+2π√mK=2Lv+2π√mLAY
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 More Than One Correct
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Comprehension
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is

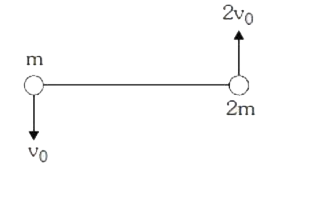
View SolutionTwo point masses of mass m and 2m placed on smooth horizontal plane are connected by a light rod of length l. Masses are given velocities in horizontal plane perpendicular to rod as shown. If area of cross section of rod is A and Young's modulus is Y, then elongation in the rod, will be
View Solution
Knowledge Check
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lgA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
A3√2V7LB√2V7LC√2V3LD3V7L
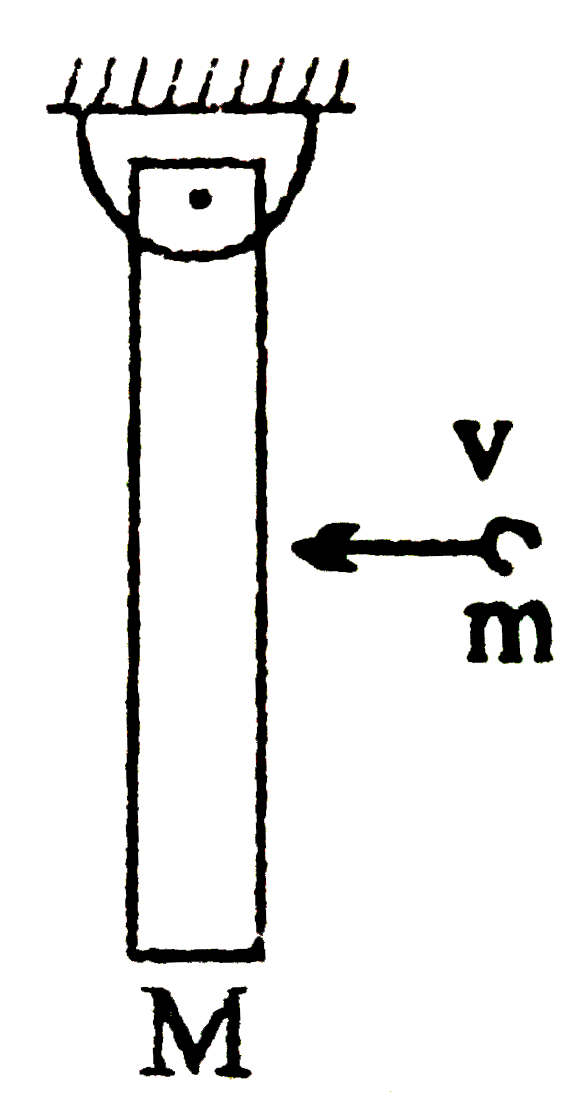
A uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

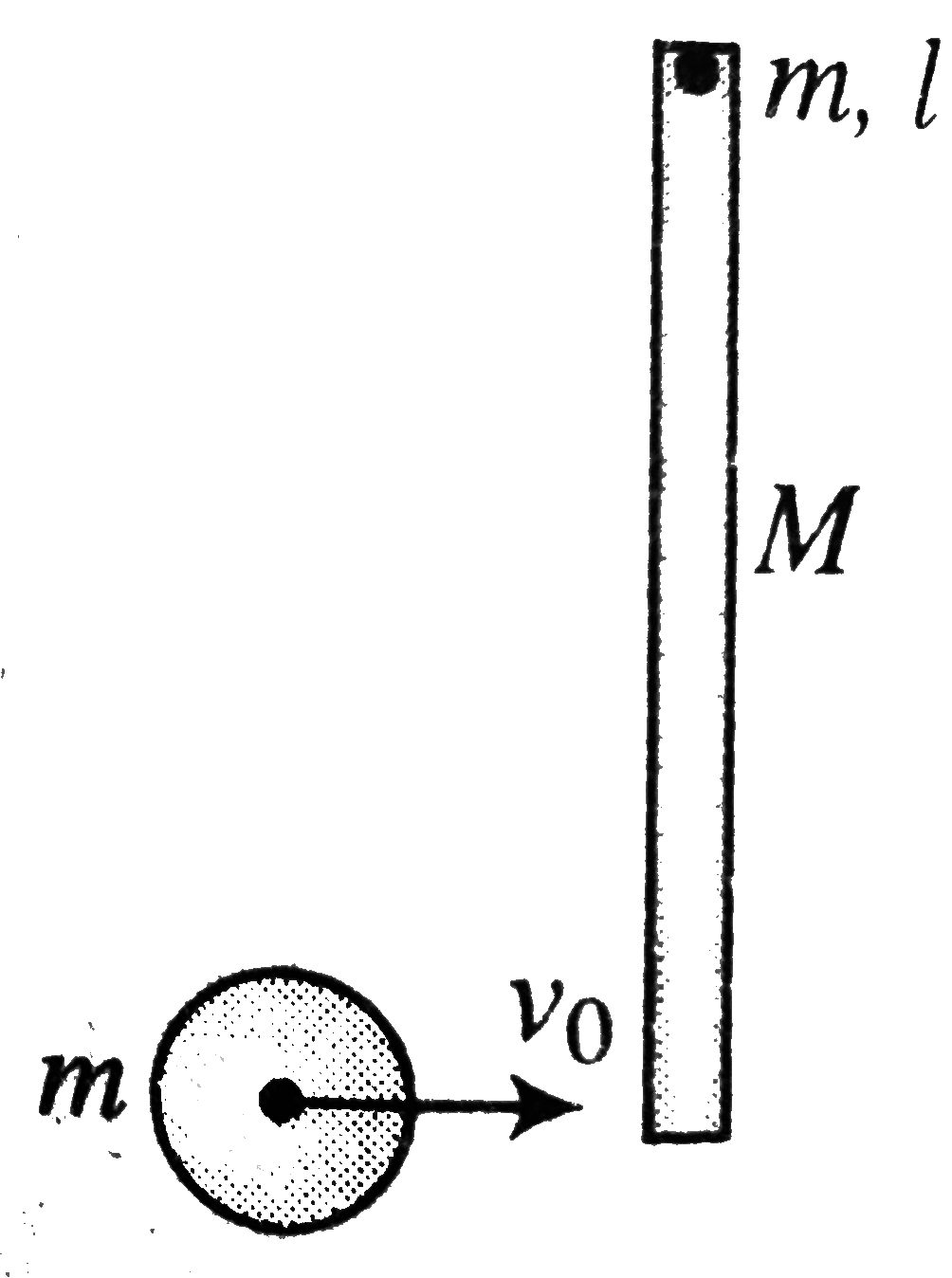
View SolutionA uniform rod of mass M is hinged at its upper end. A particle of mass m moving horizontally strikes the rod at its mid point elastically. If the particle comes to rest after collision find the value of M/m?
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View Solution

