A man of mass 60kg is standing on a platform executing SHM in the vertical plane. The displacement from the mean position varies as y=0.5sin(2πft). The value of f, for which the man will feel weightlessness at the highest point, is (y in metre)
g/4π
4πg
√2g2π
2π√2g
The correct Answer is:C
To solve the problem step by step, we need to analyze the conditions under which the man feels weightless at the highest point of the simple harmonic motion (SHM) on the platform.
Step 1: Understanding Weightlessness in SHM
Weightlessness occurs when the net force acting on the man is zero. At the highest point in SHM, the only forces acting on him are his weight (downward) and the centripetal force required for the circular motion (upward). For him to feel weightless, these forces must balance out.
Step 2: Setting Up the Equations
The condition for weightlessness can be expressed mathematically as:
m⋅a=m⋅g
Where:
- m is the mass of the man (60 kg),
- a is the maximum acceleration of the platform,
- g is the acceleration due to gravity (approximately 9.81m/s2).
At the highest point, the maximum acceleration a can be expressed in terms of the angular frequency ω and the amplitude A of the SHM:
amax=ω2⋅A
Step 3: Relating Angular Frequency to Frequency
The angular frequency ω is related to the frequency f by the equation:
ω=2πf
Thus, we can rewrite the maximum acceleration as:
amax=(2πf)2⋅A
Step 4: Substituting Values
Given that the amplitude A=0.5m, we can substitute this into the equation:
amax=(2πf)2⋅0.5
Step 5: Setting the Condition for Weightlessness
For the man to feel weightless:
(2πf)2⋅0.5=g
Substituting g≈9.81m/s2:
(2πf)2⋅0.5=9.81
Step 6: Solving for Frequency f
Rearranging the equation gives:
(2πf)2=9.810.5
(2πf)2=19.62
Taking the square root of both sides:
2πf=√19.62
f=√19.622π
Step 7: Calculating the Value of f
Calculating √19.62:
√19.62≈4.43
Now substituting back:
f≈4.432π
f≈4.436.2832
f≈0.706Hz
Final Answer
The value of f for which the man will feel weightlessness at the highest point is approximately:
f≈0.706Hz
---
Weightlessness occurs when the net force acting on the man is zero. At the highest point in SHM, the only forces acting on him are his weight (downward) and the centripetal force required for the circular motion (upward). For him to feel weightless, these forces must balance out.
The condition for weightlessness can be expressed mathematically as:
m⋅a=m⋅g
Where:
- m is the mass of the man (60 kg),
- a is the maximum acceleration of the platform,
- g is the acceleration due to gravity (approximately 9.81m/s2).
amax=ω2⋅A
The angular frequency ω is related to the frequency f by the equation:
ω=2πf
Thus, we can rewrite the maximum acceleration as:
amax=(2πf)2⋅A
Given that the amplitude A=0.5m, we can substitute this into the equation:
amax=(2πf)2⋅0.5
For the man to feel weightless:
(2πf)2⋅0.5=g
Substituting g≈9.81m/s2:
(2πf)2⋅0.5=9.81
Rearranging the equation gives:
(2πf)2=9.810.5
(2πf)2=19.62
Taking the square root of both sides:
2πf=√19.62
f=√19.622π
Calculating √19.62:
√19.62≈4.43
Now substituting back:
f≈4.432π
f≈4.436.2832
f≈0.706Hz
The value of f for which the man will feel weightlessness at the highest point is approximately:
f≈0.706Hz
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A horizontal platform with a mass of 100kg rotates at 10(r±) around a vertical axis passing through its centre. A man of mass 60kg is standing on its edge. The platform begins to rotaté with an angular velocity ω(r±), if the man "moves from the edge of the platform to its centre. Regard the platform as a circular homogeneous disk and the man as a point mass. Find the value of 3ω11.
View SolutionA body of mass 0.1 kg performing linear SHM experiences a restoring force of 1 N when its displacement from the mean position is 5 cm. Find (i) the force constant (ii) the period of SHM (iii) the acceleration of the body, when its displacement from the mean position is 1 cm./
View Solution
Knowledge Check
The equation for the displacement of a particle executing SHM is x=5sin(2πt)cm Then the velocity at 3cm from the mean position is( in cm//s)
A2πB3πC4πD8πThe displacement of a particle from its mean position (in metre) is given by
y=0.2sin(10πt+1.5π)cos(10πt+1.5π)
The motion of the particle isAperiodic but not simple harmonic motionBnon-periodicCsimple harmonic motion with period of 0.1 sDsimple harmonic motion with period of 0.2 sThe displacement of a particle from its mean position (in mean is given by y=0.2sin(10πt+1.5π)cos(10πt+1.5π). The motion but not S.H.M.
APeriodic but not S.H.MBNone-periodicCSimple harmonic motion with period 0.1sDSimple harmonic motion with period 0.2s
A man of mass 50 kg is standing on one end of a stationary wooden plank resting on a frictionless surface. The mass of the plank is 100 kg its length is 75 m and the coefficient of friction between the man the plank is 0.2 Find the least possible time (in sec) in which the man reach the other end starting from rest and stopping at the other end.
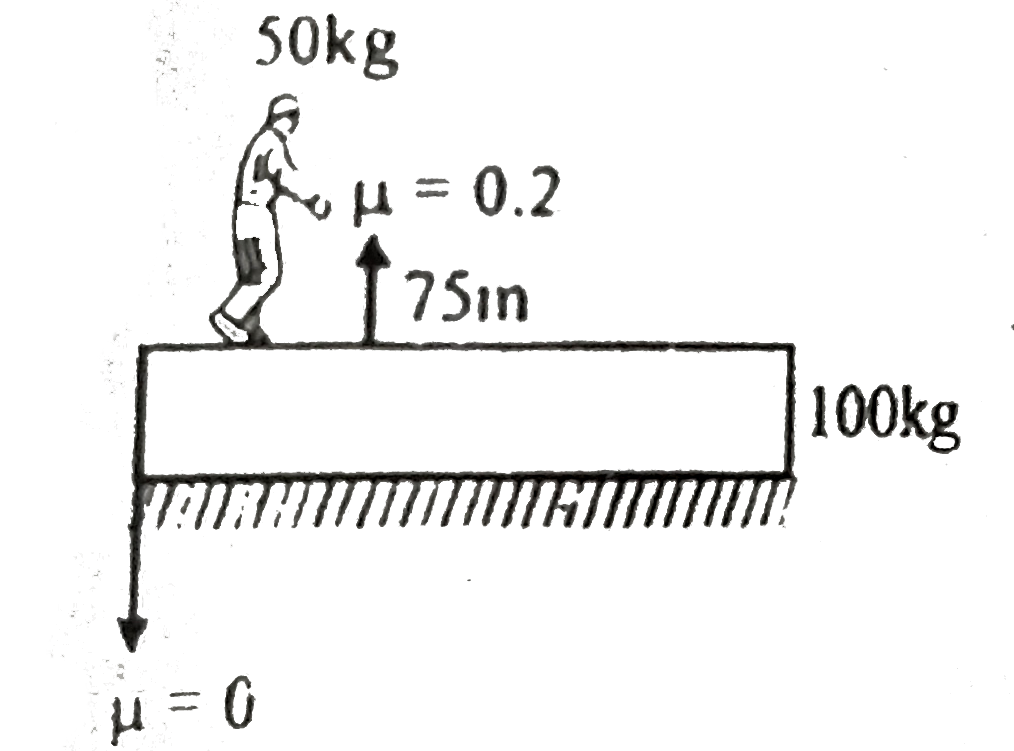
View SolutionA man of 80 kg mass is standing on the rim of a circular platform rotating about its axis. The platform with the man on it rotates at 12.0 r.p.m. How will the system rotate, if the man moves to the platform's centre? What work will the man perform in changing his position? The mass of the platform is 200 kg and its radius is 1.2 m.
View SolutionThe equation for the displacement of a particle executing SHM is y=5sin(2πt)cm. Find
(i) velocity at 3cm from the mean position
(ii) acceleration at 0.5s after having the mean position
View SolutionThe displacement of a particle from its mean position (in metre) is given by
y=0.2sin(10πt+1.5π)cos(10πt+0.5π).
The motion of particle is
View SolutionA man of mass 60 kg is standing on a boat of mass 140 kg, which is at rest in still water. The man is initially at 20 m from the shore. He starts walking on the boat for 4 s with constant speed 1.5 m/s towards the shore. The final distance of the man from the shore is
View Solution
