Part of SHM is graphed in the figure. Here, y is displacement from mean position. The correct equation describing the SHM is
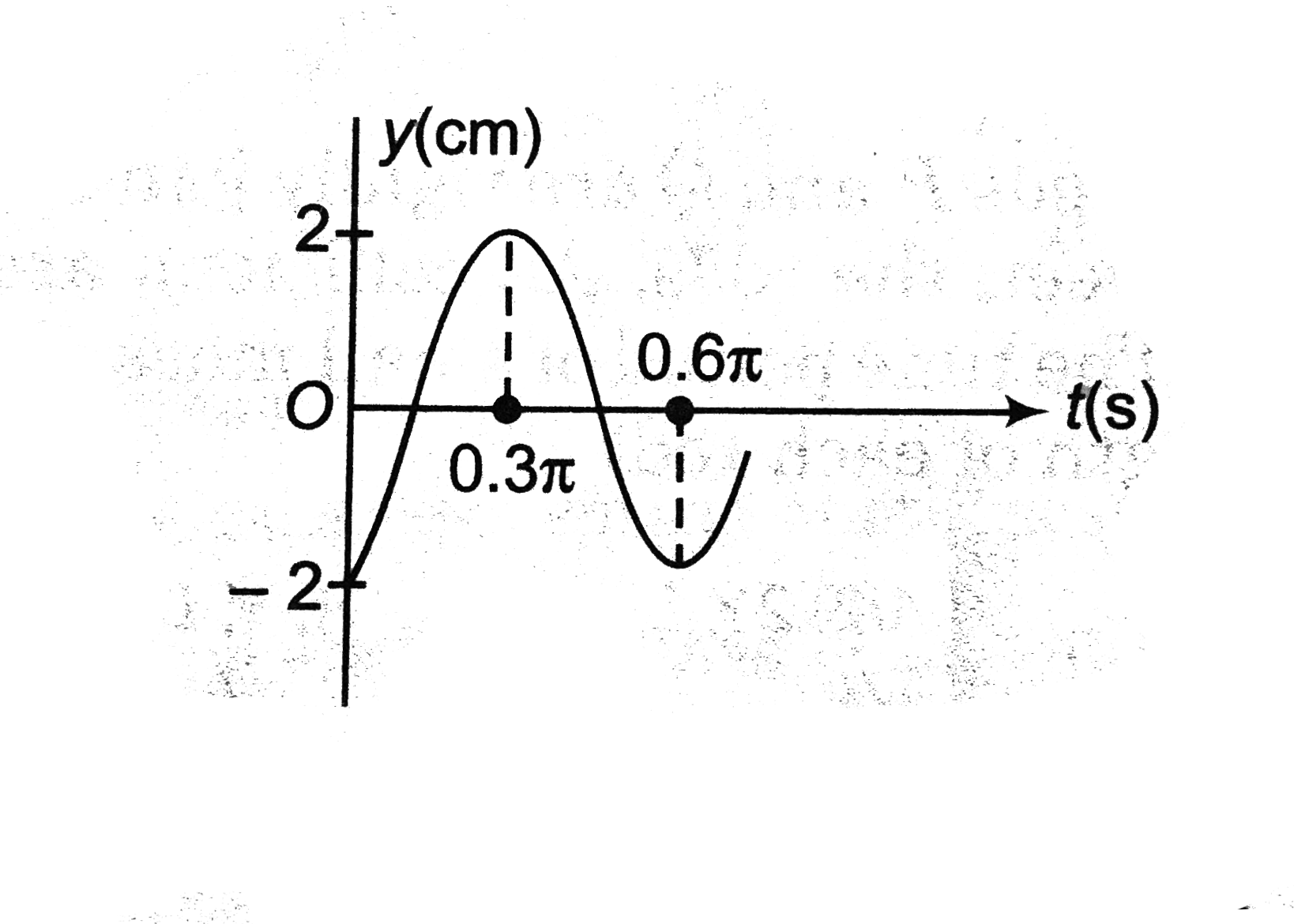
y=4cos(0.6t)
y=2sin(103t−π2)
y=2sin(π2−103t)
y=2cos(0.6t+π2)
The correct Answer is:B
T=0.6π
∴ω=2πT=2π0.6π
=103rad/s
Particle starts from y=−A=−2cm
∴y=−Acosωt
=Asin(ωt−π/2)
=2sin(103t−π/2).
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 More Than One Correct
Explore 8 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 2 Comprehension
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Level 1 Subjective
Explore 39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
If A is amplitude of a particle in SHM, its displacement from the mean position when its kinetic energy is thrice that to its potential energy
View SolutionThe potential energy of a particle of mass 2 kg in SHM is (9x2)J. Here x is the displacement from mean position . If total mechanical energy of the particle is 36 J. The maximum speed of the particle is
View Solution
Knowledge Check
Part of a simple harmonic motion is graphed in the figure, where y is the displacement from the mean position. The correct equation describing this S.H.M is-
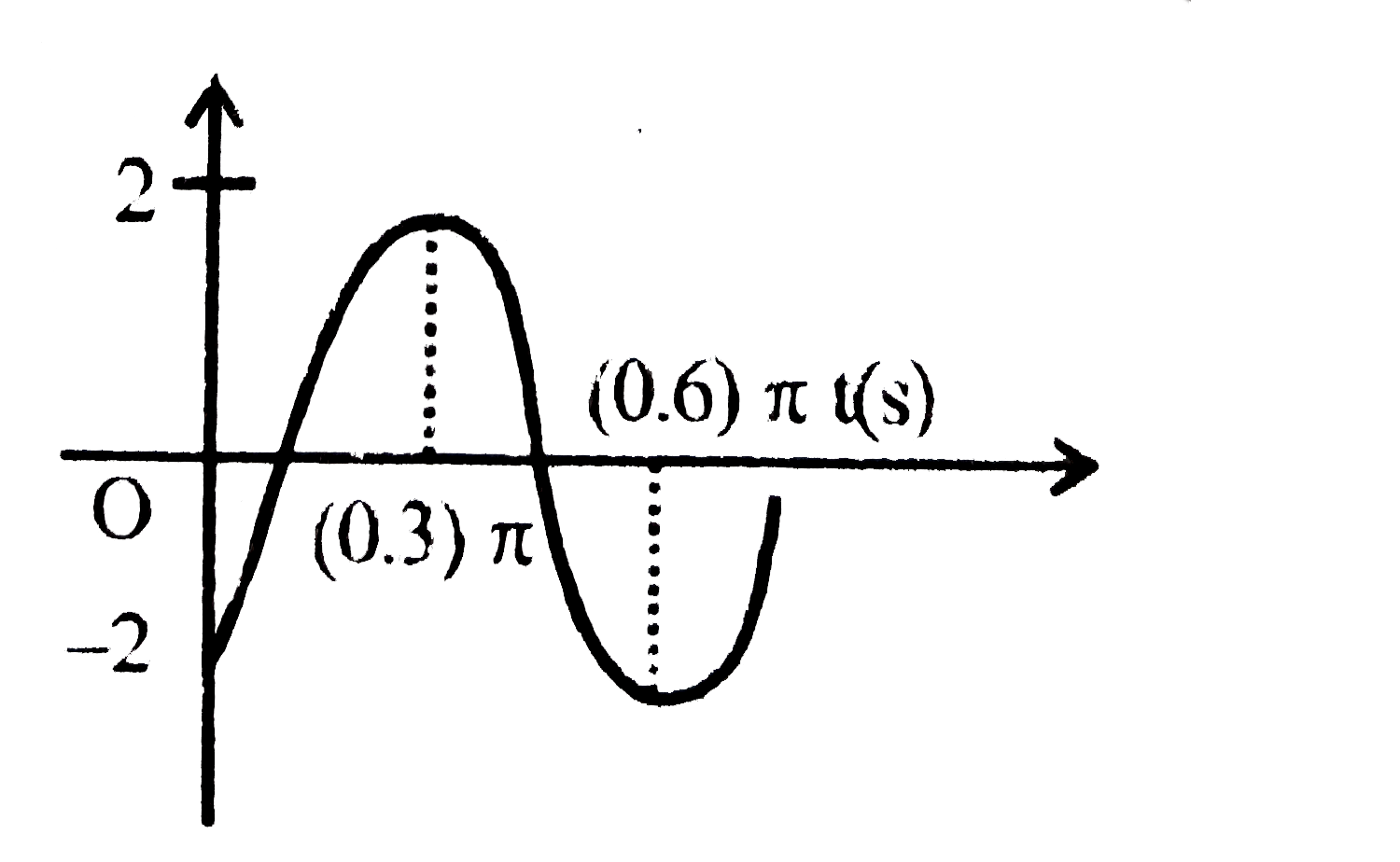 Ay=4cos(0.6t)By=2sin(103t−π2)Cy=4sin(103t+π2)Dy=2cos(103t+π2)
Ay=4cos(0.6t)By=2sin(103t−π2)Cy=4sin(103t+π2)Dy=2cos(103t+π2)The velocity of a particle in simple harmonic motion at displacement y from mean position is
Aω√(a2+y2)Bω√(a2−y2)CwyDω2√(a2+y2)In SHM, acceleration versus displacement (from mean position) graph:
Ais always a straight line passing through origin and slope-1Bis always a stright line passing through origin and slope+1Cis always a stright line not necessarily passing through oringinDnone of the above
The figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
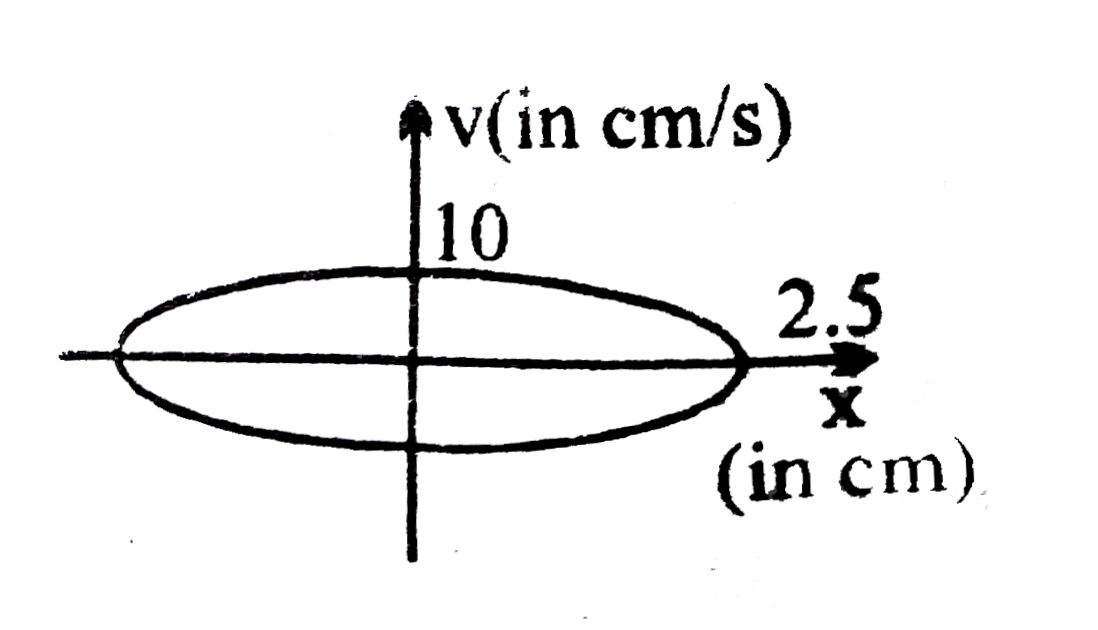
View SolutionA particle of mass 1kg is udnergoing S.H.M., for which graph between force and displacement (from mean position) as shown.
Its time period, in seconds, is-
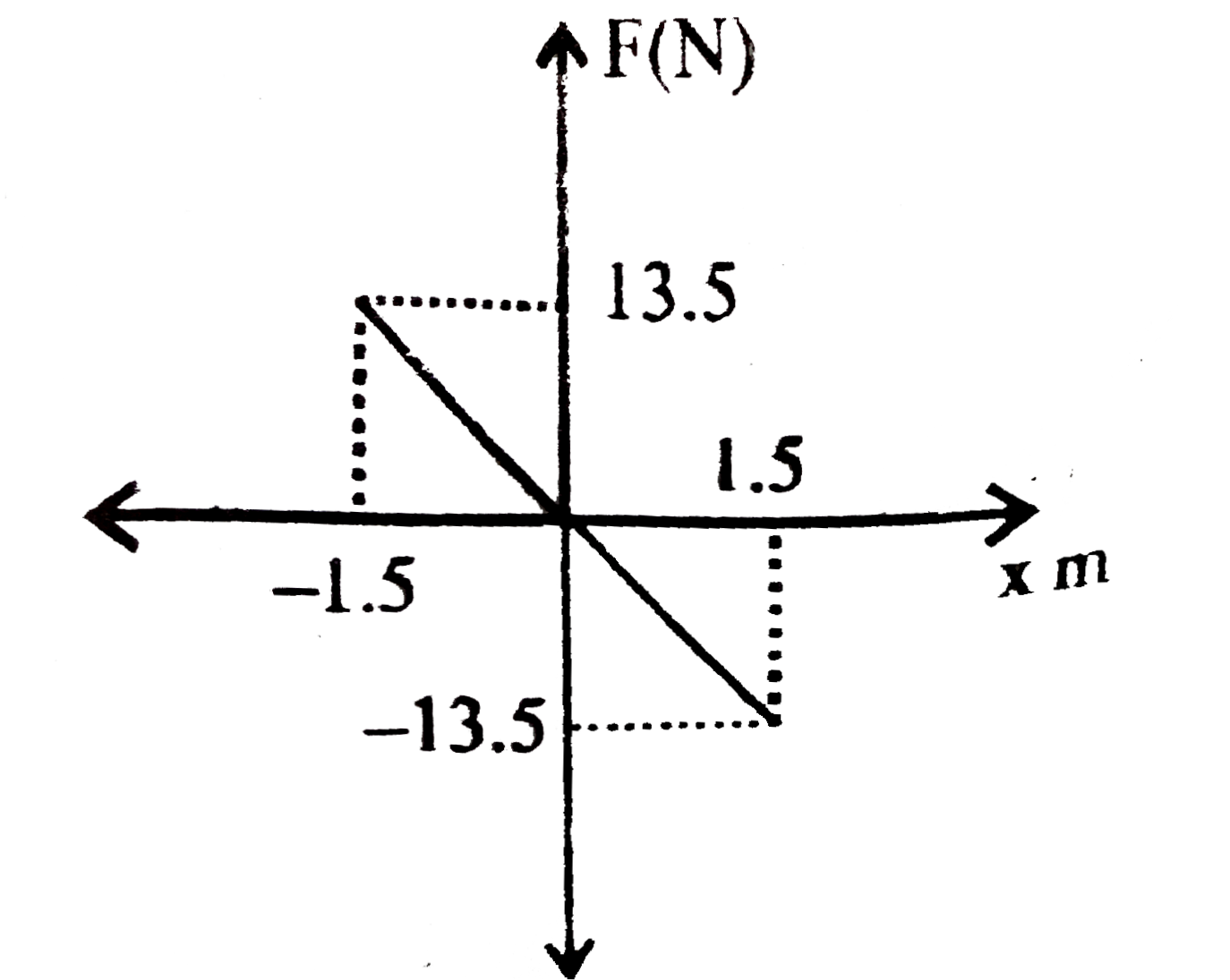
View SolutionThe amplitude of oscillation of particles in SHM is √3cm. The displacement from mean position at which its potential and kinetic energies are in the ratio 1:2 is
View SolutionA particle is performing SHM. if its displacement from mean position is x, a corresponding resultant force on y is F and acceleration is a, which of the following graph is correct?
View SolutionFigure shows the position -time graph of an object in SHM. The correct equation representing this motion is

View Solution

