A block of mass m, when attached to a uniform ideal apring with force constant k and free length L executes SHM. The spring is then cut in two pieces, one with free length n L and other with free length (1−n)L. The block is also divided in the same fraction. The smaller part of the block attached to longer part of the spring executes SHM with frequency f1 . The bigger part of the block attached to smaller part of the spring executes SHM with frequency f2. The ratio f1/f2 is
1
n1−n
1+nn
n1+n
The correct Answer is:A
To solve the problem, we need to find the ratio of the frequencies f1 and f2 of two blocks attached to different parts of a spring after it has been cut. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the Spring Constant
The spring constant k is inversely proportional to the length of the spring. If the original spring has a length L and spring constant k, then when the spring is cut into two parts:
- The longer part with length nL will have a spring constant:
k1=kn
- The shorter part with length (1−n)L will have a spring constant:
k2=k1−n
Step 2: Dividing the Mass
The mass m is also divided in the same ratio:
- The smaller part of the mass (attached to the longer spring) is:
m1=n⋅m
- The larger part of the mass (attached to the shorter spring) is:
m2=(1−n)⋅m
Step 3: Finding the Frequencies
The frequency of a mass-spring system executing simple harmonic motion (SHM) is given by:
f=12π√km
Using this formula, we can find the frequencies f1 and f2:
- For the smaller mass m1 attached to the longer spring:
f1=12π√k1m1=12π√knn⋅m=12π√kn2m
- For the larger mass m2 attached to the shorter spring:
f2=12π√k2m2=12π
⎷k1−n(1−n)⋅m=12π√k(1−n)2m
Step 4: Finding the Ratio of Frequencies
Now we can find the ratio f1f2:
f1f2=√kn2m√k(1−n)2m=√(1−n)2√n2=1−nn
Thus, the ratio of the frequencies is:
f1f2=1−nn
Final Answer
The ratio f1f2 is 1−nn.
---
The spring constant k is inversely proportional to the length of the spring. If the original spring has a length L and spring constant k, then when the spring is cut into two parts:
- The longer part with length nL will have a spring constant:
k1=kn
- The shorter part with length (1−n)L will have a spring constant:
k2=k1−n
The mass m is also divided in the same ratio:
- The smaller part of the mass (attached to the longer spring) is:
m1=n⋅m
- The larger part of the mass (attached to the shorter spring) is:
m2=(1−n)⋅m
The frequency of a mass-spring system executing simple harmonic motion (SHM) is given by:
f=12π√km
Using this formula, we can find the frequencies f1 and f2:
f1=12π√k1m1=12π√knn⋅m=12π√kn2m
f2=12π√k2m2=12π
⎷k1−n(1−n)⋅m=12π√k(1−n)2m
Now we can find the ratio f1f2:
f1f2=√kn2m√k(1−n)2m=√(1−n)2√n2=1−nn
f1f2=1−nn
The ratio f1f2 is 1−nn.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Knowledge Check
In a spring- mass system , the length of the spring is L, and it has a mass M attached to it and oscillates with an angular frequency ω. The spring is then cut into two parts, one (i) with relaxed length αL and the other (ii) with relaxed length (1−α) L. The force constants of the two spring A and B are
Ak1−α and kαBkα and k1−αCαk,(1−α)kDk and kA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
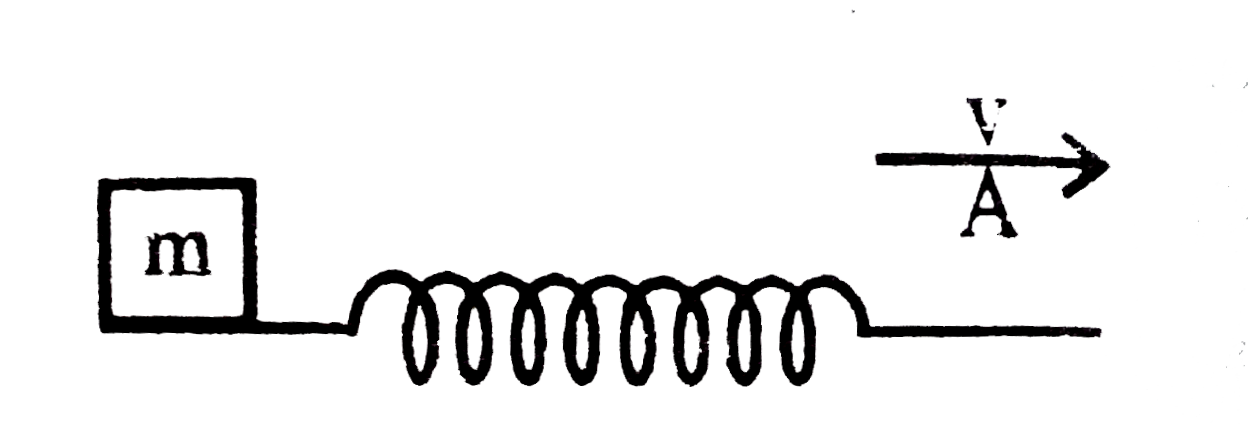 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
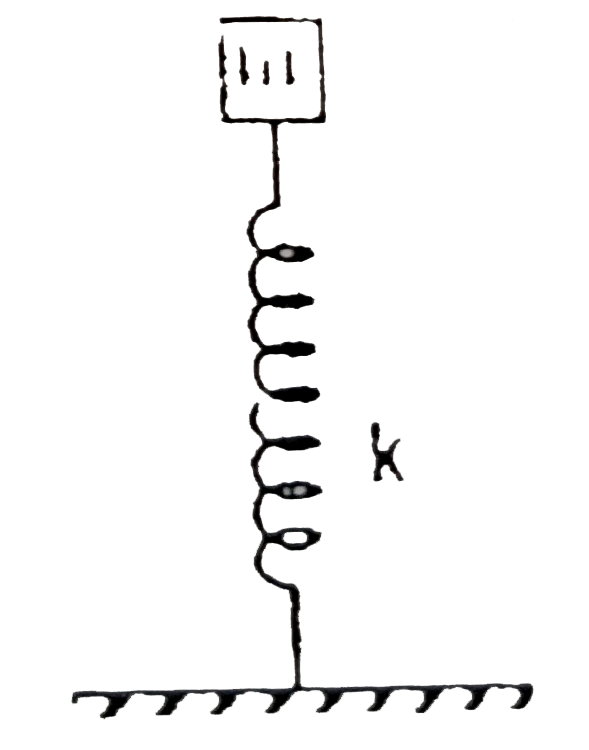 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπ
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
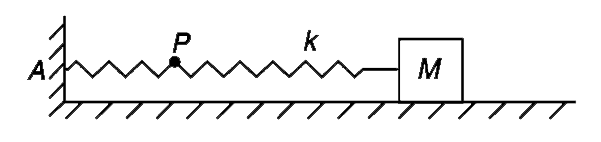
View SolutionA spring of force constant k is cut into two pieces whose lengths are in the ratio 1:2. The force constant of the longer piece?
View SolutionA spring of force constant K is attached with a mass executes with S.H.M has a time period T. It is cut into three equal parts
If the spring are attached to the load as shown in figure then effective spring constant is
View SolutionA spring of force constant K is attached with a mass executes with S.H.M has a time period T. It is cut into three equal parts
If the springs are connected in parallel then the time period of the combination for the same mass is
View Solution
