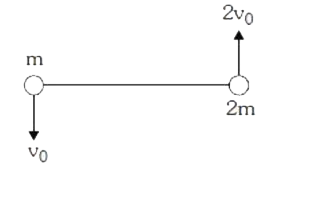
Two point masses of mass m and 2m placed on smooth horizontal plane are connected by a light rod of length l. Masses are given velocities in horizontal plane perpendicular to rod as shown. If area of cross section of rod is A and Young's modulus is Y, then elongation in the rod, will be
mv20AY
2mv20AY
6mv20AY
3mv20AY
The correct Answer is:C
T2m+Tm=(3v0)2l
T=6mv20l
Y=6mv20lΔl/Y⇒Δl=6mv20AY.
Topper's Solved these Questions
Similar Questions
A rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is

View SolutionA rod PQ of length L revolves in a horizontal plane about the axis YY´. The angular velocity of the rod is w. If A is the area of cross-section of the rod and r be its density, its rotational kinetic energy is
View Solution
Knowledge Check
A uniform rod of mass m and length l is rotating with constant angular velocity ω about an axis which passes thorugh its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young's modulus is y. Neglect gravity. The strain at the mid point of the rod is:
Amn2l8AyB3mω2l8AyC3mω2l4AyDmω4AyA rod of mass M and length l is placed on a smooth horizontal table and is hit by a ball moving horizontally and prependicular to length of rod and sticks to it Then conservation of angular momentum can be applied:
AAbout any point on the rodBAbout a point at the centre of the rodCAbout end point of the rodDNoneA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
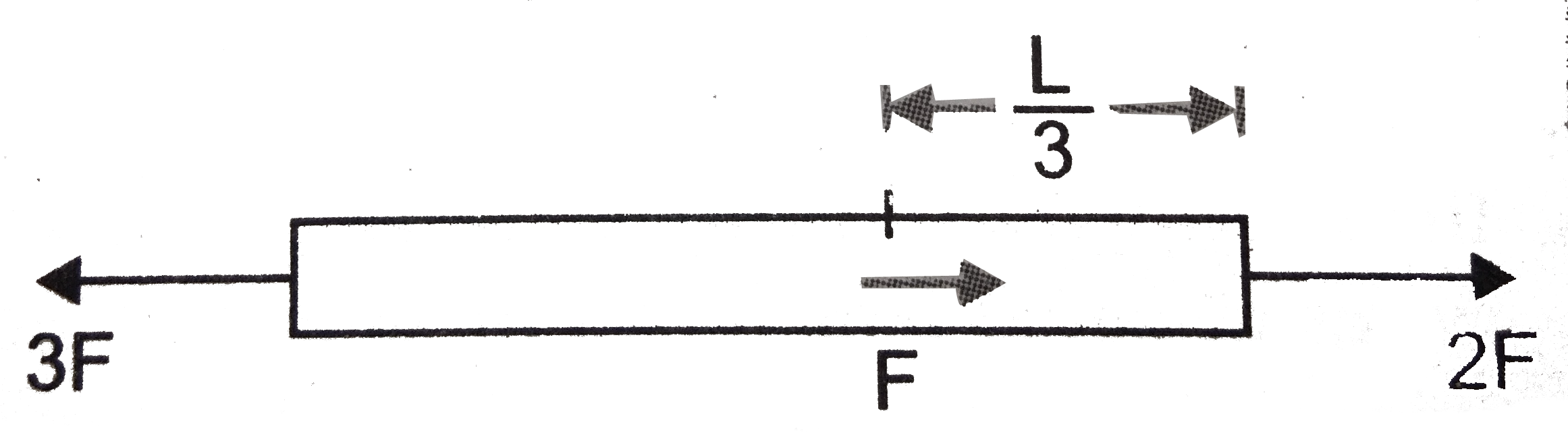 A2FL5AYB3FL5AYC3FL8AYD8FL3AY
A2FL5AYB3FL5AYC3FL8AYD8FL3AY
A rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View SolutionA uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View Solution

