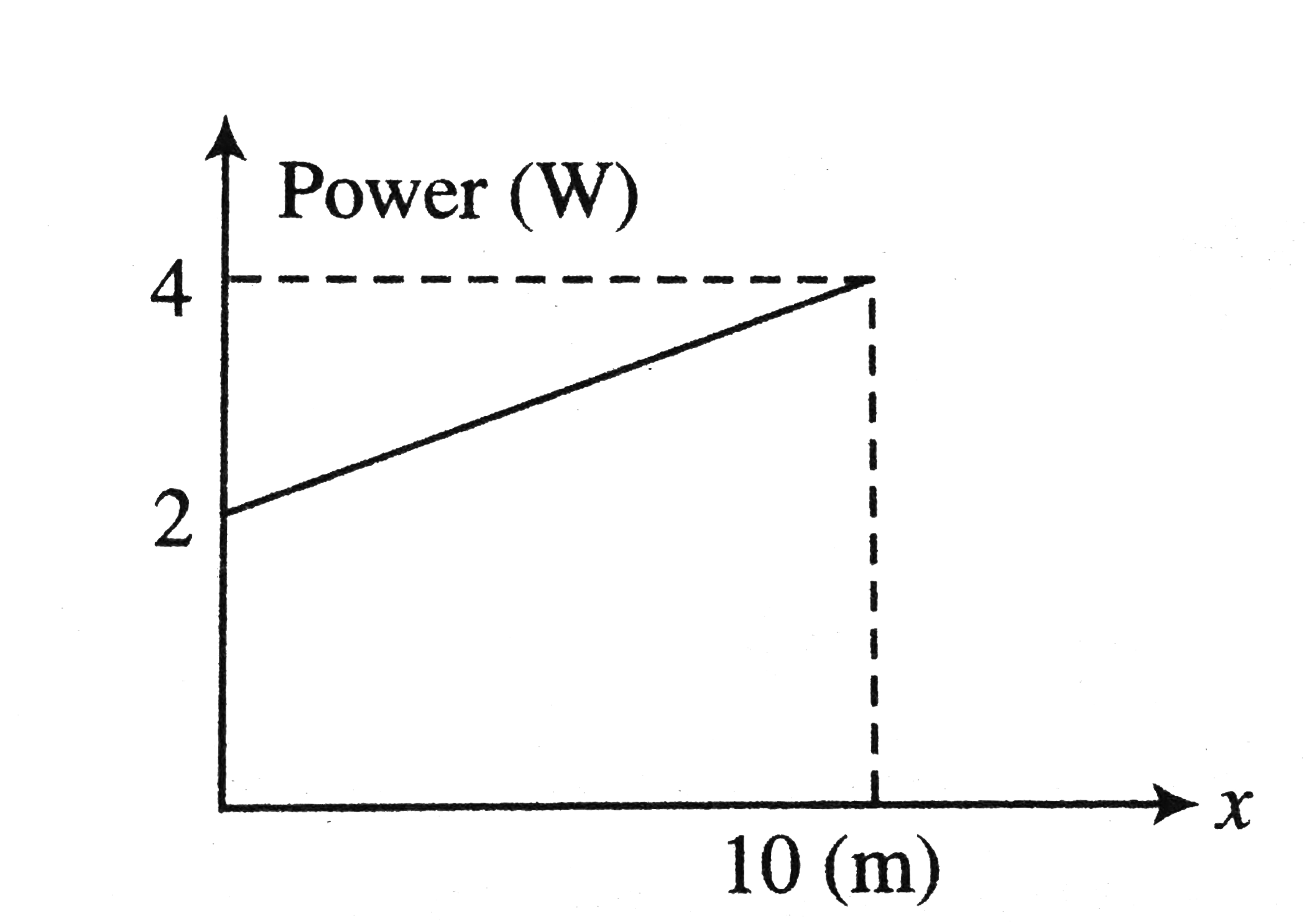
A particle A of mass $10 / 7 k g$ is moving in the positive direction of $x - a ξ s$ . At initial position $x = 0$ , its velocity is $1 m s^{- 1}$ , then its velocity at $x = 10 m$ is (use the graph given)

(a) $4 m s^{- 1}$

(b) $2 m s^{- 1}$

(d) $\frac{100}{3} m s^{- 1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

The velocity of a particle moving in the positive direction of x-axis veries as $v = 10 \sqrt{x}$ . Assuming that at $t = 0$ , particle was at $x = 0$
AThe initial velocity of the particle is zero
Bthe initial velocity of the particle is $2.5 \frac{m}{s}$ .
CThe accelration of the particle is $2.5 \frac{m}{s^{2}}$ .
DThe acceleration of the particle is $50 \frac{m}{s^{2}}$ .
A particle of mass $10^{31}$ kg is moving with a velocity equal to $10^{5} m s^{- 1}$ . The wavelength of the particle is equal to
A0
B $6.6 \times 10^{- 8} m$
C0.66m
D $1.5 \times 10^{7} m$
A particle moving in the positive x-direction has initial velocity $v_{0}$ . The particle undergoes retardation $k v^{2}$ , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
A $v = v_{0} / (1 + k v_{0} t)$
B $v = \frac{2 v_{0}}{1 + k t}$
C $v = \frac{v_{0}}{k t}$
D $v = \frac{v_{0}}{(1 + k^{2} v_{0}^{2} t)}$