A particle of mass m slides on a frictionaless surface ABCD, starting from rest as shown in figure. The part BCD is a circular arc. If it looses contact at point P, the maximum height attained by the particle from point C is

(a) R[2+12√2]
(b) R[1+12√2]R
(c) 3R
(d) None of these
The correct Answer is:A
Applying conservation of energy, we get
2mgR−mgR√2=12mu2⇒u=√4gR−√2gR

Hmax=R+R√2+u2sin245∘2g
=R+R√2+4gR−√2gR2g×2
=2R+R√2−R2√2R[2+12√2]
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A particle is thrown upward with speed 20√2 m/s. It strikes the inclined surface as shown in the figure. Collision of particle and inclined surface is perfectly inelastic. What will be maximum height (in m) attained by the particle from the ground (g=10ms2)
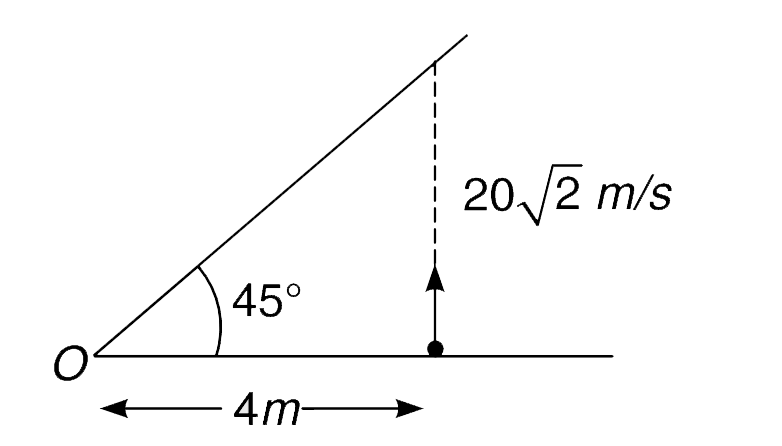
View SolutionA particle starting from rest undergoes a rectilinear motion with acceleration a. The variation of a with time t is shown below. The maximum velocity attained by the particle during its motion is
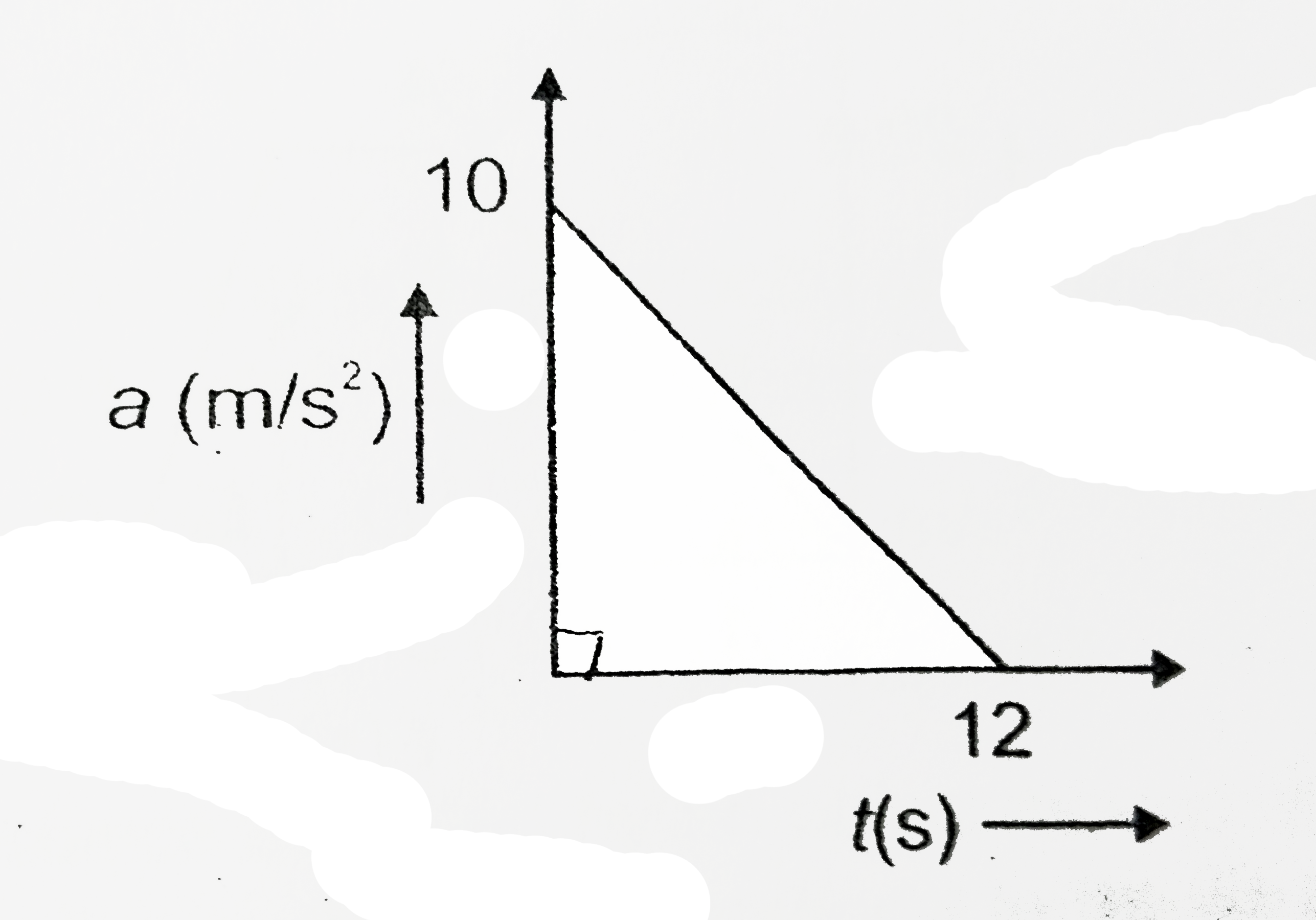
View Solution
Knowledge Check
A particle of mass m slides on a frictionaless surface ABCD, starting from rest as shown in figure. The part BCD is a circular arc. If it looses contact at point P, the maximum height attained by the particle from point C is
 AR(2+12√2)BR(2−12√2)C3 RD(1+12√2)R
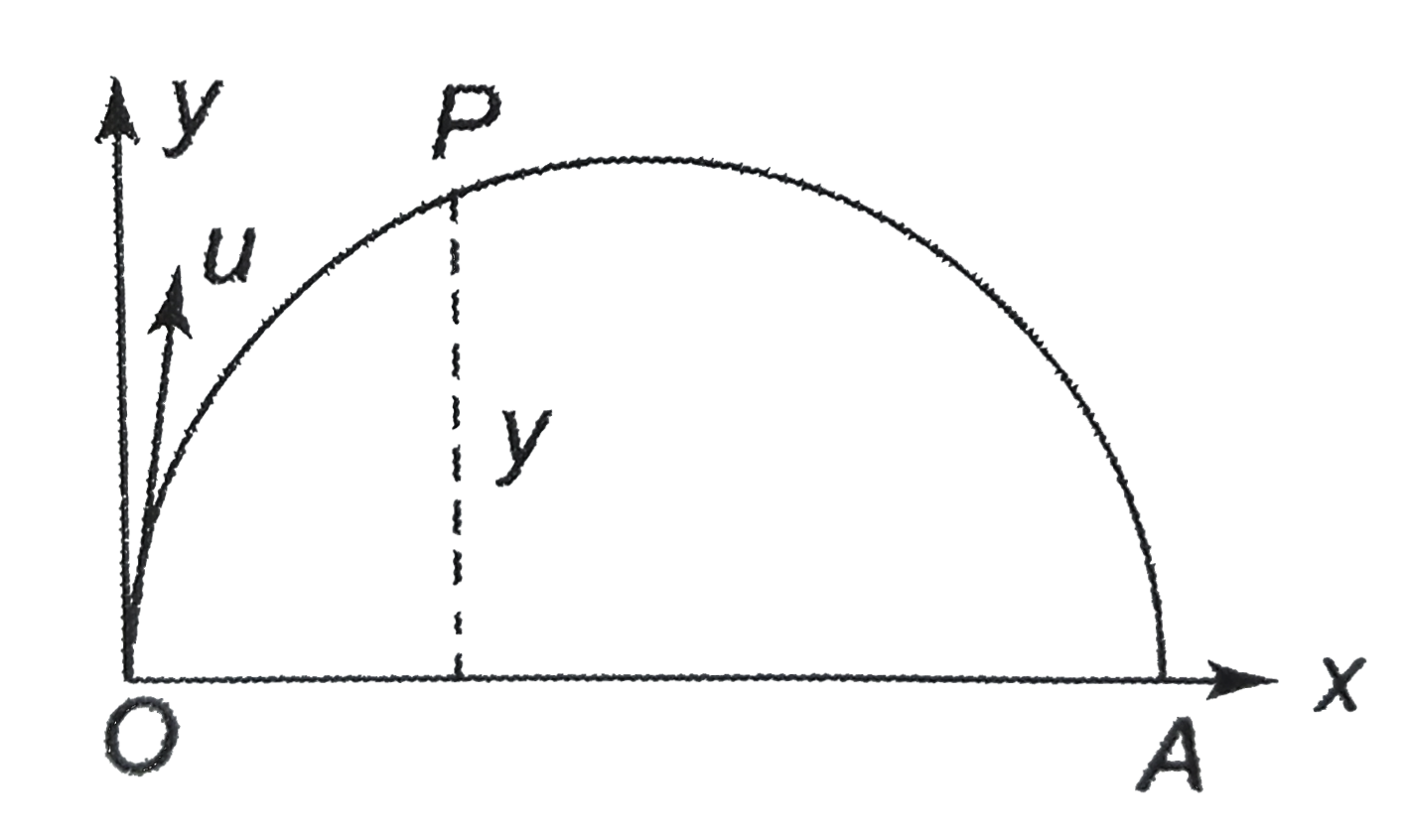
AR(2+12√2)BR(2−12√2)C3 RD(1+12√2)RA particle slides down a frictionless paraboli (y=x2) track (A−B−C) starting from rest at point A.Point B is at the vertex of parabola and point C is at a height less than that of point A.After C,the particle moves freely in air as a projectile. If the particle reaches highest point at P,then
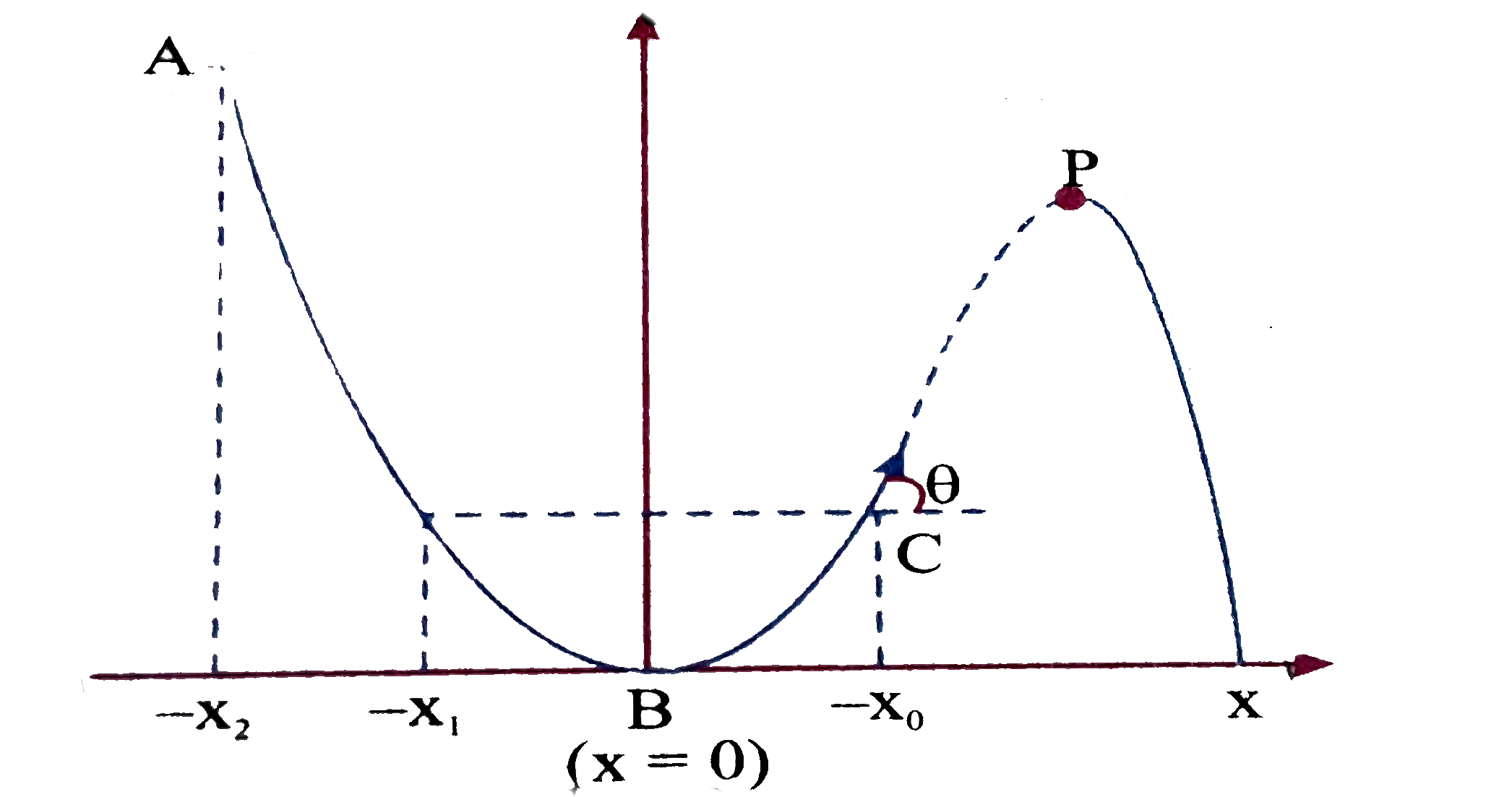 AKE at P=KE at BBheight at P=height at ACtotal energy at P=total energy at ADtime of travel from A to B =time of travel from B to P
AKE at P=KE at BBheight at P=height at ACtotal energy at P=total energy at ADtime of travel from A to B =time of travel from B to PA graph of acceleration versus time of a particle starting from rest at t=0 is as shown in figure. The speed of the particle at t=14s is
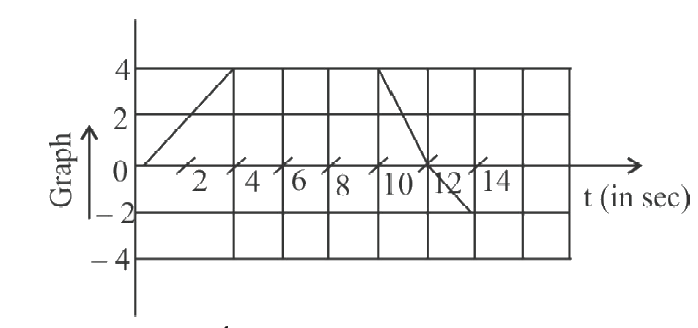 A2ms−1B34ms−1C20ms−1D42ms−1
A2ms−1B34ms−1C20ms−1D42ms−1
A particle is thrown at an angle with horizontal from the ground. After 4s it reaches to a point P and after 5 more seconds it strikes the ground. Find the height of P the maximum height attained by the particle.
View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant

View SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?

View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :-
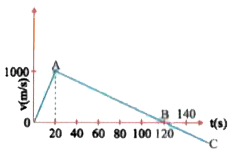
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :-

View Solution