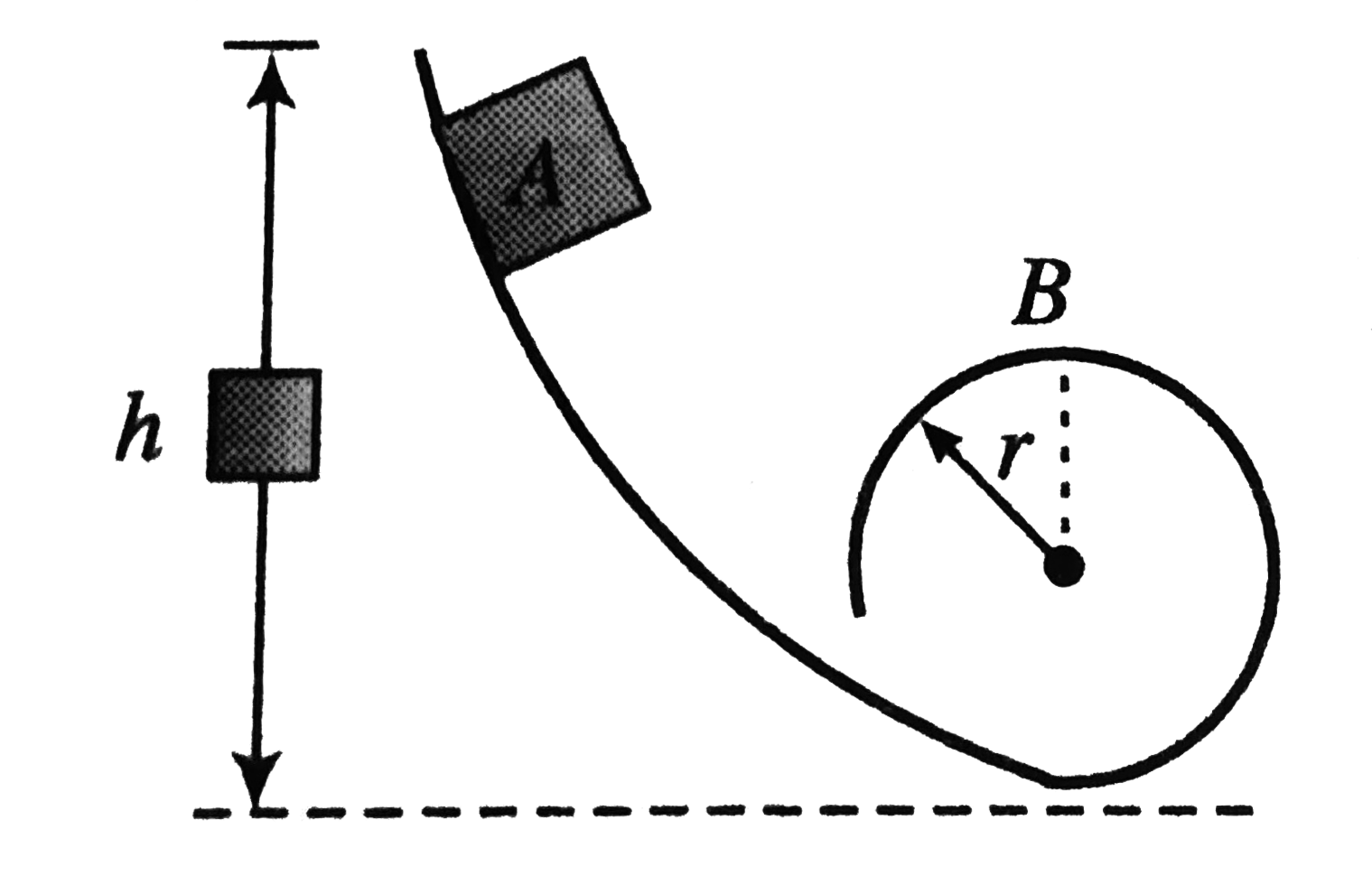
A mass m starting from A reaches B of a frictionless track. On reaching B, it pushes the track with a force equal to x times its weight, then the applicable relation is
(a) h=(x+5)2r
(b) h=x2r
(c) h=r
(d) h=(x+12)r
The correct Answer is:A
KE of blocks at B=PE at A−PE at B
12mv2=mgh−mg2r=mg(h−2r)
v2=2g(h−2r) (i)
Also, mv2r=xmg+mg
or v2=(x+1)rg (ii)
Equating Eqs (i) and (ii), we get 2g(h−2r)=(x+1)gr
or 2gh=(x+1)gr+4gr=(x+5)gr
h=(x+52)r
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
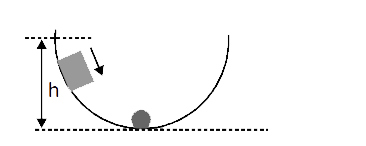
A block of mass m starts from rest and slides down a frictionless semi-circular track from a height h as shown. When it reaches the lowest point of the track, it collides with a stationary piece of putty also having mass m. If the block and the putty stick together and continue to slide, the maximum height that the block-putty system could reach is
View SolutionThe block on the loop shown slides without friction. At what height from A it starts so that it passes against the track at B with a net upward force equal to its own weight? The radius of the loop is R.
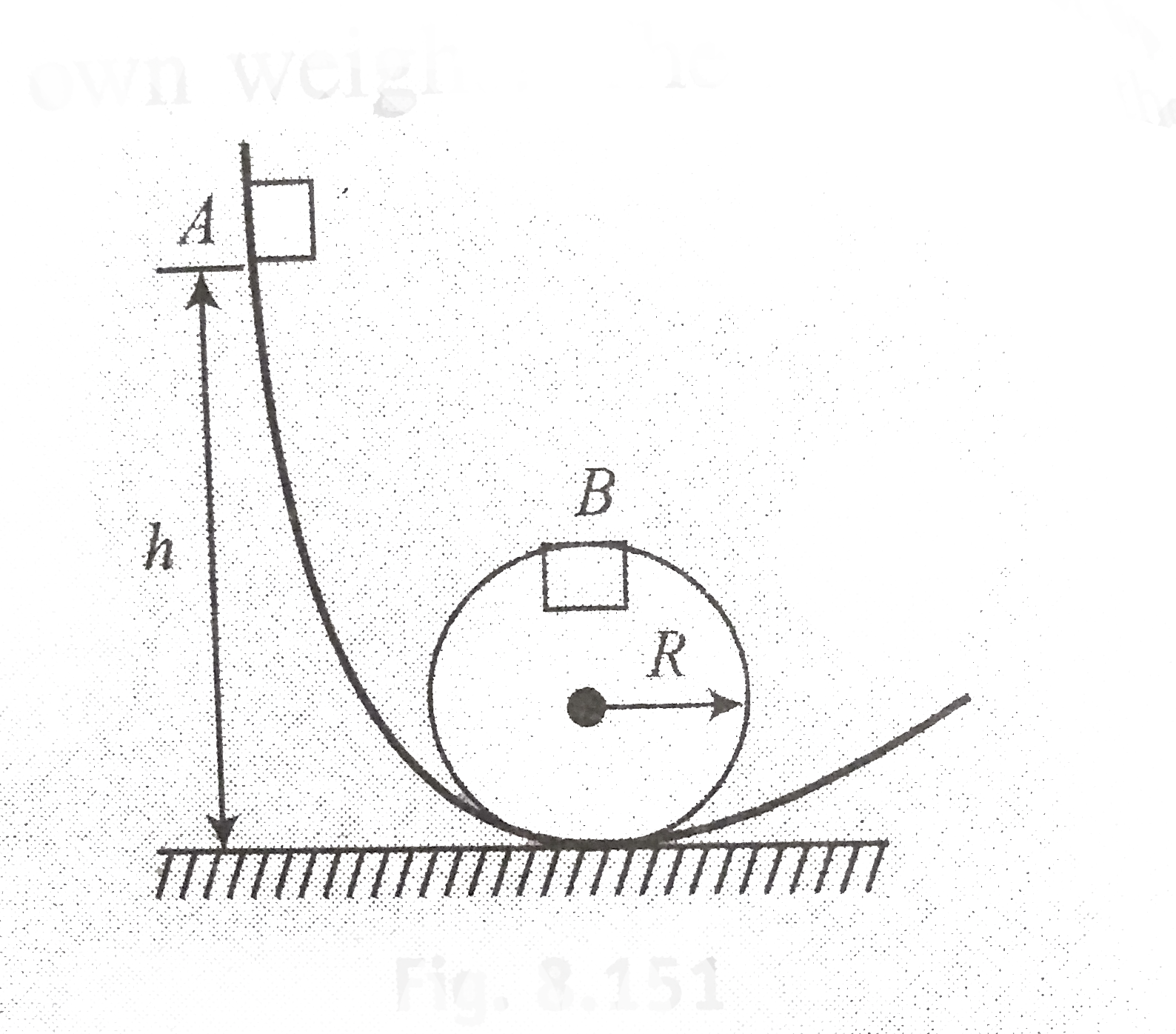
View Solution
Knowledge Check
An object of mass m is released from rest at a height h above the surface of a table. The object slides along the inside of the loop. The loop track consisting of a ramp and a circular loop of radius R shown in the figure. Assume that the track is frictionless. When the object is at the top of the circular track it pushes against the track with a force equal to three times its weight. What height was the object dropped from?
 A3RB4RC5RD6R
A3RB4RC5RD6RA block of mass m starts from rest and slides down a frictionless semi-circular track from a height h as shown. When it reaches the lowest point of the track, it collides with a stationary piece of putty also having mass m. If the block and the putty . stick together and continue to slide, the maximum height that the block-putty system could reach is
 Ah4Bh2ChDindependent of h
Ah4Bh2ChDindependent of hA block of mass m sits at rest on a frictionless table in a rail car that is moving with speed vc along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force F for a time t in the direction of the car's motion.
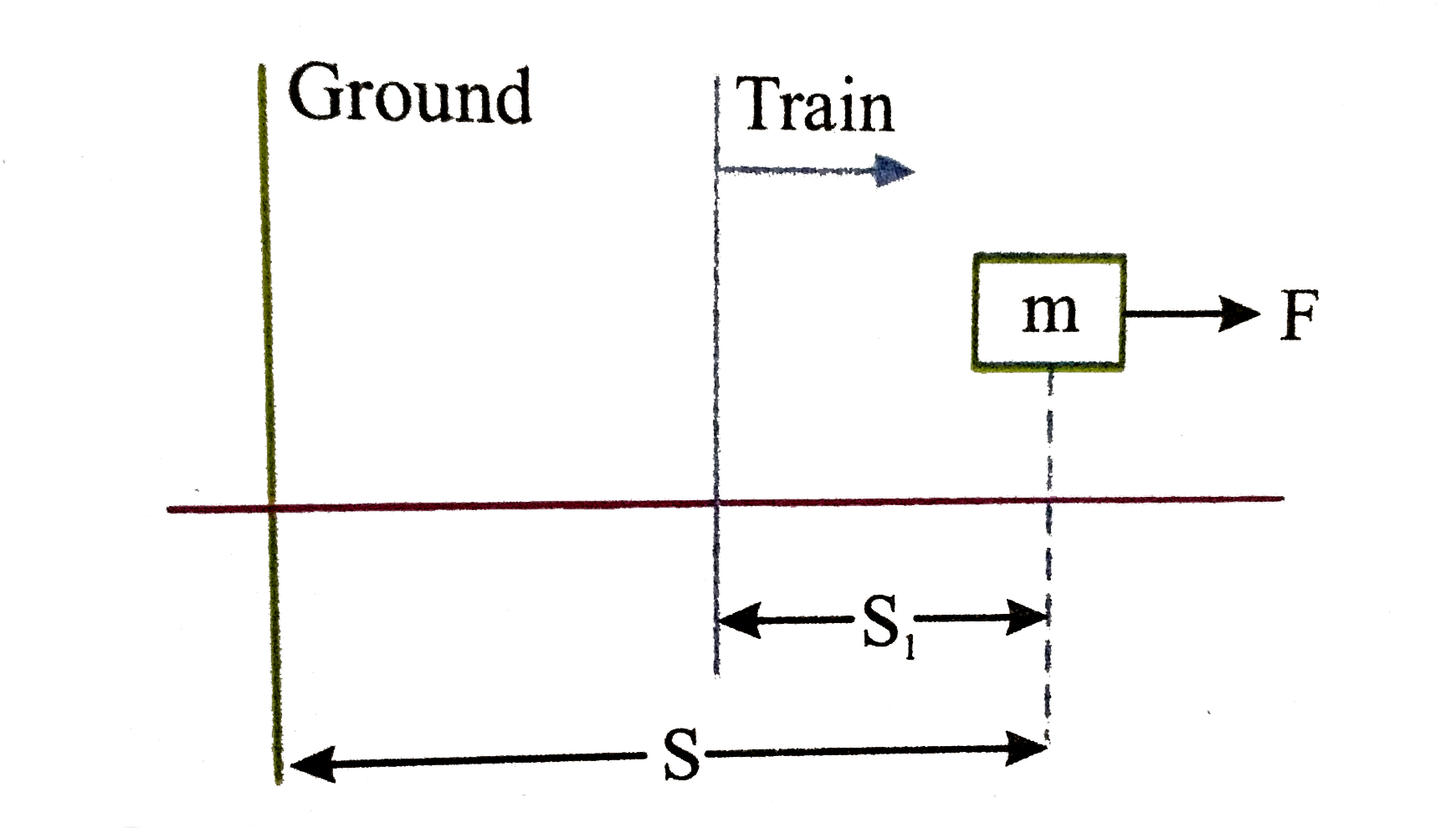
What is the final speed of the block according to a person in the car ?AFtmB2FtmC−FtmDzero
Figure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

View SolutionA block of mass m sits at rest on a frictionless table in a rail car that is moving with speed vc along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force F for a time t in the direction of the car's motion.
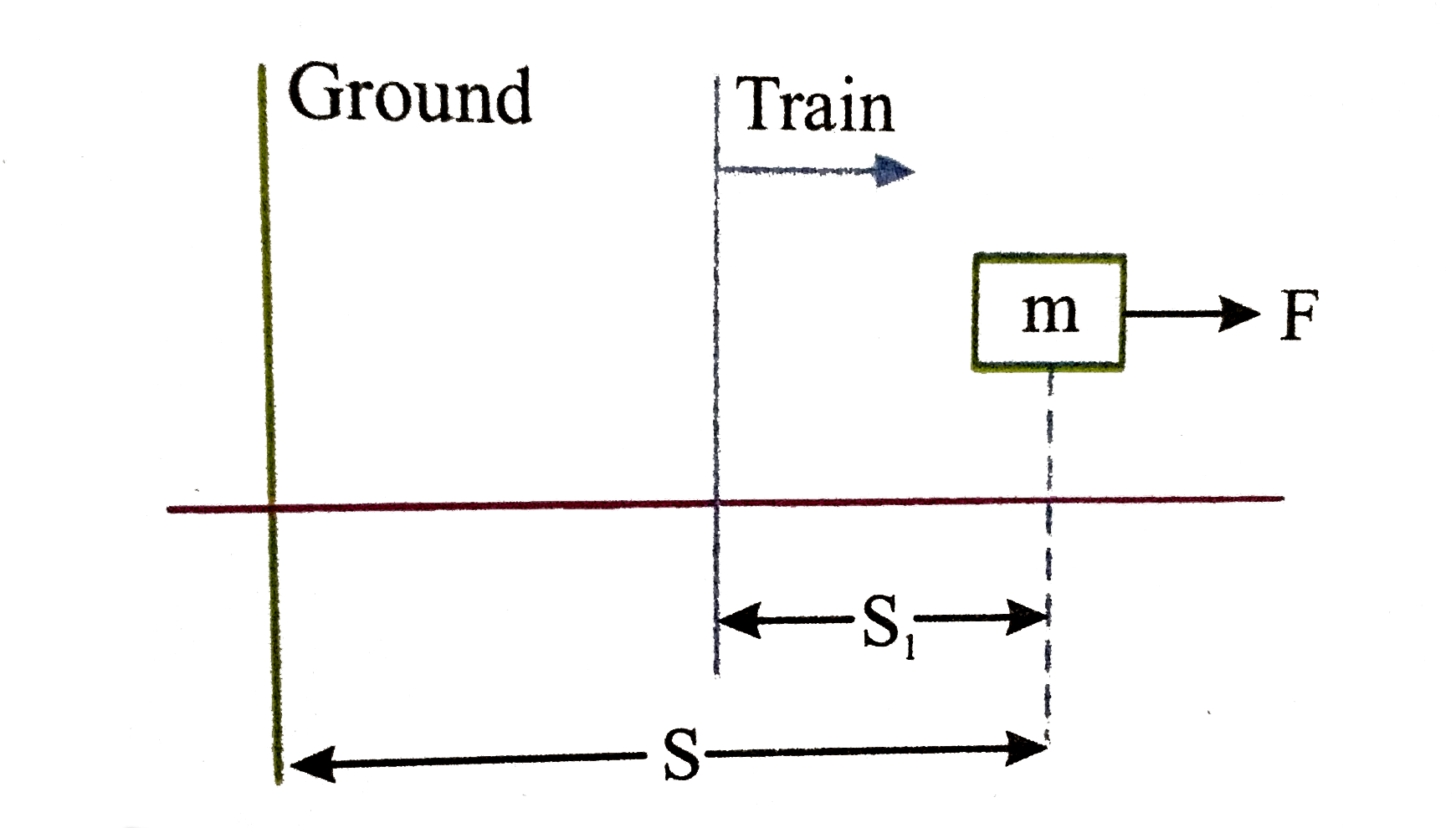
According to a person standing on the ground outside the train ?
View SolutionA block of mass m sits at rest on a frictionless table in a rail car that is moving with speed vc along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force F for a time t in the direction of the car's motion.
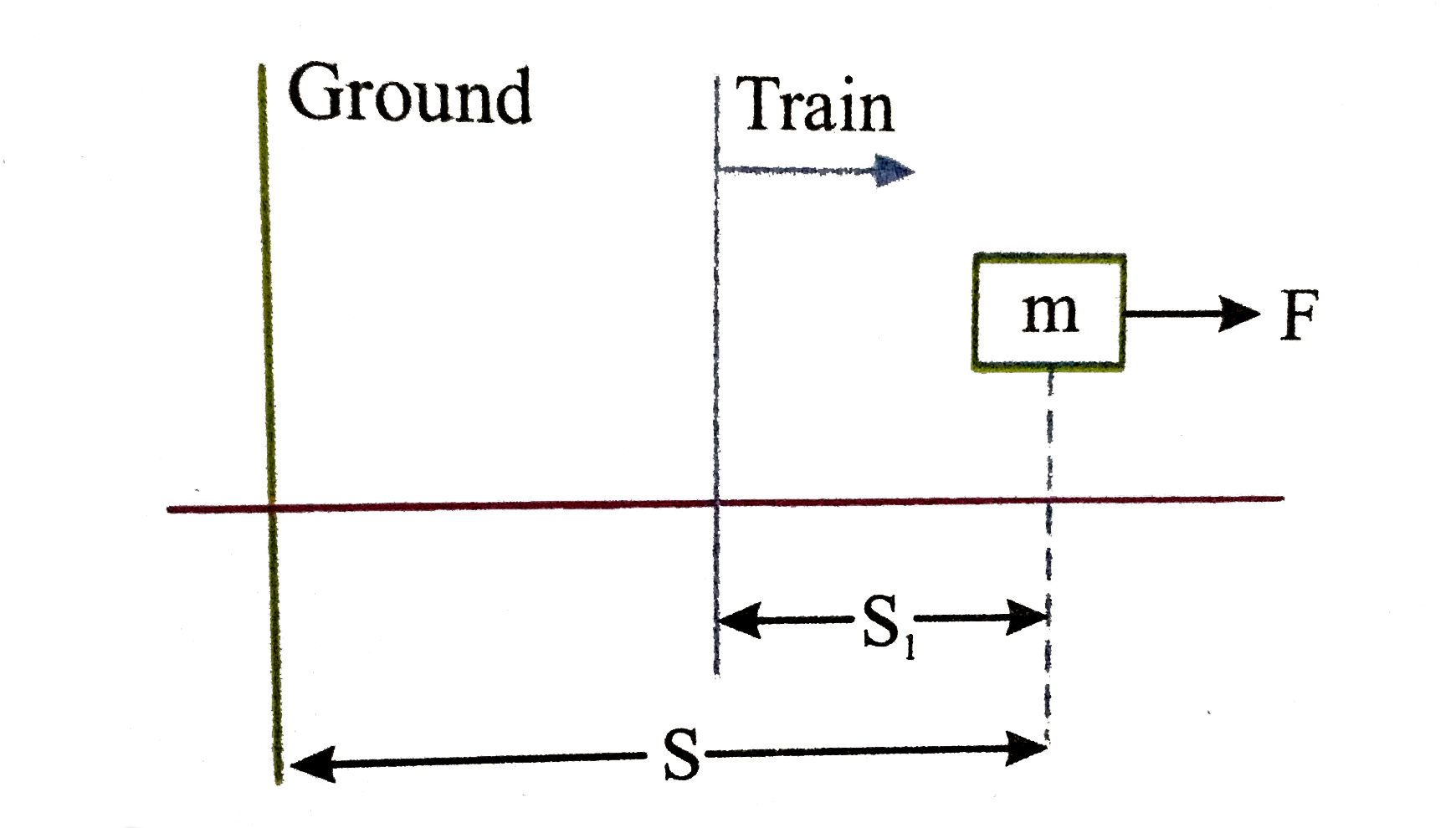
According to the person on the ground. The change in KE of block is
View SolutionA block of mass m sits at rest on a frictionless table in a rail car that is moving with speed vc along a straight horizontal track (fig.) A person riding in the car pushes on the block with a net horizontal force F for a time t in the direction of the car's motion.
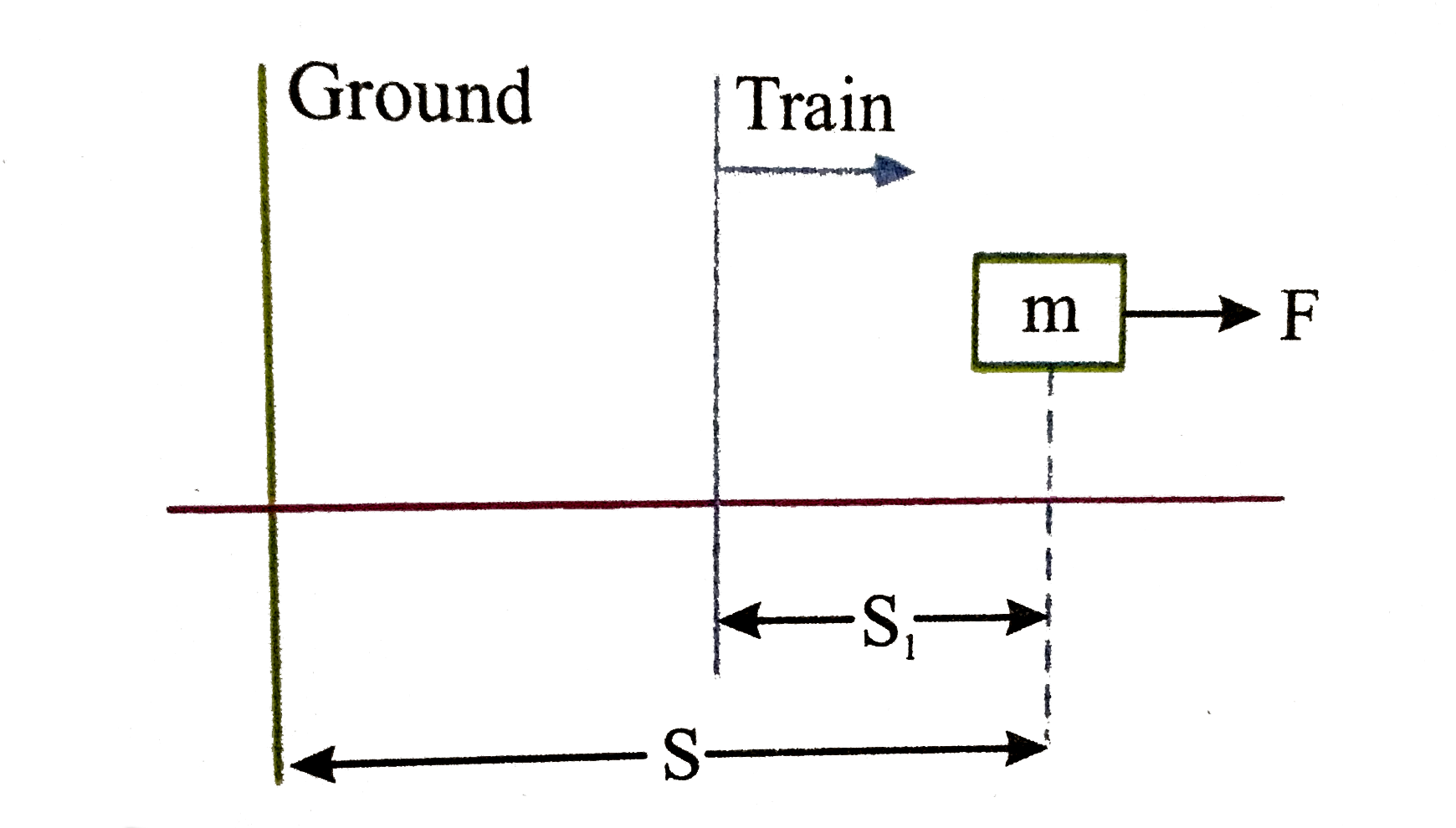
According to the person on the ground. The displacement of block is
View SolutionIn the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is
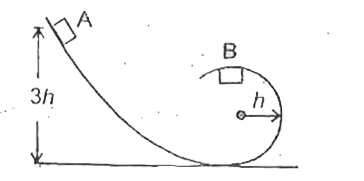
View Solution
