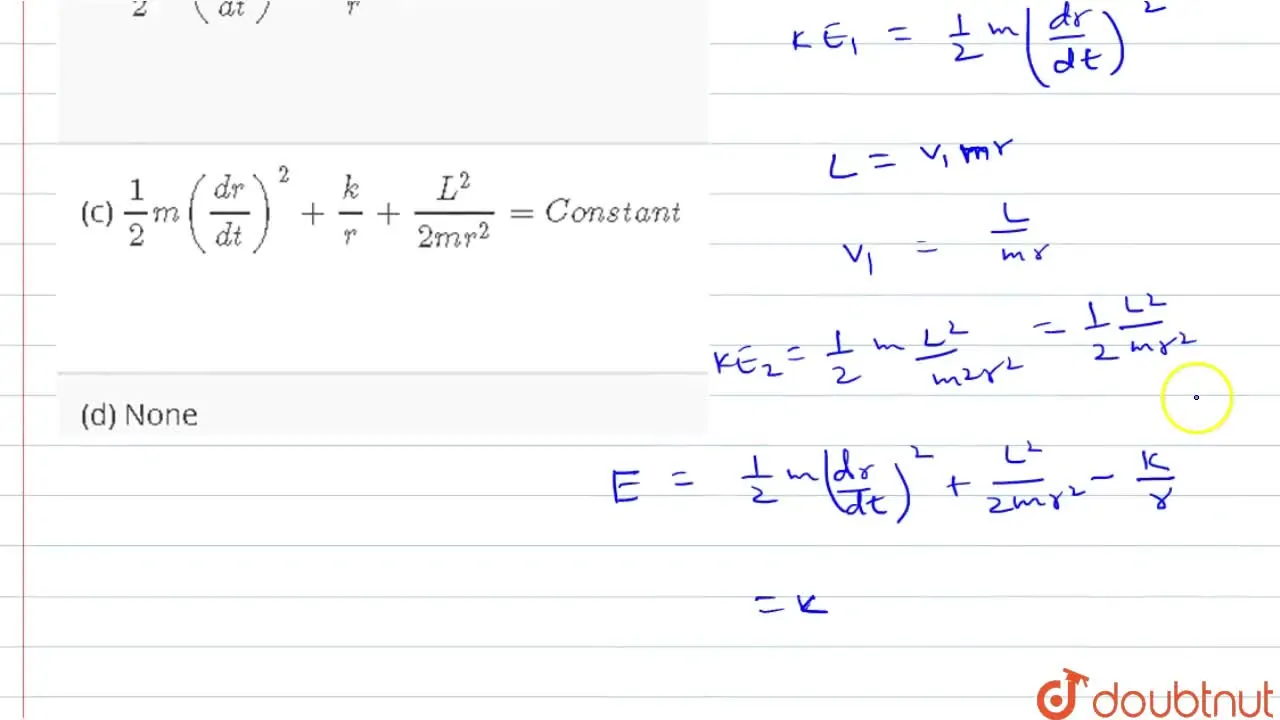Let r be the distance of a particle from a fixed point to which it is attracted by an inverse square law force given by F=k/r2 (k=constant). Let m be the mass of the particle and L be its angular momentum with respect to the fixed point. Which of the following formulae is correct about the total energy of the system?
(a) 12m(drdt)2−kr+L2mr2=Constant
(b) 12m(drdt)2−kr=Constant
(c) 12m(drdt)2+kr+L22mr2=Constant
(d) None
The correct Answer is:A
F=kr2
U=−∫→F.d→r=−∫→Fd→rcosπ
∫Fdr=kr2dr=−kr, V2=radialvelocity=drdt
Hence, KE due to this velocity =12(drdt)2m
V1= tangential velocity and mV1r=L
∴V1=Lmr
KE due to tangential velocity =12mv21
(Lmr)2mV21=12mL2m2r2=12L2mr2
Total energy =KEtotal+PE
=12m(drdt)2+12L2mr2−kr
Related Playlists
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
A particle with position vector has a linear momentum p. Which of the following statements is true in respect of its angular momentum L about the origin?
View SolutionA particle with the position vector r has linear momentum p. Which of the following statements is true is respect of its angular momentum L about the origin ?
View SolutionA particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to (−K/r2), where k is a constant. The total energy of the particle is -
View SolutionA particle of mass m is moving in a horizontal circle of radius R under a centripetal force equal to −Ar2 (A = constant). The total energy of the particle is :-
(Potential energy at very large distance is zero)View SolutionThe reference frame, in which the centre of inertia of a given system of particles is at rest, translates with a velocity V relative to an inertial reference frame K. The mass of the system of particles equals m, and the total energy of the system in the frame of the centre of inertia is equal to ˜E. Find the total energy E of this system of particles in the reference frame K.
View SolutionA particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to (−K/r2), where k is a constant. The total energy of the particle is -
View SolutionPotential energy of a system of particles is Uα3r3−β2r2, where r is distance between the particles. Here αandβ are positive constants. Which of the following are correct for the system?
View SolutionThe potential energy of a two particle system separated by a distance r is given by U(r)=Ar where A is a constant. Find to the radial force Fr, that each particle exerts on the other.
View SolutionA moving in which the distance fo the moving particle from a fixed point is always constant during motion is called………………………… .
View SolutionA particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical circular path about its other end. The minimum speed of the particle at its highest point must be
View Solution