Block is hanging from vertical spring of spring constant and is rest. Block strikes block with velocity and sticks to it. Then the value of for which the spring just attains natural length is
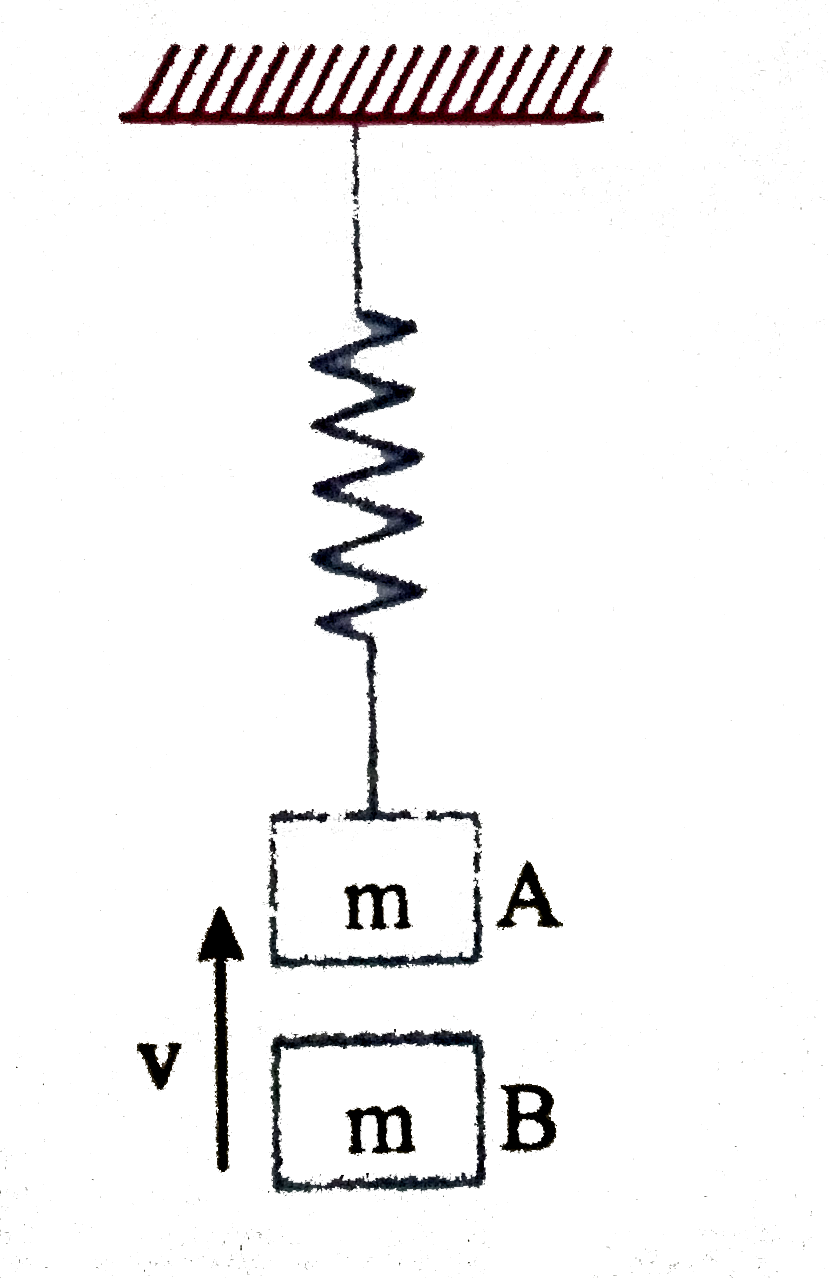
(a)
(b)
(c)
(d) None of the above
The correct Answer is:B
The initial extension in spring is
Just after collision of B with A, the speed of the combined mass is . For the spring to just attain natural length, the combined mass must rise up by and come to rest.

Applying conservation of energy between initial and final states,
Solving, we get
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension
55 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
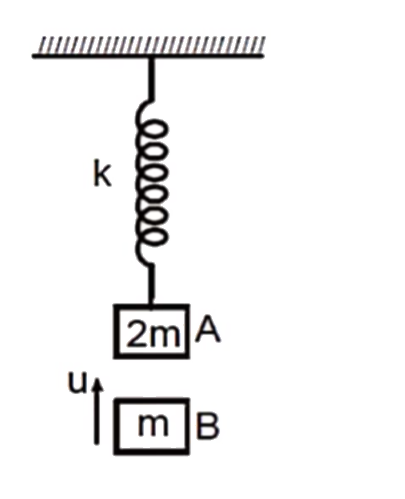
A block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
View SolutionThe ball strikes the block and sticks to it. Find the maximum compression of spring. (L: natural length of spring)

View Solution
Knowledge Check
Block A is hanging from a vertical spring and is at rest. Block B strikes the block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is
 A√60mg2kB√6mg2kC√10mg2kDnone of these
A√60mg2kB√6mg2kC√10mg2kDnone of theseBlock A is hanging from a vertical spring and is at rest. Block B strikes the block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is
 A√60mg2kB√6mg2kC√10mg2kD√8mg2k
A√60mg2kB√6mg2kC√10mg2kD√8mg2kTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
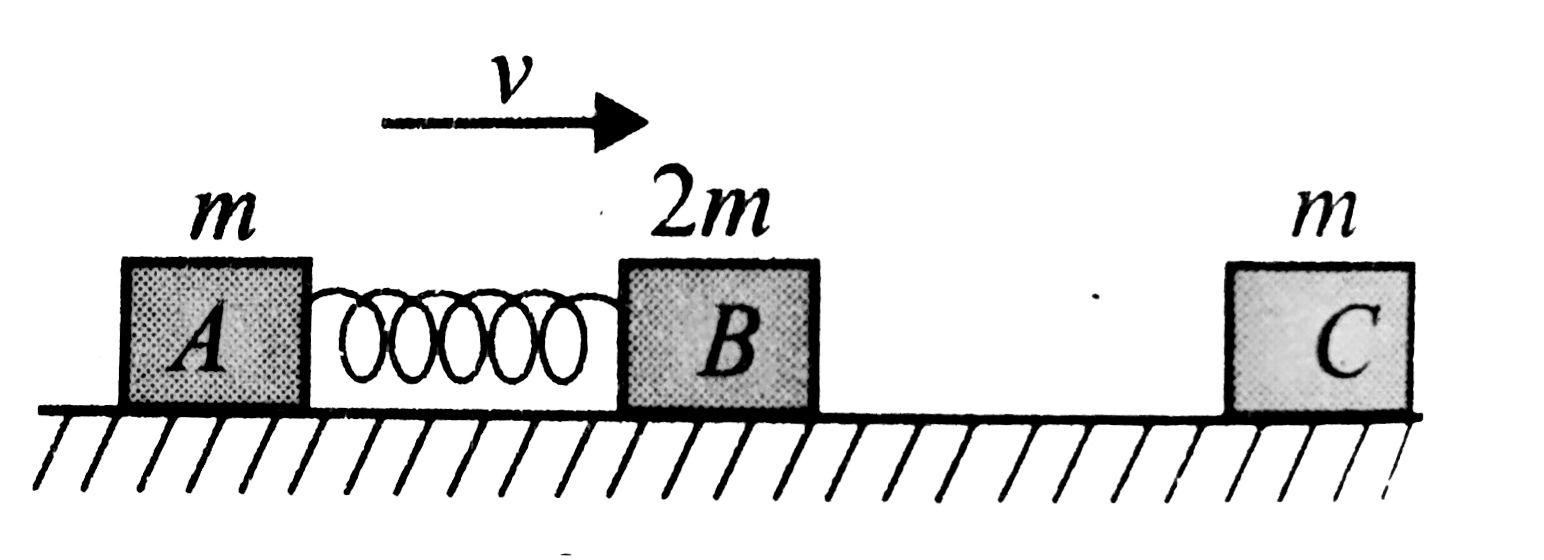 A√2mkBwill never be attainedC√m12kvD√m6kv
A√2mkBwill never be attainedC√m12kvD√m6kv
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.

View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
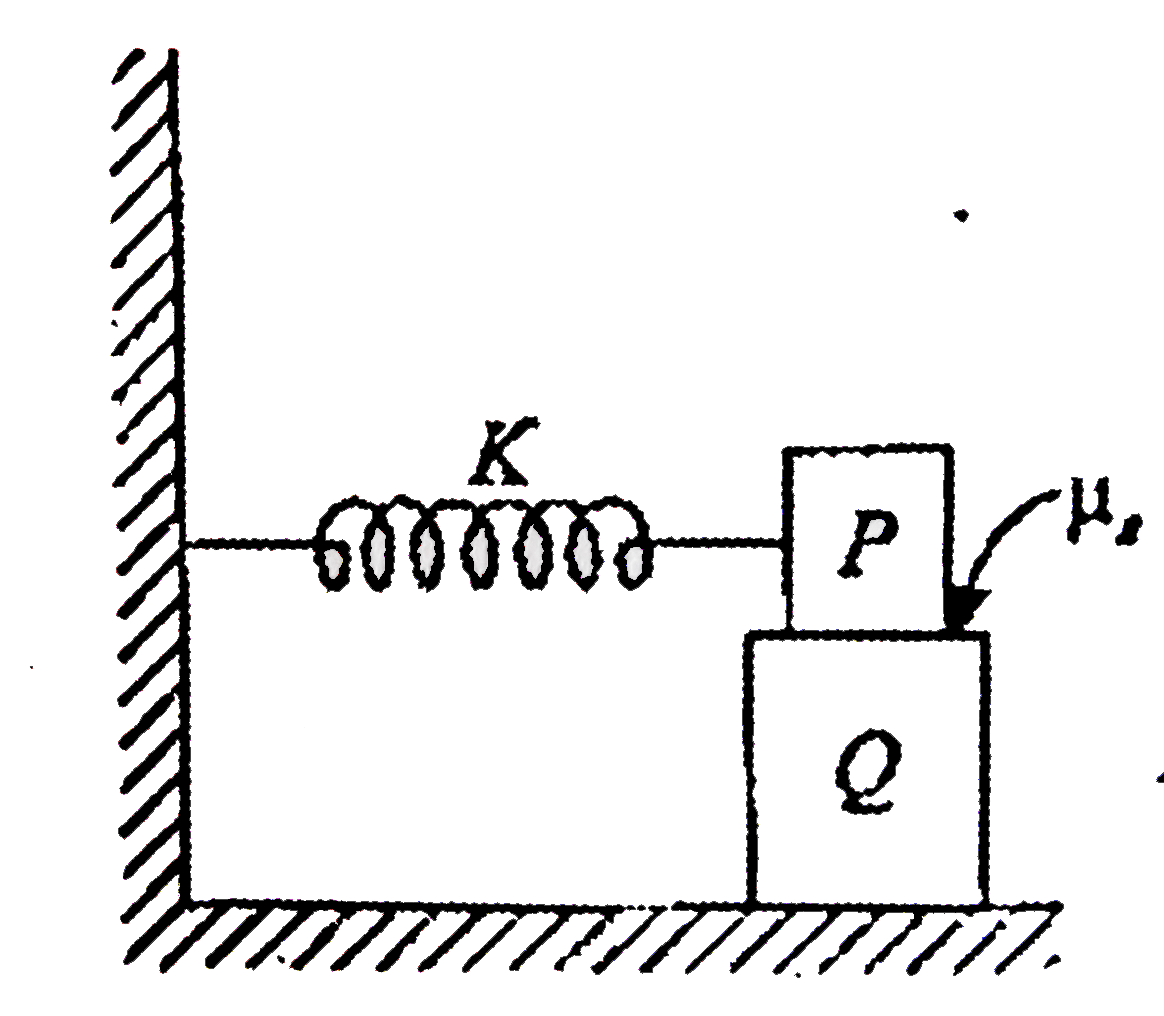
View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
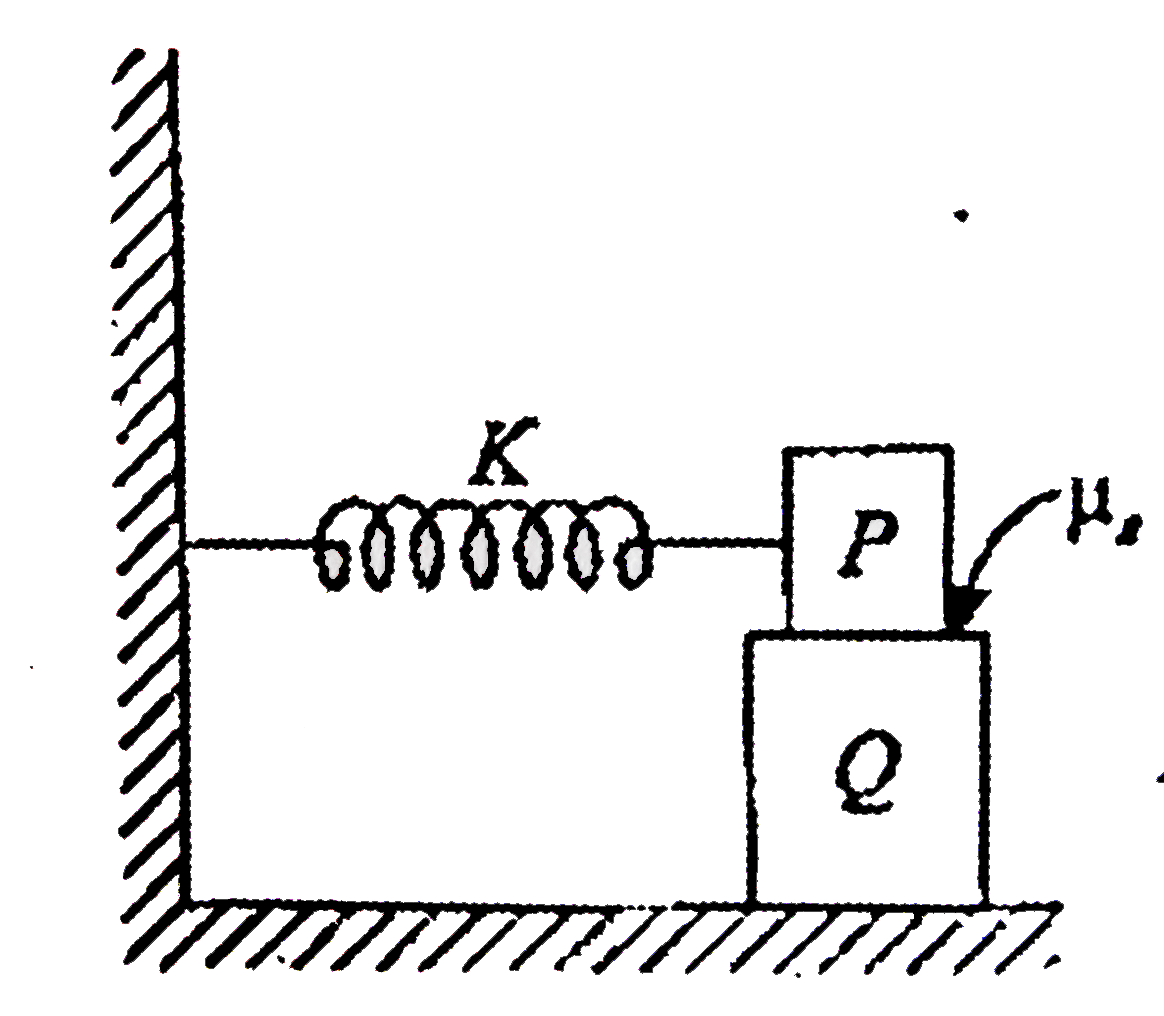
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View Solution
