At the moment t=0 particle leaves the origin and moves in the positive direction of the x-axis. Its velocity varies with time as . The dislpacement and distance in 8 second will be
16 m, 34 m
16 m, 25 m
16 m, 16 m
16 m, 9m
The correct Answer is:A
Displacement
To find the distance, first determine whether velocity becomes zero in the given time interval or not.

Distance
OR
Draw a v-t graph
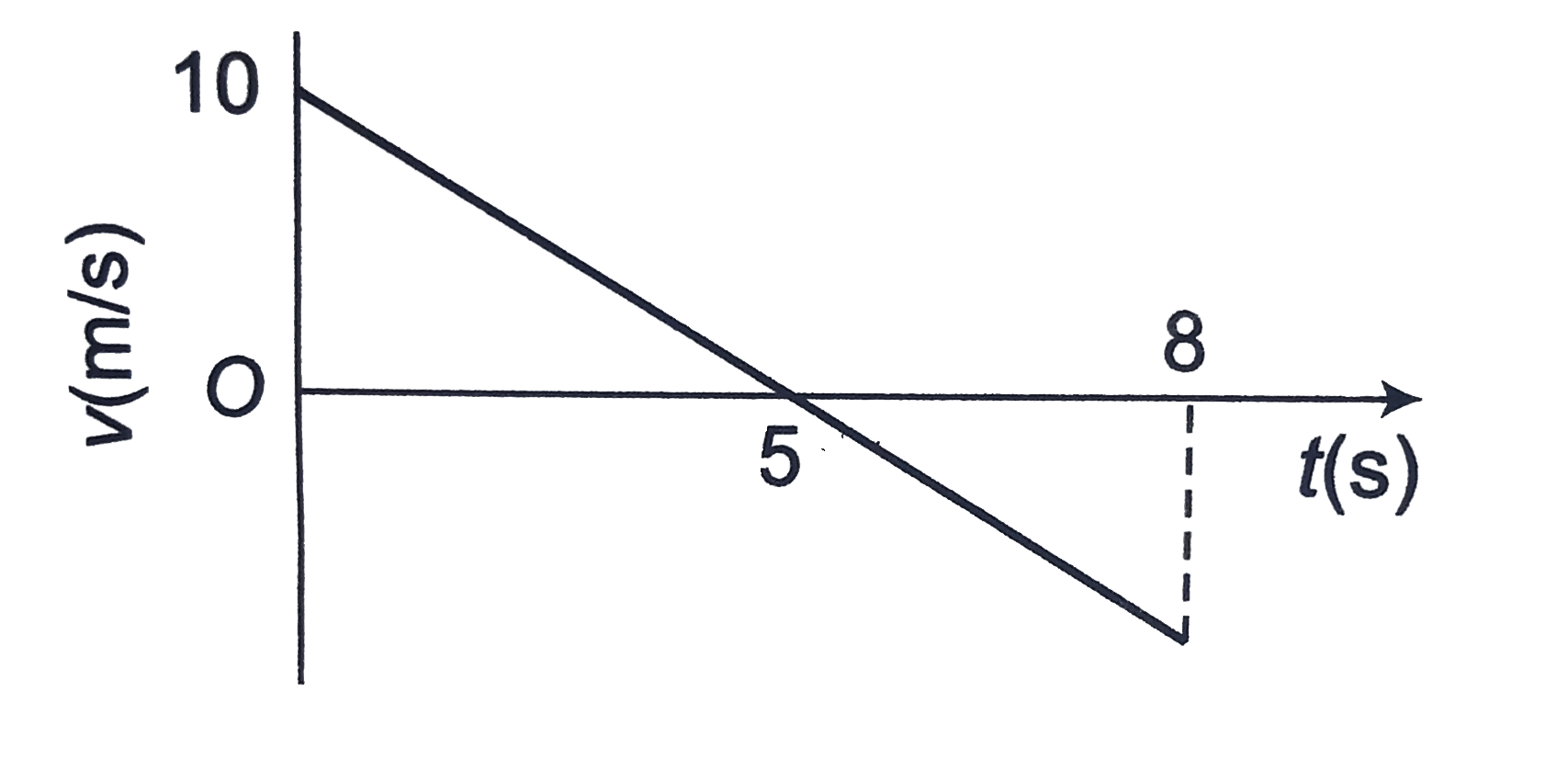
Area of v-t graph gives displacement and distance
Displacement
Distance
Topper's Solved these Questions
Similar Questions
At the moment t=0 a particle leaves the origin and moves in the positive direction of the x-axis. Its velocity varies with time as v=v0(1−t/τ), where v0 is the initial velocity vector whose modulus equals v0=10.0cm/s, τ=5.0s. Find:
(a) the x coordinate of the particle at the moments of time 6.0, 10, and 20s,
(b) the moments of time when the particles is at the distance 10.0cm from the origion,
(c) the distance s covered by the particle during the first 4.0 and 8.0s, draw the approximate plot s(t).
View Solution(a) At the moment t=0, a particle leaves the origin and moves in the positive direction of the x-axis. Its velocity is given by v=10−2t. Find the displacement and distance in the first 8s.
(b) If v=t−t2, find the displacement and distamce in first 2s.
View Solution
Knowledge Check
A particle located at x=0 at time t=0, starts moving along with the positive x−direction with a velocity 'v' that varies as v=a√x. The displacement of the particle varies with time as
At2BtCt12Dt3The velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
AThe initial velocity of the particle is zeroBthe initial velocity of the particle is 2.5ms.CThe accelration of the particle is 2.5ms2.DThe acceleration of the particle is 50ms2.A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=p√x. The displacement of the particle varies with time as (where, p is constant)
At3Bt2CtDt1/2
At the moment t=0 a particle leaves the origin and moves in the positive direction of the x-axis.Its velocity at any time is →v=→v0(1−tτ) where v0=10 cm/s and τ=5 s. Find :
(a)the x-coordinates of the particle at the instant 6s, 10s and 20s.
(b)the instant at which it is a distance 10 cm from the origin.
(c )the distance s covered by the particle during the first 4s and 8s.
View SolutionAcceleration of particle moving along the x-axis varies according to the law a=−2v, where a is in m/s2 and v is in m/s. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of time t.
(b) Find its position x as function of time t.
(c) Find its velocity v as function of its position coordinates.
(d) find the maximum distance it can go away from the origin.
(e) Will it reach the above-mentioned maximum distance?
View SolutionA particle located at "x=0" at time "t=0" starts moving along the positive "x" - direction with a velocity "v" that varies as "v=alpha sqrt(x)".The displacement "(x)" of the particle varies with time as "(alpha" is constant)
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
View SolutionAcceleration of a particle moving along the x-axis is defined by the law a=−4x, where a is in m/s2 and x is in meters. At the instant t=0, the particle passes the origin with a velocity of 2m/s moving in the positive x-direction.
(a) Find its velocity v as function of its position coordinates.
(b) find its position x as function of time t.
(c) Find the maximum distance it can go away from the origin.
View Solution
