Complete Solutions to COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) ) of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| MODERN PUBLICATION | COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) ) |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
A thin and uniform rod of mass M and length L is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping. Which of the following statement(s) is(are) correct, when the rod makes an angle 60° with vertical? [g is the acceleration due to gravity]
View SolutionThe potential energy of a particle of mass ? at a distance ? from a fixed point ? is given by `V(r)=kr^(2)//2`, where ? is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ? about the point ?. If ? is the speed of the particle and ? is the magnitude of its angular momentum about ?, which of the following statements is (are) true?
View SolutionA cylinder is kept at rest on a sufficiently rough horizontal surface. A horizontal constant force is applied at the centre of mass of cylinder.
View SolutionAngular impulse J is applied on a system which can rotate about an axis for which its moment of inertia is I. System is initially at rest.
View Solutionthere is a rod AB of uniform cross section and its centre is C. In which of the following case(s) centre of mass of the rod may lie at C.
View SolutionA sphere is rolling down on a sufficiently rough inclined surface.
View SolutionNet external force acting on a system of particle is not equal to zero. If velocity and acceleration of the centre of mass of the system of particles at some instant of time are found to be v and a respectively select possible option (s).
View SolutionThere are two inclined planes A and B of same dimensions. A is sufficiently rough but B is smooth A round shaped object is released from rest at the top point of inclined plane A and acceleration the object is found to be a, and v1 is the velocity of centre of object when it reaches the bottom. When the same process is repeated with B then corresponding values are found to be `a_(2) and v_(2)`.
View SolutionTwo particles of different masses are thrown simultaneously in air. Centre of mass of two balls while both are in mid air.
View SolutionBlock a of mass 4 kg is to be kept at rest against a smooth vertical wall by applying a force F as shown in figure. The force required is :- `(g=10m//s^(2))`

View SolutionIf there is no external force acting on a nonrigid body, which of the followhng quantities must remain constant?
View SolutionIf there is no external force acting on a nonrigid body, which of the followhng quantities must remain constant?
View SolutionA solid sphere is rolled on a rough surface and it is found that sphere stops after some time.
View SolutionA disc of mass m and radius r is rotating with angular velocity, on a frictionless horizontal plane about a vertical axis passing through its centre. A ring of same mass and radius is gently placed on it in such a way that centres of both coincide. After some time it is found that both attain a common angular velocity
View SolutionTwo identical spheres `A` and `B` are free to move and I, rotate about their centres. They are given the same impel `J`. The lines of action of the impulses pass through tht centre of `A` and away from the centre of `B`, then
View SolutionA sphere and a block both are released from rest at the top of an inclined plane. After some time they reach the bottom. For all the options assume that angle made by the plane with the horizontal is more than angle of repose.
View SolutionConsider a body of mass 1.0 at rest at the origin at time `t = 0`. A force `vec F=(alpha t hat l +beta hat J) ` is applied on the body, where `alpha =1.0 Ns^(-1) and beta =1.0 N`. The torque acting on the body about the origin at time `t=1.0 s " is " vec tau` . Which of the following statements is (are) true?
View SolutionState of the sphere at some instant of time is shown in figure. Surface below the sphere is rough. At the given instant, speed of the centre of the sphere is u and angular velocity about the centre is u/2r. Select correct statement (s)
View SolutionA ring performs pure rolling on a horizontal surface and its state at some instant of time is shown in figure.
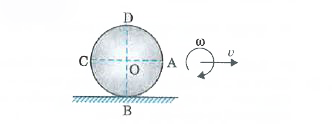
View SolutionTwo solid spheres P and Q are released from rest from the same point on an inclined plane. Plane is sufficiently rough to provide pure rolling Mass of P is greater than the mass of Q whereas radius of Q is greater than the radius of P
View SolutionA solid cylinder is rolling down the inclined plane without slipping. Which of the following isare correct?
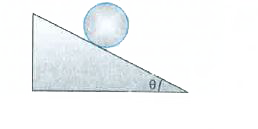
View SolutionThe position vector `vec(r)` of a particle of mass m is given by the following equation `vec(r) (t) = at^(3) hat(i) + beta t ^(2) hat(j) " where " alpha = 10//3 ms^(-3),beta = 5 ms^(-2) and m = 0 . 1 kg ` . At t = 1 s, which of the following statement (s) is (are) true about the particle ?
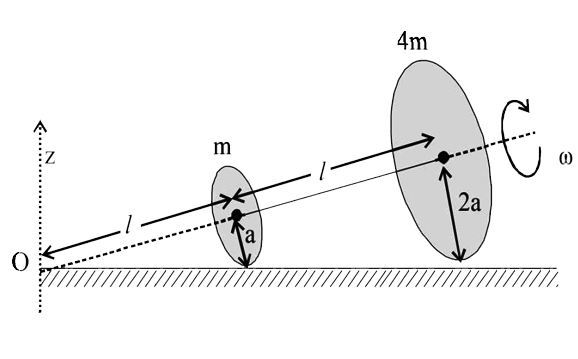
View SolutionTwo thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length `l= sqrt(24a)` through their centres. This assembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is `omega.` The angular momemtum of the entire assembly about the point 'O' is `vacL` (see the figure). Which of the follwing statement (s) is (are) true?
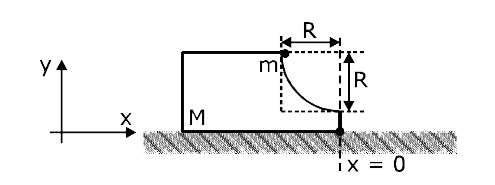
View SolutionA block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct?
View SolutionSphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

What will be the approximate velocity of combined system after the collision?
View SolutionSphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
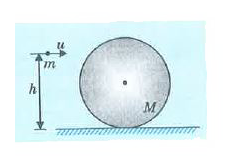
Angular velocity of the sphere just after the collision is
View SolutionSphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
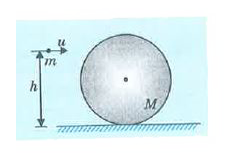
At what height h above the floor, particle should hit the sphere so that it may start pure rolling after the collision.
View SolutionSmall sphere of mass m and radius r is kept on fixed inclined rough surface. Surface makes an angle with the horizontal. Initially centre of sphere is at a height h above the horizontal floor. Coefficient of friction between the sphere and surface is u. Sphere is released from the state of rest.
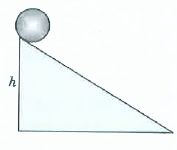
Assume that friction is sufficiet enough to provide pure rolling. Speed of the sphere as it reaches the bottom is
View SolutionSmall sphere of mass m and radius r is kept on fixed inclined rough surface. Surface makes an angle with the horizontal. Initially centre of sphere is at a height h above the horizontal floor. Coefficient of friction between the sphere and surface is u. Sphere is released from the state of rest.
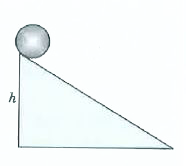
Assume that friction is sufficient engough for pure rolling. Accleeration of the shpere is
View SolutionSmall sphere of mass m and radius r is kept on fixed inclined rough surface. Surface makes an angle with the horizontal. Initially centre of sphere is at a height h above the horizontal floor. Coefficient of friction between the sphere and surface is u. Sphere is released from the state of rest.
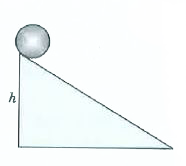
Assume friction is not sufficient to provided pure rolling. Acceleration of the sphere is
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here r is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assuming coefficient of friction between sphere and the surface. Mass of sphere is m.
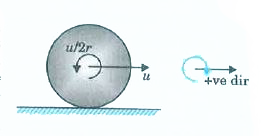
At what time sphere stops rotating for a moment?
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
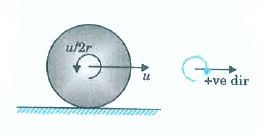
At what time sphere starts pure rolling?
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
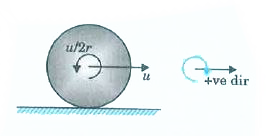
What will be the speed of sphere when it starts pure rolling?
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity `omega` is an example of non=inertial frame of reference. The relationship between the force `vecF_(rot)` experienced by a particle of mass m moving on the rotating disc and the force `vecF_(in)` experienced by the particle in an inertial frame of reference is
`vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega`.
where `vecv_(rot)` is the velocity of the particle in the rotating frame of reference and `vecr` is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed `omega` about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis `(vecomega=omegahatk)`. A small block of mass m is gently placed in the slot at `vecr(R//2)hati` at `t=0` and is constrained to move only along the slot.
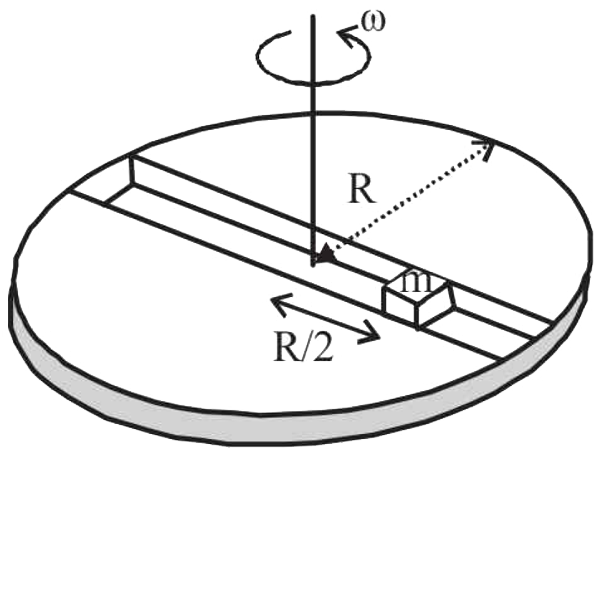
The distance r of the block at time is
View SolutionA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity `omega` is an example of non=inertial frame of reference. The relationship between the force `vecF_(rot)` experienced by a particle of mass m moving on the rotating disc and the force `vecF_(in)` experienced by the particle in an inertial frame of reference is
`vecF_(rot)=vecF_(i n)+2m(vecv_(rot)xxvec omega)+m(vec omegaxx vec r)xxvec omega`.
where `vecv_(rot)` is the velocity of the particle in the rotating frame of reference and `vecr` is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed `omega` about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis `(vecomega=omegahatk)`. A small block of mass m is gently placed in the slot at `vecr(R//2)hati` at `t=0` and is constrained to move only along the slot.
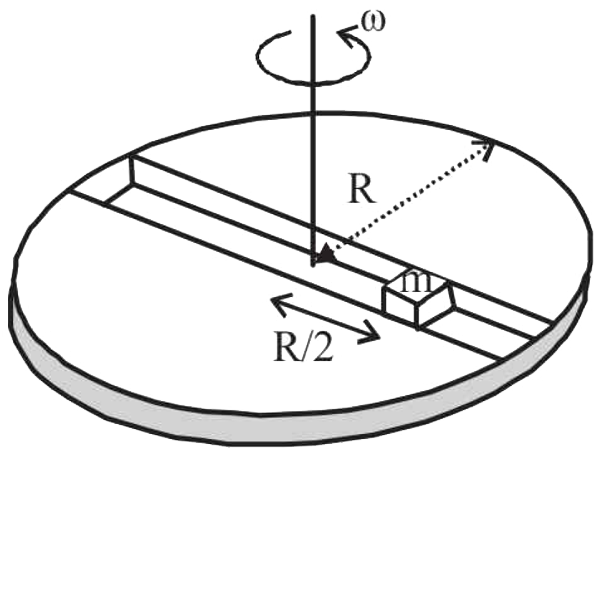
The net reaction of the disc on the block is
View Solution
COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) ) questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- Chapter Practice Test (for Board Examination)
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
- Conceptual Questions
- HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL QUESTIONS WITH ANSWERS
- NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
- NCERT FILE ( NCERT TEXTBOOK EXERCISES )
- NCERT FILE (NCERT EXEMPLAR PROBLEMS (OBJECTIVES QUESTIONS) (MULTIPLE CHOICE QUESTIONS (TYPE-I))
- NCERT FILE (NCERT EXEMPLAR PROBLEMS (SUBJECTIVES QUESTIONS) (Very Short Answer Type Questions))
- PRACTICE PROBLEMS
- PROBLEMS TOUGH & TRICKY
- REVISION EXERCISES (Additional Questions Carrying 1 mark )
- REVISION EXERCISES (Fill in the Blanks Carrying 1 mark )
- REVISION EXERCISES (Long Answer Questions Carrying 5 marks)
- REVISION EXERCISES (Numerical Problems)
- REVISION EXERCISES (Short Answer Questions Carrying 2 or 3 marks)
- REVISION EXERCISES (Very Short Answer Questions Carrying 1 mark)
- SOLVED EXAMPLES