Complete Solutions to COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) ) of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| MODERN PUBLICATION | COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) ) |
| Number Of Questions | 67 |
| Academic Year | 2023-24 |
A large number of particles are placed around the origin, each at a distance R from the origin. The distance of the center of mass of the system from the origin is
View SolutionA sphere of radius 1 m is kept on a plank kept on horizontal surface. Accelerations of plank and centre of sphere are indicated in the figure.

If sphere is not slipping on the plank then its angular acceleration is
View SolutionConsider the following two statements:
A. Linear momentum of a system of partcles is zero.
B. Kinetic energ of a system of particles is zero.
View SolutionThe radius of gyration of an uniform rod of length `L` about an axis passing through its centre of mass and perpendicular to its length is.
View SolutionA particle of mass m is moving on the XY-plane along a straight line y = d, with constant velocity v. Its angular momentum about the origin
View SolutionA person is sitting on a rotating chair which is rotating with some angular velocity. Person is sitting on the chair with his arms folded. Now he slowly stretches his arm then
View SolutionA uniform rod is kept vertically on a horizontally smooth surface at a point O. IF it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
View SolutionA ring performs pure rolling on a horizontal fixed surface with its centre moving with speed v.
View SolutionIn above question, what will be the speed of the particle on the ring which is at the same height as that of the centre?
View SolutionFour identical rods each of mass `m` and length `l` are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
View SolutionA block of mass m is sliding down an inclined plane with uniform velocity v. Angle that the plane makes with the horizontal is `theta`. Assume edge of the cube to be a, calculate torque of the normal reaction about the centre of the block.
View SolutionTwo particles of masses `m_1 and m_2` are joined y a light rigid rod of length r. The system rotates at an angular speed `omega` about an axis through the centre of mass of the systemand perpendicular to the rod. Shwo thast the angular momentum of the system `is L=mur^2omega where mu` is the reduced mass of the system defined as `mu=(m_1m_2)/(m_1+m_2)`
View SolutionA solid sphere, disc and hollow sphere are placed at the top of an inclined plane. Surface is sufficiently rough to provide pure rolling. All the objects are released from a state of rest
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
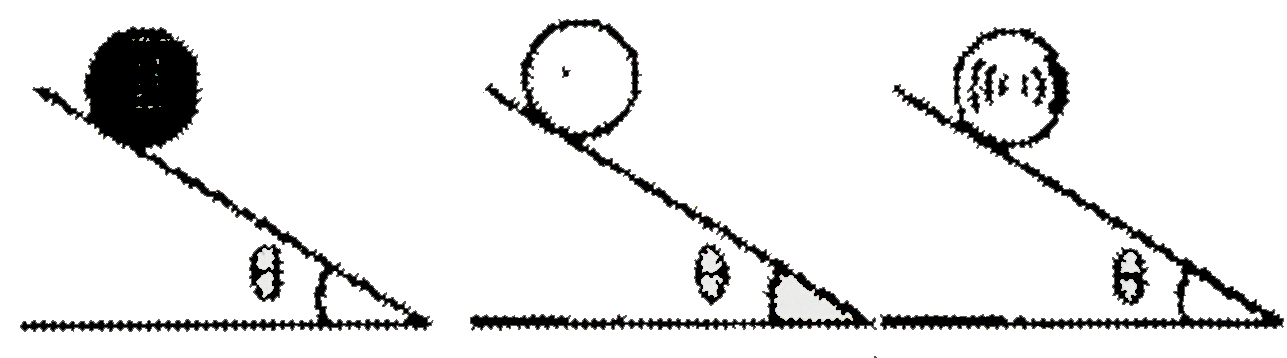
Which of the follwing order is true for final `KE` of the bodies?
View SolutionA solid sphere, disc and hollow sphere of same masa and radius are placed at the top of an inclined plane. Surface is sufficiently rough to provide pure rolling. All the objects are released from a state of rest.
View SolutionA large trolley is kept at rest on a frictionless horizontal surface. There are same peple standing on the trolley. Initially no one is moving.` C_(1)` is centre of mass of trolley and `C_(2)` is centre of mass of trolley plus people. Now people start moving on the trolley.
View SolutionLet `I_(A)` and `I_(B)` be moments of inertia of a body about two axes `A` and `B` respectively. The axis `A` passes through the centre of mass of the body but `B` does not. Then
View SolutionTwo' blocks of masses m, and m, are connected to the two ends of a string passing over a pulley as shown in figure. System hans vertically and blocks are held at rest. Assume that `m_(1) gt m_(2)`. Find the speed attained by the blocks when m, descends through a height h. Moment of inertia of the pulley is I and its radius is r. There is enough friction between string and pulley so that there is no slipping between them.
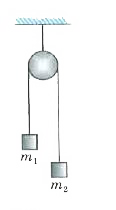
View SolutionIn which of the following cases it is certainly not possible for the diac to perform pure rolling.
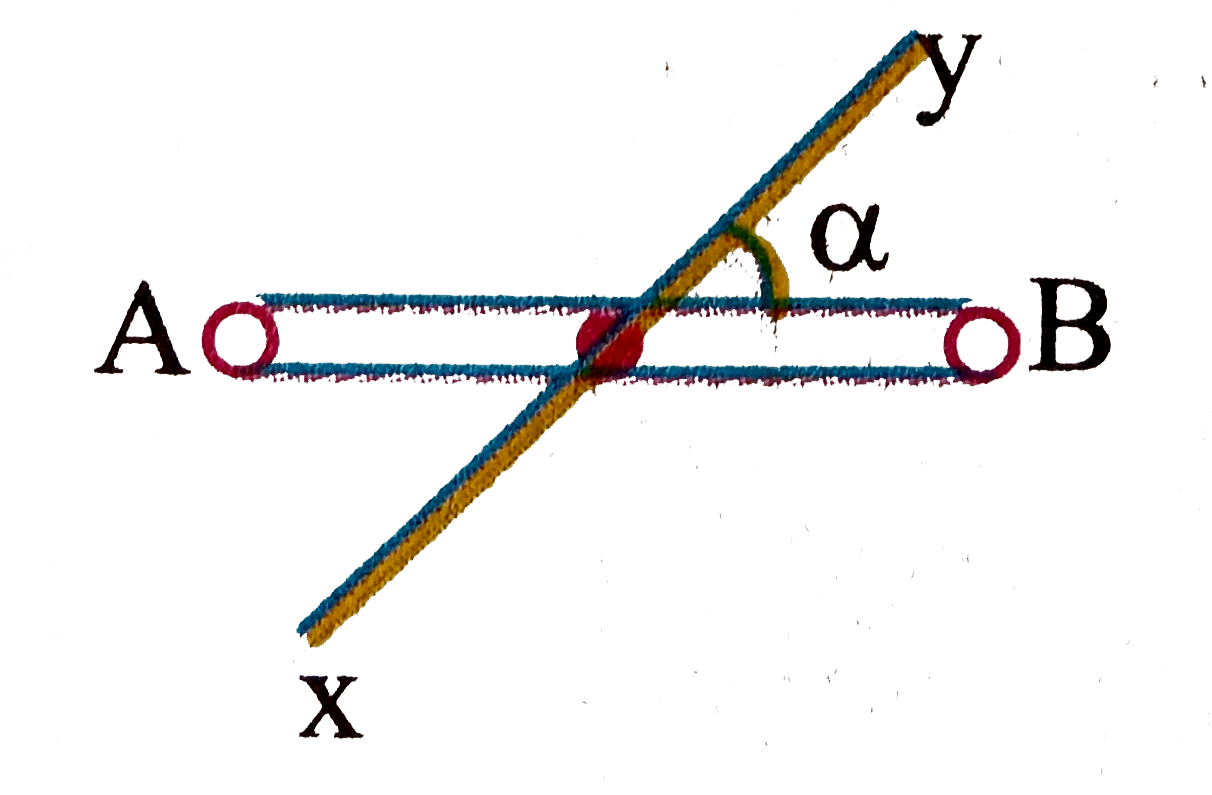
View SolutionThe moment of inertia of a uniform rod of length `2l` and mass `m` about an axis `xy` passing through its centre and inclined at an enable `alpha` is
View SolutionMotion of the rigid body is observed from an inertial frame of reference. Rigid body is rotating with constant angular speed about a fixed vertical axis. If we consider a particle of the rigid body not lying on its axis of rotation then net force acting on this particle is.
View SolutionMotion of the rigid body is observed from an inertial frame of reference. Rigid body is rotating with nonuniform angular speed about a fixed vertical axis. If we consider a particle of the rigid body not lying on its axis of rotation then net force acting on this particle is
View SolutionIf the radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionA particle is going around in a circular path with constant speed. Angular momentum of particle is conserved about
View SolutionThe direction of the angular velocity vector is along
View SolutionThe moments of inertia of two rotating bodies A and B are `I_(A)` and `I_(B). (I_(A) gt I_(B))` and their angular momenta are equal. Which one has greater `K.E.` ?
View SolutionA solid sphere rolls on a table without any slipping. What is the fraction of total K.E. associated with rotational K.E.?
View SolutionThere is a solid sphere of mass m. Moment of inertia about the axis passing through the centre of sphere is I. If the material of the sphere is recast to a disc of same radius then what would be its moment of inertia?
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionThere is a square planar object. Moment of inertia of this object about an axis passing through its centre and parallel to its edge is I. What will be moment of inertia about one of its diagonals?
View SolutionA solid sphere is rotating freely about its symmetry axis in free space. The radius of the sphere is increased keeping its mass same. Which of the following physical quantities would remain constant for the sphere?
View SolutionA solid sphere of radius `R` is placed on a smooth horizontal surface. A horizontal force `F` is applied at height `h` from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA circular disc is to be made by using iron and aluminium, so that it acquires maximum moment of inertia about its geometrical axis. It is possible with
View SolutionThree objects, A (a solid sphere), B (a thin circular disc) and C (a circular ring), each have the same mass M and radius R. They all spin with the same angular speed `omega` about their own symmetry axes. The amounts of work (W) required to bring them to rest, would satisfy the relation
View SolutionA solid sphere (mass 2M) and a thin spherical shell (mass M) both of the same size roll down an inclined plane, then:
View SolutionIf the earth were to suddenly contract to half of its present radius (without any external torque on it), by what duration would the day be decreased ? Assume earth to be perfect solid sphere of radius `(2)/(5)MR^(2)`.
View SolutionA solid sphere is in rolling motion. In rolling motion a body prosseses translational kinetic energy `(K_(t))` as well as rotational kinetic energy `(K_(r))` simutaneously. The ratio
`K_(t) : (K_(t) + K_(r))` for the sphere is
View SolutionA solid cylinder of mass 2 kg and radius 50 cm rolls up an inclined plane of angle of inclination `30^(@)`. The centre of mass of the cylinder has speed of 4 m/s. The distance travelled by the cylinder on the inclined surface will be, [ take `g=10m//s^(2)]`
View SolutionA thin rod of length `L` and mass `M` is bent at its midpoint into two halves so that the angle between them is `90^@`. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is.
View Solutioncricket bat is cut at the location of its centre of mass as shown in the fig. Then

View SolutionFour identical thin rods each of mass `M` and length `l`, from a square frame. Moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is
View SolutionIf is the force acting on a particle having position vector and be the torque of this force about the origin, then-
View SolutionThe moment of the force, `vec F = 4 hati + 5 hat j - 6 hat k` at `(2, 0 , - 3)`. About the point `(2, - 2, -2)` is given by
View SolutionTwo particle which are initially at rest move towards each other under the action of their internal attraction. If their speeds are `v` and `2 v` at any instant, then the speed of centre of mass of the system will be
View SolutionA circular disc of moment of inertia `I_(t)` is rotating in a horizontal plane about its symmetry axis with a constant angular velocity `omega_(i)`. Another disc of moment of inertia `I_(b)` is dropped co-axially onto the rotating disc. Initially, the second disc has zero angular speed. Eventually, both the discs rotate with a constant angular speed `omega_(f)`. Calculate the energy lost by the initially rotating disc due to friction.
View SolutionFrom a given sample of uniform wire, two circular loops `P` and `Q` are made, `P` of radius `r` and `Q` of radius `nr`. If the M.I. of `Q` about its axis is four times that of `P` about its axis (assuming the wire to be of diameter much smaller than either radius), the value of n is
View SolutionA disc of radius 2 m and mass 100kg rolls on a horizontal floor, its centre of mass has speed of `20 cm//s`. How much work is needed to stop it ?
View SolutionThree particles, each of mass `m` grams situated at the vertices of an equilateral triangle `AbC` of side `I` cm (as shown in the figure). The moment of inertia of the system about a line `AX` perpendicular to `AB` and in the plane of `ABC`, in gram-cm^2 units will be.
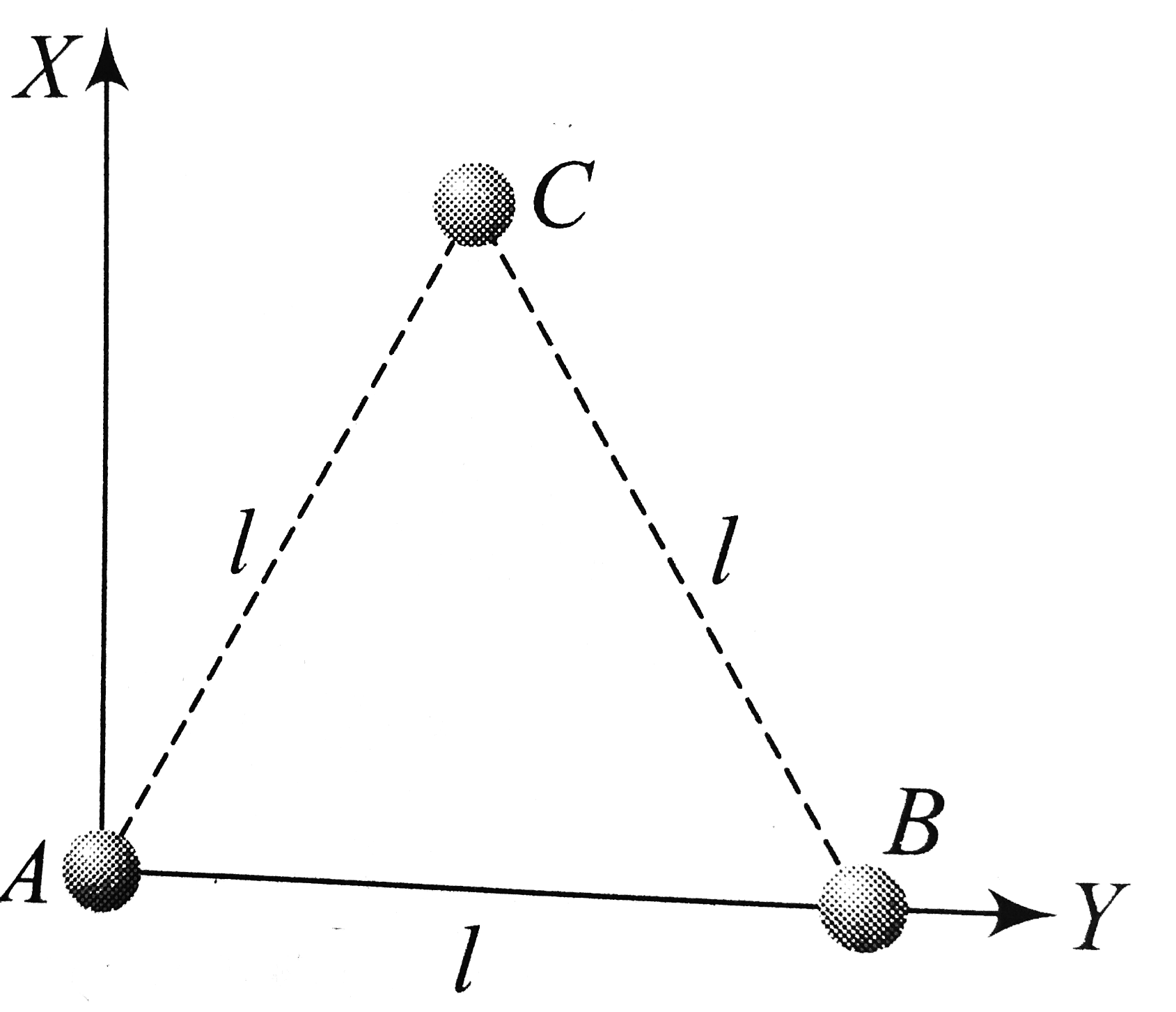 .
.
View SolutionA ladder is leaned against a smooth wall and it is allowed to slip on a frictionless floor. Which figure represents the track of its centre of mass ?
View SolutionThree identical spheres, each of mass 1 kg are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked P, Q, R respectively, the distance of centre of mass of the system from P (origin) is
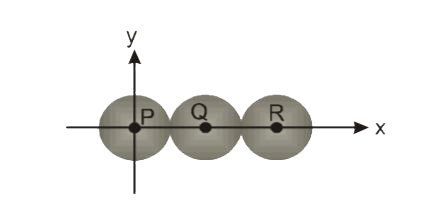
View SolutionA given shaped glass tube having uniform cross-section is filled with water and is mounted on a rotatable shaft as shown in figure. If the tube is rotated with a constant angular velocity `omega` then :

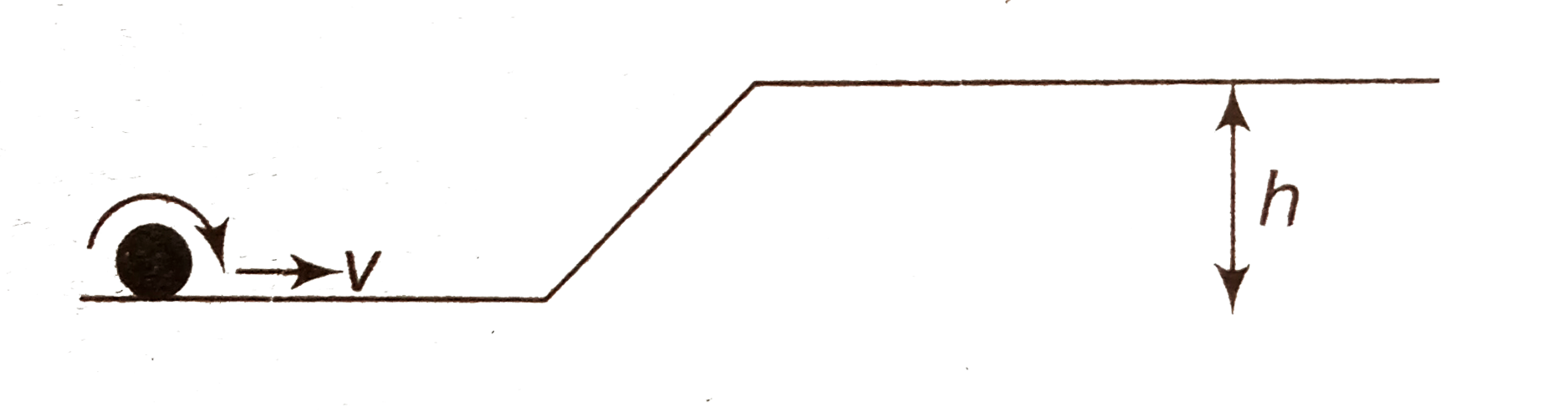
View SolutionA solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity `v m//s`. If it is to climb the inclined surface then `v` should be :
View SolutionA unifrom rod of length `l` and mass `m` is free to rotate in a vertical plane about `A`, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is `(MI "of rod about" A "is" (ml^(2))/(3))`
View SolutionA tube of length L is filled completely with an incompressible liquid of mass M and closed at both ends. The tube is then roted in a horizontal plane about one of its ends with a uniform angular velocity `omega` The force exerted by the liquid at the other end is
View SolutionThe moment of inertia of a rod about an axis through its centre and perpendicular to it, is `(1)/(12)ML^(2)` (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of `60^(@)`. The moment of inertia of the bent rod about the same axis would be
View SolutionA thin circular ring of mass `M` and radius `R` is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity `omega`. If two objects each of mass `m` be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation
`theta(t) = 2t^(3) - 6 t^(2)`
The torque on the wheel becomes zero at
View SolutionThe moment of inertia of a thin uniform rod of mass `M` and length `L` about an axis passing through its mid-point and perpendicular to its length is`I_0`. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
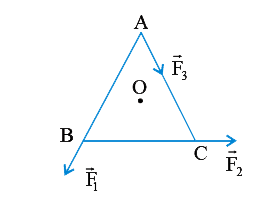
View SolutionABC is an equilateral with O as its centre `vecF_(1), vecF_(2)` and `vecF_(3)` represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of `vecF_(3)` is :
View SolutionTwo persons of masses `55 kg` and `65 kg` respectively are at the opposite ends of a boat. The length of the boat is `3.0 m` and weights `100 kg`. The `55 kg` man walks up to the `65 kg` man and sits with him. If the boat is in still water the centre of mass of the system shifts by.
View SolutionA solid cylinder of mass `50 kg` and radius `0.5 m` is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other end hanging freely. Tension in the string required to produce an angular acceleration of `2` revolution `s^(-2)` is
View SolutionThe ratio of the accelerations for a solid sphere (mass `m, and radius R`) rolling down an incline of angle `theta` without slipping, and slipping down the incline without rolling is
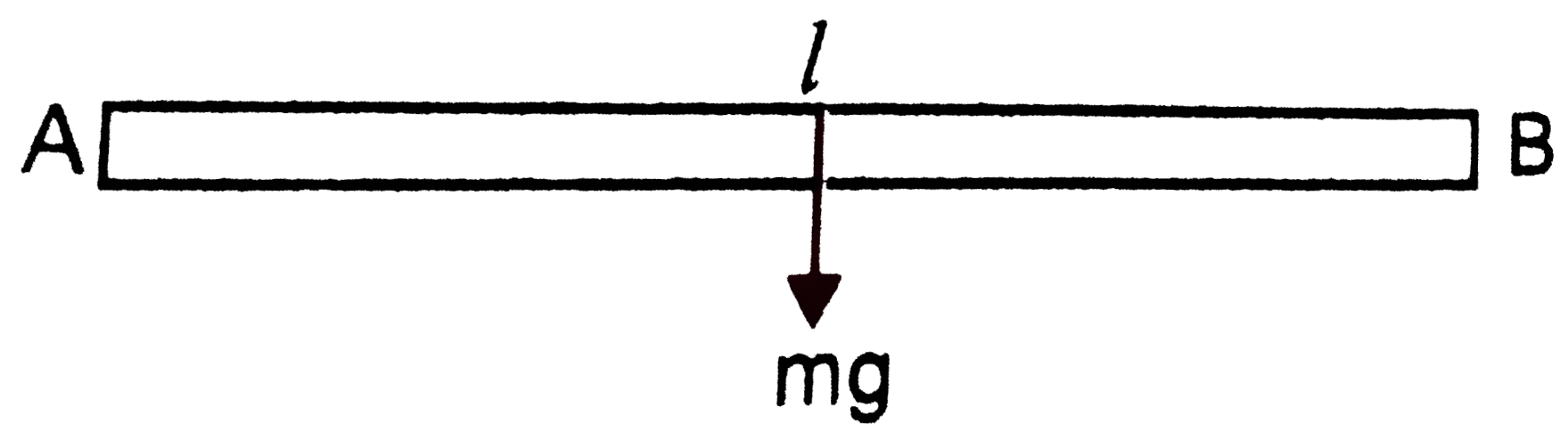
View SolutionA rod of weight `w` is supported by two parallel knife edges `A` and `B` and is in equilibrium in a horizontal position. The knives are at a distance `d` from each other. The centre of mass of the rod is at a distance `x` from `A`.
View SolutionA solid cylinder of mass 2 kg and radius 4 cm rotating about its axis at the rate of 3 rpm. The torque required to stop after `2pi` revolutions is :
View SolutionThree idential spherical shells each of mass `m` and radius `r` are placed as shown in Fig. Consider an axis XX' which is touching the two shells and passing through diameter of third shell. Moment of Inertia of the system consisting of these three spherical shells about XX' as axis is :
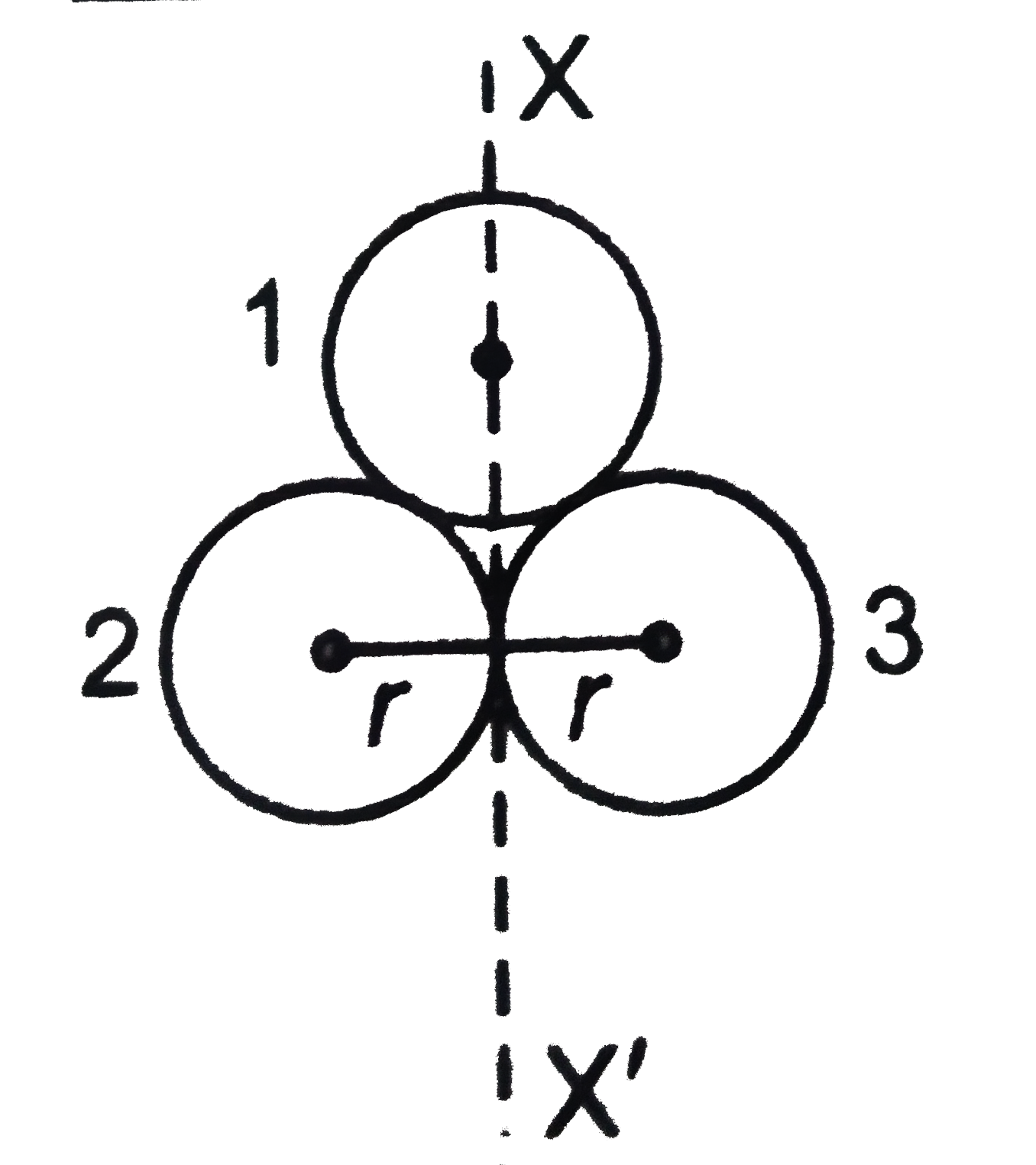
View SolutionFrom a disc of radius R and mass m, a circular hole of diamter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
View SolutionTwo discs of same moment of inertia rotating their regular axis passing through centre and perpendicular to the plane of disc with angular velocities `omega_(1)` and `omega_(2)`. They are brought into contact face to the face coinciding the axis of rotation. The expression for loss of enregy during this process is :
View Solution
COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) ) questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- Chapter Practice Test (for Board Examination)
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
- Conceptual Questions
- HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL QUESTIONS WITH ANSWERS
- NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
- NCERT FILE ( NCERT TEXTBOOK EXERCISES )
- NCERT FILE (NCERT EXEMPLAR PROBLEMS (OBJECTIVES QUESTIONS) (MULTIPLE CHOICE QUESTIONS (TYPE-I))
- NCERT FILE (NCERT EXEMPLAR PROBLEMS (SUBJECTIVES QUESTIONS) (Very Short Answer Type Questions))
- PRACTICE PROBLEMS
- PROBLEMS TOUGH & TRICKY
- REVISION EXERCISES (Additional Questions Carrying 1 mark )
- REVISION EXERCISES (Fill in the Blanks Carrying 1 mark )
- REVISION EXERCISES (Long Answer Questions Carrying 5 marks)
- REVISION EXERCISES (Numerical Problems)
- REVISION EXERCISES (Short Answer Questions Carrying 2 or 3 marks)
- REVISION EXERCISES (Very Short Answer Questions Carrying 1 mark)
- SOLVED EXAMPLES