Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not. Then
IAn>IB
IA<IB
IA=IB
IA=IB only if both the axes A and B are parallel to each other
Relation I=Icm+md2 exists only for parallel axes. So we can understand that option (d) is correct. If the two axes are not parallel then we cannot deduce any relation between them.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
Explore 48 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
Explore 35 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:REVISION EXERCISES (Numerical Problems)
Explore 20 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
In the figure shown, a planer body is in the shape of a rhombus ABCD: I1 and I2 are moment of inertias: about axis passing through centre and perpendicular to sides BC and DC respectively. I3 and I4 are amount of inertias about diagonal axis BD and AC respectively. Then the moment of inertia about an axis passing through centre and perpendicular tothe plane of body is given by

View SolutionConsider a uniform square plate shown in the figure. I1,I2,I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) I3+I4
(b) I1+I3
(c) I2+I3
(d) 12(I1+I2+I3+I4)
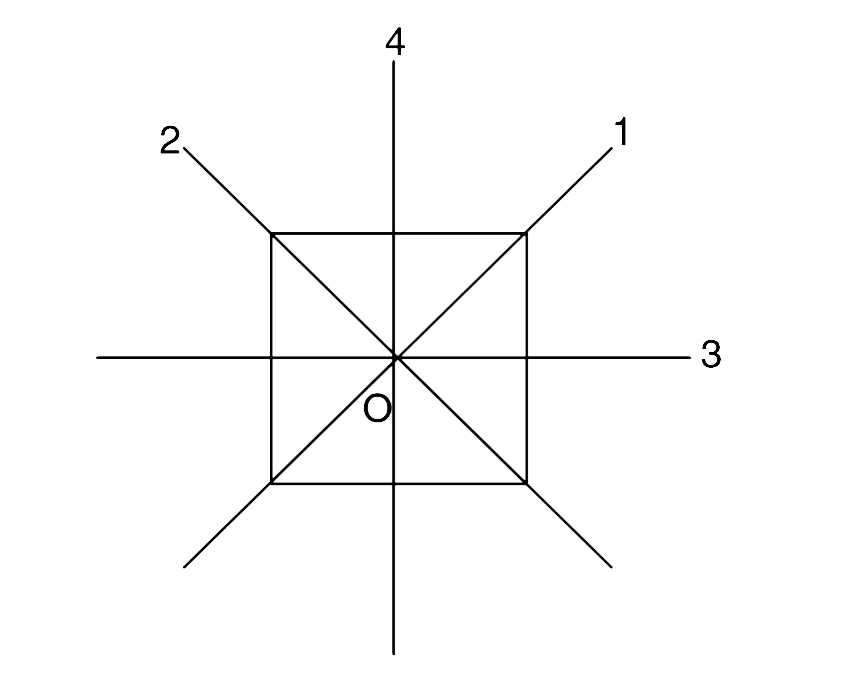
View Solution
Knowledge Check
Let IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
AIA<IBBIA<IB, whether the axes are parallel or not parallelCif the axes are parallel IA<IBDIf the axes are not parallel IA≥IBMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2Let I1 and I2 be the moment of inertia of a uniform square plate about axes APC and OPO respectively as shown in the figure.P is centre of square. The ratio I1I2 moment of inertia is -
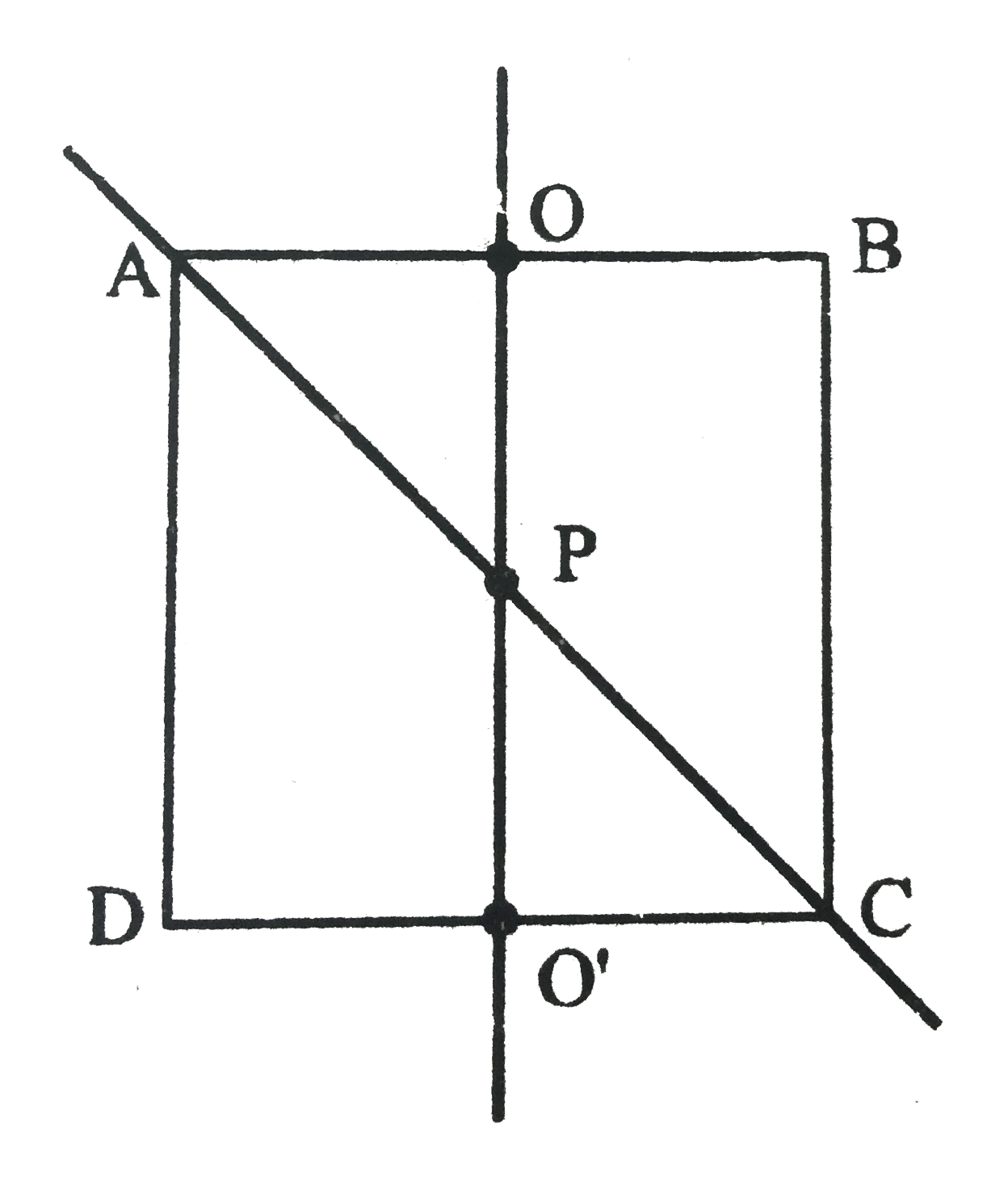 .A12√2B2C12D1
.A12√2B2C12D1
find moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown

View SolutionA semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.
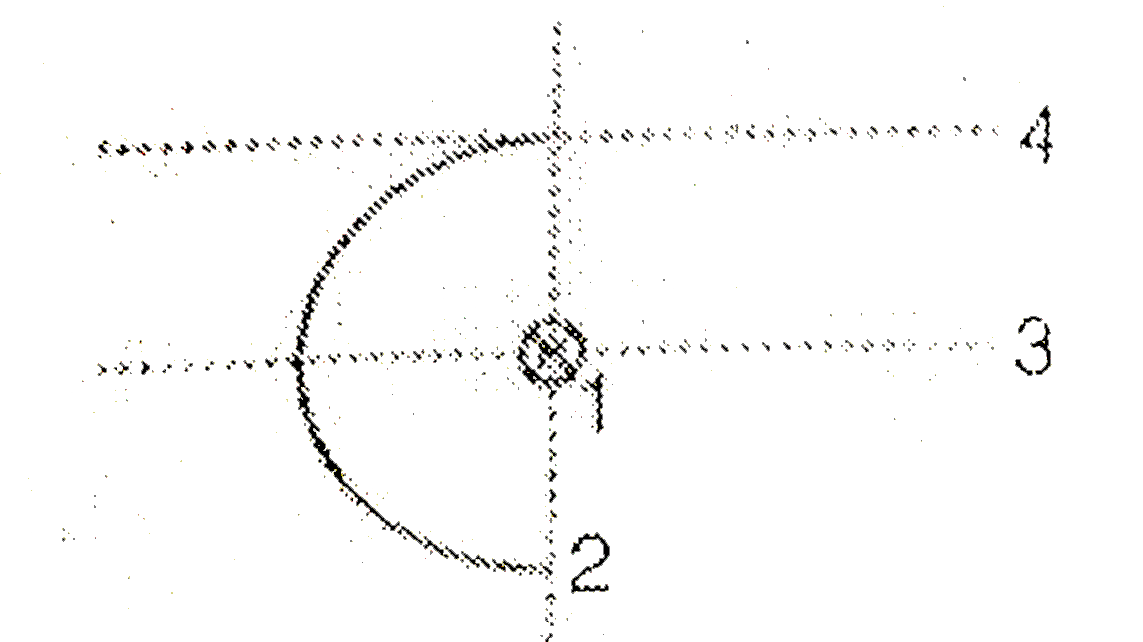

View SolutionThe moment of inertia of NaCl molecule with bond length r about an axis perpendicular to the bond and passing through the centre of mass is
View SolutionMoment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
View SolutionIn the given figure F=10N,R=1m, mass of the body is 2kg and moment of inertia of the body about an axis passing through O and perpendicular to the plane of the body is 4kgm2. O is the centre of mass of the body.

If the ground is smooth, what is the total kinetic energy of the body after 2s?
View Solution

