A ring performs pure rolling on a horizontal fixed surface with its centre moving with speed v.
Maximum possible speed that any particle of ring may have is v/√2
Minimum possible speed that any particle of ring may have is v/√2
particles on the ring may have speed anywhere between 0 and 2u.
None of these
The correct Answer is:C
We should know that in case of pure rolling on a fixed surface, point of contact remains at rest and top point moves with maximum speed which is twice the speed at the centre. Hence option (c) is correct.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )48videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )35videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - REVISION EXERCISES (Numerical Problems)20videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
In figure (a) there is a uniform cylinder of mass M and radius R. Length of the cylinder is L=√3R. The cylinder is rolling without sliding on a horizontal surface with its centre moving at speed V. In figure (b) the same cylinder is moving on a horizontal surface with its centre moving at speed V and the cylinder rotating about a vertical axis passing through its centre. [Place your pencil on the table and give a sharp blow at its end. Look at the motion of the pencil. This is how the cylinder is moving]. The angular speed is ω=VR. Write the kinetic energy of the cylinder in two cases. In which case, the kinetic energy would have been higher if length of the cylinder were doubled (=2√3R).
(a)
View SolutionA uniform ring of mass m and radius R is performing pure rolling motion on a horizontal surface. The velocity of centre of the ring is V0. If at the given instant the kinetic energy of the semi circular are AOB is lambda mv0_(2), then find the value of 11λ(takeπ=227)
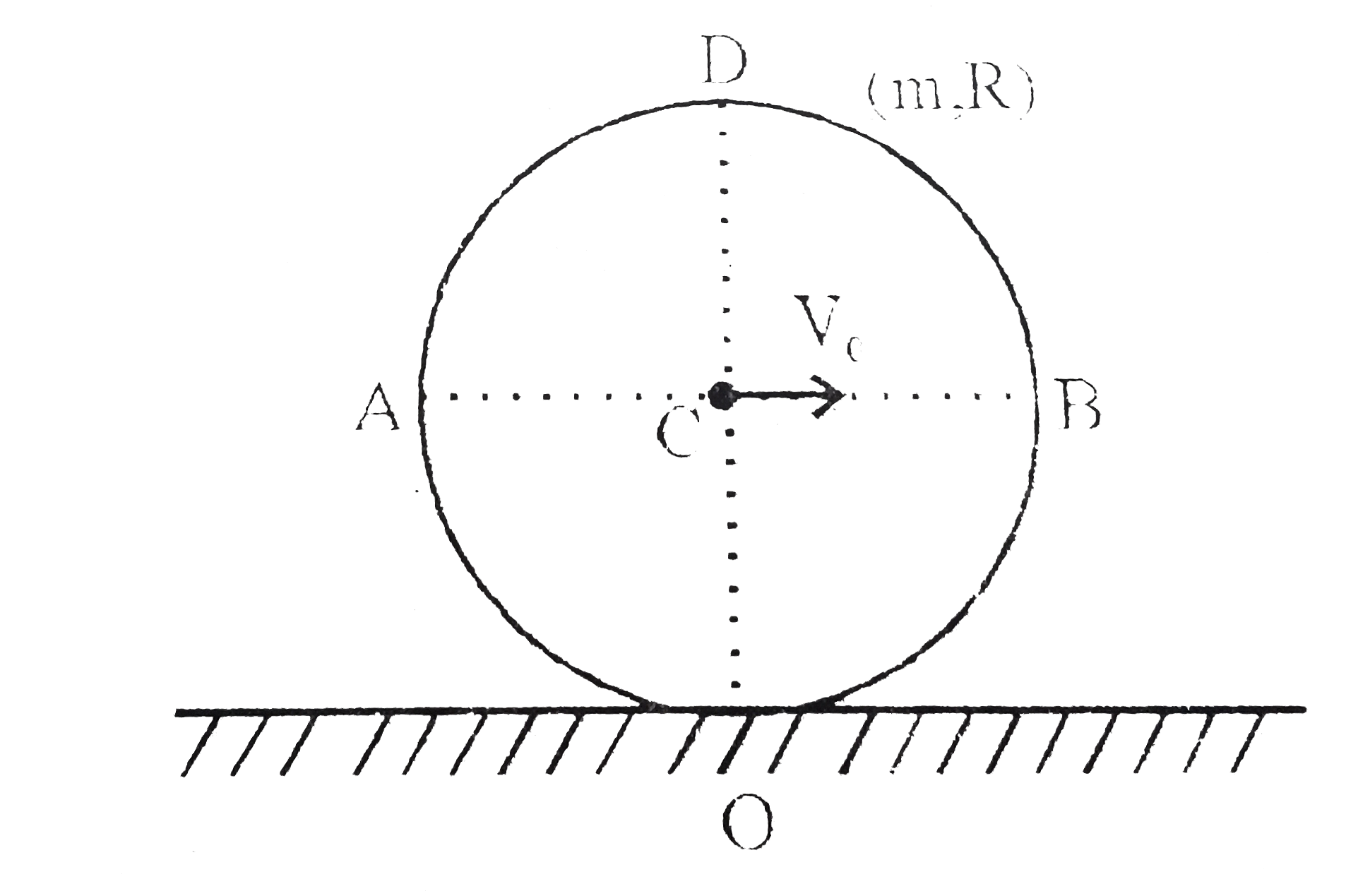
View Solution
Knowledge Check
- Question 1 - Select One
A uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
A4.17×10−4JB8.72×10−3JC6.25×10−4JD3.61×10−4J - Question 2 - Select One or More
A ring performs pure rolling on a horizontal surface and its state at some instant of time is shown in figure.
AK.E. stored in the portion AB is same as K.E. stored in the portion CDBK.E. stored in the portion AB is same as KE. stored in the portion BCCK.E. stored in the portion ABC is same as K.E. stored in the portion CDADK.E. stored in the portion ABC is less than K.E. stored in the portion CDA - Question 3 - Select One
A uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
A4×10−3JB8×10−3JC3.33×10−3JD3.5×10−3J
A cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
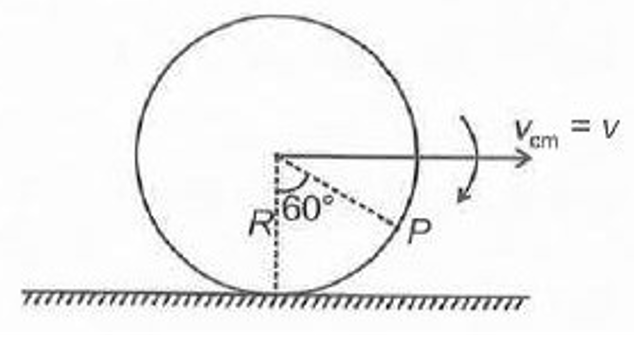
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA uniform ring rolls on a horizontal surface with out slipping. Its centre of mass moves with a constant speed v. then speed of the upper most point on its rim above the ground is
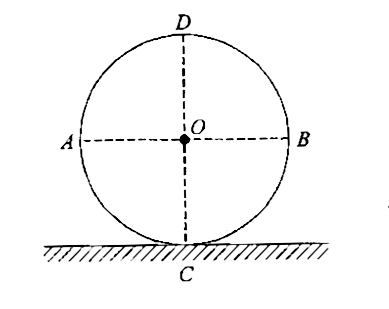
View SolutionA uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
View SolutionA sphere is performing pure rolling on a rough horizontal surface with constant angular velocity. Frictional force acting on the sphere is zero.
Velocity of contact point is zero.View Solution