A uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V0. The kinetic energy of the segment ABC is:
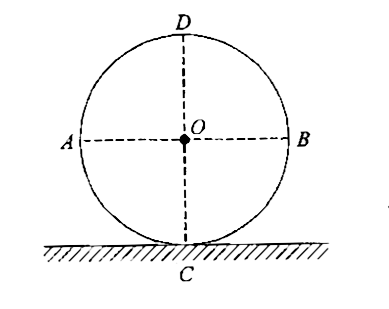
mV202−mV20π
mv202+mv20π
mv202
mv20
The correct Answer is:A
Step by step video, text & image solution for A uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is V_(0). The kinetic energy of the segment ABC is: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:MCQ
Explore 16 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Numerical MCQs Single Option Corrrect
Explore 39 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:unsolved
Explore 1 Video
Similar Questions
A uniform ring of mass m and radius R is performing pure rolling motion on a horizontal surface. The velocity of centre of the ring is V0. If at the given instant the kinetic energy of the semi circular are AOB is lambda mv0_(2), then find the value of 11λ(takeπ=227)
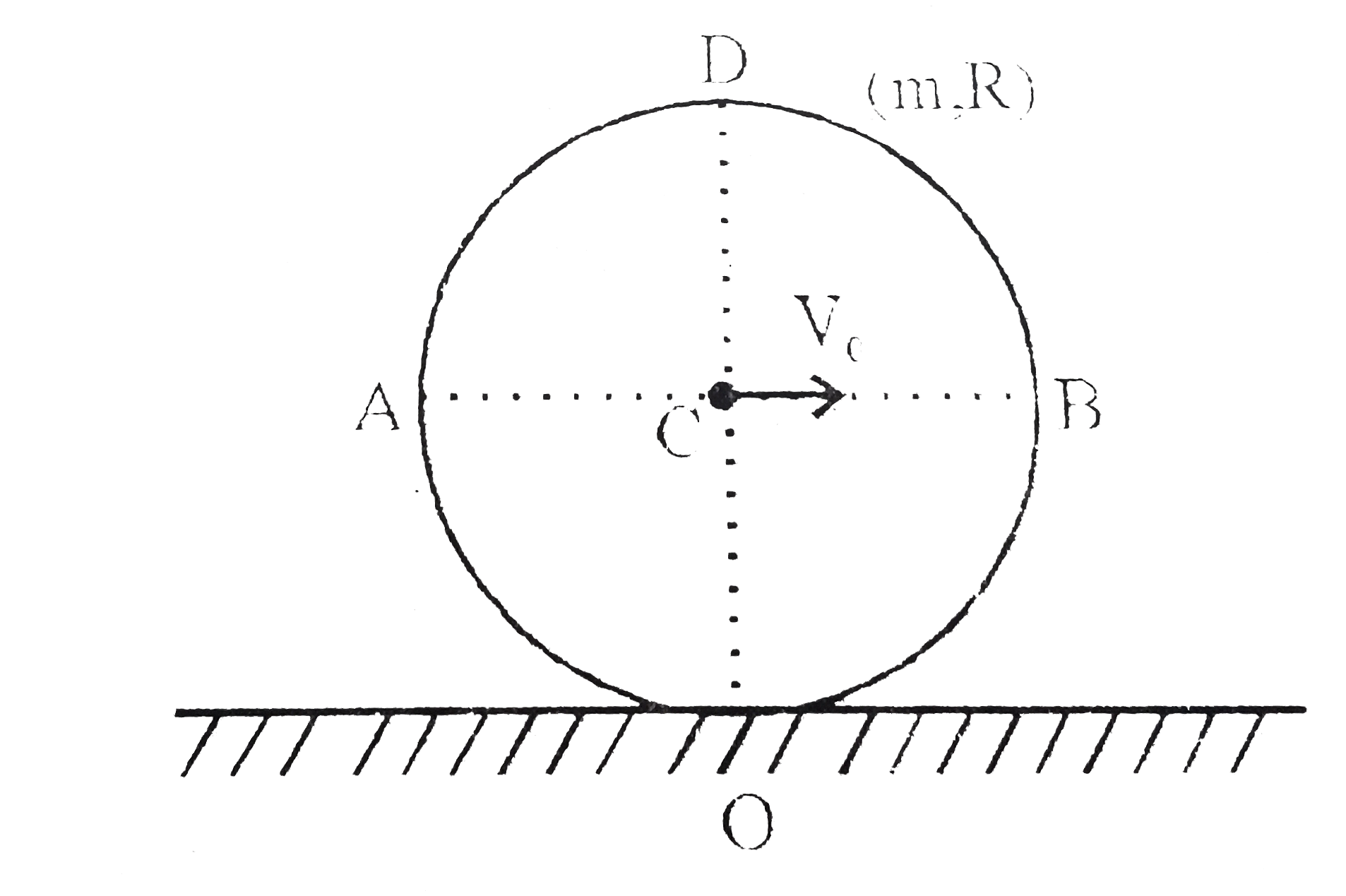
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View Solution
Knowledge Check
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMRA ring performs pure rolling on a horizontal fixed surface with its centre moving with speed v.
AMaximum possible speed that any particle of ring may have is v/√2BMinimum possible speed that any particle of ring may have is v/√2Cparticles on the ring may have speed anywhere between 0 and 2u.DNone of theseA uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
AV02BV04C3V04D0
A uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : the centre of mass
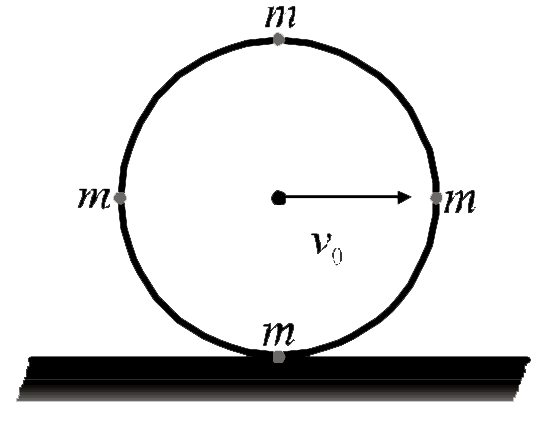
View SolutionA ring of mass m and radius R has four particles each of mass m attached to the ring as shown in figure. The centre of ring has a speed v0. The kinetic energy of the system is
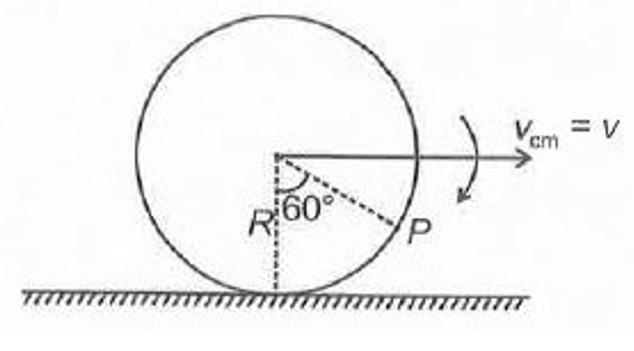
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
View SolutionA uniform circular disc of radius R is rolling on a horizontal surface. Determine the tangential velocity : at the upper most point
View SolutionA uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View Solution

