A particle is projected horizontally with velocityV0=√2ga along the smooth inside surface of a fixed hollow hemisphere of inner radius 'a' at the level of the centre 'O'. The subsequent motion of the particle is confined between the horizontal planes one through the centre and the other at a depth h. Find the value of h:
√32a
√3−13a
√5−12a
√52a
The correct Answer is:C
Step by step video, text & image solution for A particle is projected horizontally with velocityV_(0)=sqrt(2ga) along the smooth inside surface of a fixed hollow hemisphere of inner radius 'a' at the level of the centre 'O'. The subsequent motion of the particle is confined between the horizontal planes one through the centre and the other at a depth h. Find the value of h: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:MCQ
Explore 16 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Unsolved Numerical
Explore 63 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:Numerical MCQs Single Option Corrrect
Explore 39 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:unsolved
Explore 1 Video
Similar Questions
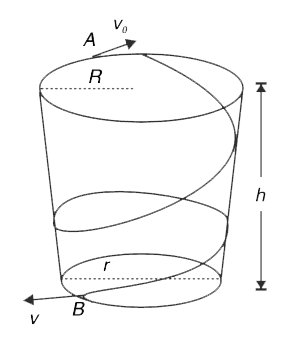
A frustum has been mounted with its axis vertical. It has a height h and radii of its upper and lower cross sections are R and r respectively. A particle is projected with horizontal velocity v0 along its upper brim. The particle spirals down the inner surface and leaves the lower face at point B. The inner wall of the frustum is smooth.
(a) Find the vertical component of velocity of the particle as it leaves the frustum at B.
(b) Find minimum value of h for which the particle will never come out of the frustum.
Take r=R2 for solving this part of the problem.
View SolutionA small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemispherical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the vertical centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.

View Solution
Knowledge Check

A hollow sphere of mass m and radius R is placed on smooth gound. A particle of mass m is projected with velocity v0 and angle θ lowest point a inside the sphere as shown in diagram if particle strikes the sphere at a point which is on horizontal level of centre and at that moment particle is at highest point. The collision between particle and sphere is elastic. The value of v0 isAv0=√RgcosθBv0=√2RgsinθC2√RgtanθDv0=√Rg2[1+cos2θ]In a cylinderical region uniform magnetic field is present as shown in the figure. The cylinder is kept on a horizontal plane and its axis is horizontal. If a charge particle of mass m and charge q is projected horizontally with velocity v through a hole normal to the axis of the cylinder as shown in the diagram. An observer states the particle moves first undeviated and subsequently. oscillates inside cylinder along a horizontal diameter passing through axis of the cylinder time period
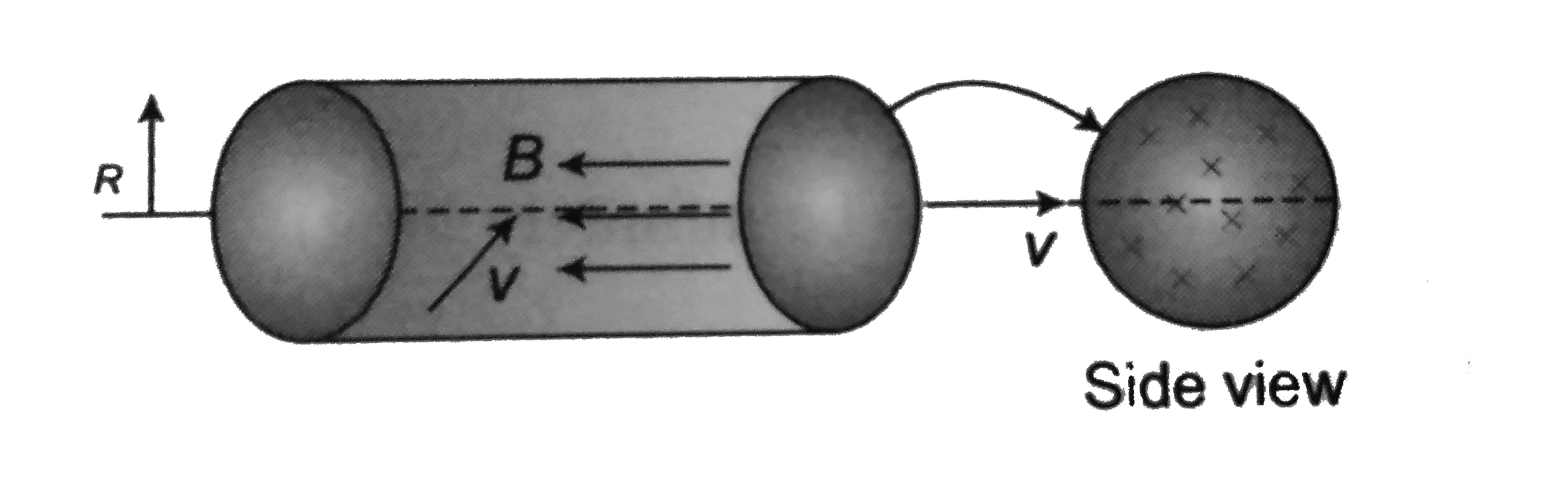 Aoscillates inside cylinder along a horizontal diameter passing through axis of the cylinder time period 4RqBmgBoscillates inside cylinder along a horizontal diameter passing through axis of the cylinder time period 2qRBmgCoscillates inside cylinder along a horizontal diameter passing through axis of the cylinder time period mgqBRDIt is not possible for the particle to oscillates in this given situation
Aoscillates inside cylinder along a horizontal diameter passing through axis of the cylinder time period 4RqBmgBoscillates inside cylinder along a horizontal diameter passing through axis of the cylinder time period 2qRBmgCoscillates inside cylinder along a horizontal diameter passing through axis of the cylinder time period mgqBRDIt is not possible for the particle to oscillates in this given situationA particle is describing circular motion in a horizontal plane in contact with the smooth surface of a fixed rigid circular cone with its axis vertical and vertex down. The height of the plane of motion above the vertex is h and the semi-vertical angle of the cone is α The period of revolution of the particle
 Aincreases as h increasesBdecreases as h decreasesCincreases as α increasesDdecreases as α decreases
Aincreases as h increasesBdecreases as h decreasesCincreases as α increasesDdecreases as α decreases
A particle slides down from the top outside smooth surface of a fixed sphere of radius a=10m . The initial horizontal velocity to be imparted to the particle at the top is 5Km/s ,if it leaves the surface at a point whose vertical height above the centre of sphere is 3a/4. Find the value of K
View SolutionParticle slides down the surface of a smooth fixed sphere of radius r starting from rest at the highest point. Find where it will leave the sphere. Show that it strike the horizontal plane through the lowest point of the sphere at a distance equal to 5[√5+4√2](r/27) from the vertical diameter.
View SolutionA small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
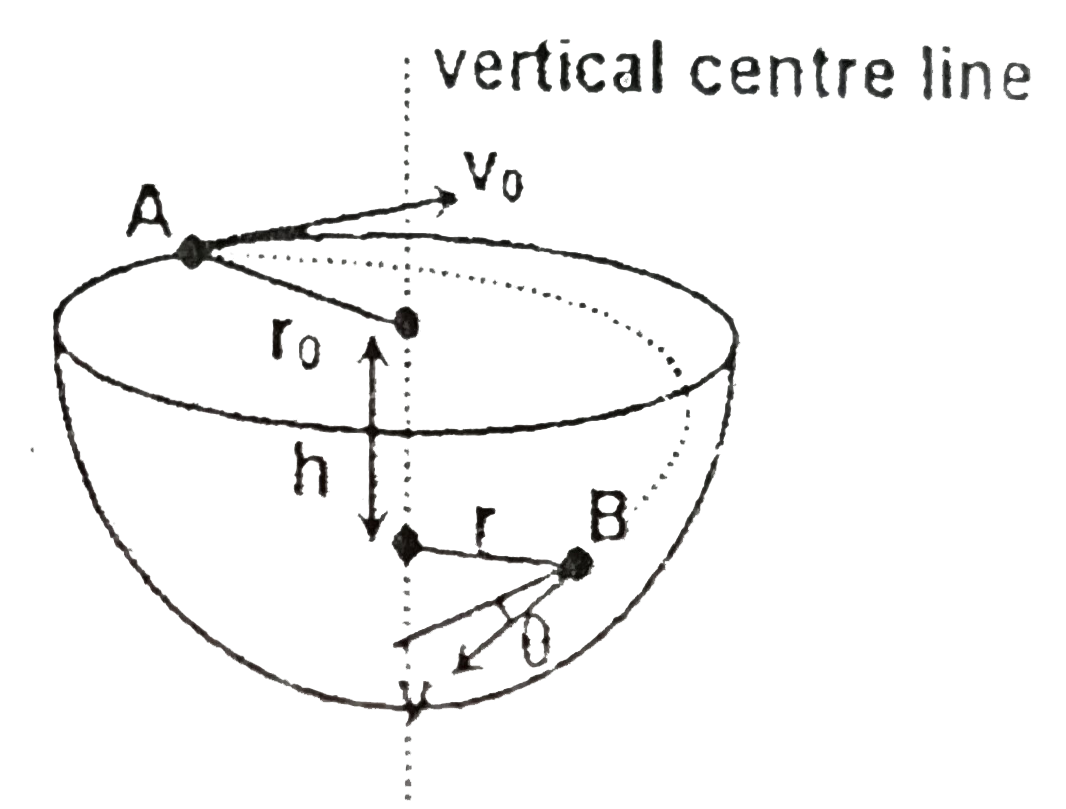
View SolutionA small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)

View SolutionA particle of mass m and velocity v0 is fired at a solid cylinder of mass M and radius R. The cylinder is initially at rest and is mounted on a fixed horizontal axle that runs through the centre of mass. The line of motion of the particle is perpendicular to the axle and at a distance d, less than R, from the centre and the particle sticks to the surface of hte cylinder, then
View Solution

