Complete Solutions to SOLVED EXAMPLES of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| MODERN PUBLICATION | SOLVED EXAMPLES |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
The distance between the centres of carbon and oxygen atoms in the carbon monoxide molecule is `1.130Å` . Locate the centre of mass of the molecule relative to the carbon atom .
View SolutionIf three point masses `m_(1),m_(2) and m_(3)` are situated at the vertices of an equilateral triangle of side a, then what will be the co-ordinates of the centre of mass of this system ?
View SolutionPosition vector of two particles of masses 200 g and 400 g at a given time are `3hati+hatj+9hatk ` m and `-2hati+6hatj-hatk`, respectively. Find the instantaneous position of the centre of mass of the system.
View SolutionFind the centre of mass of a uniform `L` shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is `3kg`.

View SolutionLocate the position of the centre of mass of a hemisphere of radius R as shown in the following figure:
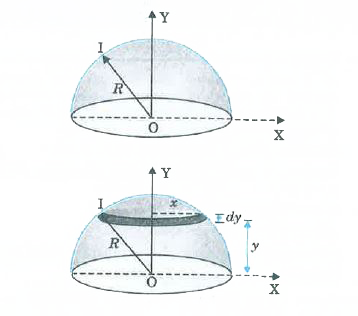
View SolutionThe instantaneous velocities of two particles of masses 200 g and 400 g at a given time are `12hati-7hatj-5hatk` m/s and `8hati-9hatj-5hatk` m/s, respectively. Calculate the instantaneous velocity of the centre of mass of the system.
View SolutionA wheel is turned from rest through 500 radians in 20 s by applying a constant torque.
(a) Calculate the angular acceleration of wheel
(b) ind the angular velocity of the wheel after 40s from start if its angular acceleration is same.
View SolutionA wheel of a bicycle is rotating about its axis with an angular velocity of 100 rpm. When the brakes are applied, the wheel comes to rest in 10 s. Calculate the number of revolutions made by the wheel before coming to rest. Assume that the deceleration is constant.
View SolutionA car moves on a road with a speed of `54 km h^(-1)`. The radius of its wheels is `0.35 m`. What is the average negative torque transmitted by its brakes to the wheels if the car is brought to rest in `15 s`? Moment of inertia of the wheels about the axis of rotation is `3 kg m^(2)`.
View SolutionA cylinder of length 10 cm and radius 5 cm is rotating with an angular speed of 50 rad/s about its central axis. Calculate the uniform tangential force which will stop the cylinder in 8 s. The moment of inertia of the cylinder about its axis of rotation is `0.6 kg m^(2)`.
View SolutionA cord of negligible mass is wound around the rim of a wheel of radius 20 cm. An object of mass 600 g is attached to the end of the cord and is allowed to fall from rest. It took 5 s for the object to fall by 2 m. Calculate the angular acceleration and moment of inertia of the wheel. Assume that the axis of wheel is horizontal.
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass `20 kg` and radius `20 cm`. A steady pull of `25 N` is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
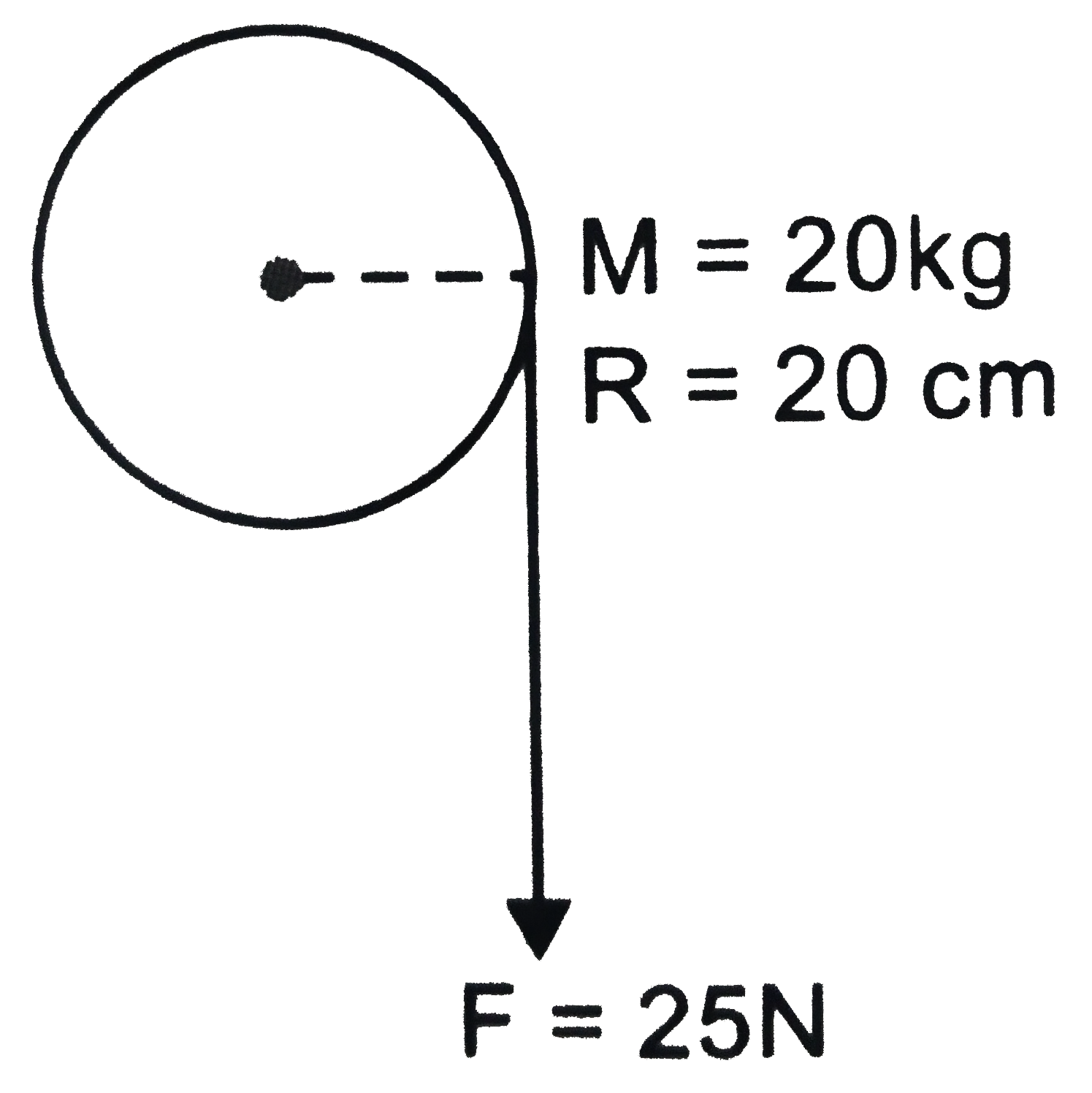
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when `2 m` of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionCalculate the moment of inertia of an oxygen molecule about an axis passing through its centre of mass and perpendicular to the internuclear axis. Take
Mass of O-atom `=2.67xx10^(-26)kg`
Interatiomic distance `=1.2xx10^(-10)m`
View SolutionThree particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
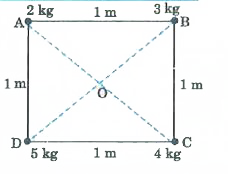
View SolutionFour point masses 2 kg, 3 kg, 4 kg and 5 kg are respectively located at the four corners A, B, C and D of a square of side 1 m as shown in the following figure. Calculate the moment of inertia of the system about
(i) an aris coinciding with side BC
(ii) an axis coinciding with diagonal BD
(iii) an axis passing through A and perpendicular to the plane of the square.
View SolutionFor a uniform circular disc the moment of inertia about its diameter is `150gcm^(2)`. Calculate its moment of inertia about
(i) its tangent parallel to diameter.
(ii) an axis perpendicular to its plane and passing through centre.
View SolutionCalculate the moment of inertia of a circular disc of radius 8 cm, thickness 2 mm and uniform density `10gcm^(-3)`, about a transverse axis passing through its centre.
View SolutionFour spheres of diameter a and mass m each are arranged at the corners of a square of side 1. Calculate the moment of inertia of the system about CD taken as its axis.
View SolutionA rectangular bar magnet of mass 100 g has length, breadth and thickness of 10 cm, 4 cm and 2 cm, respectively. Calculate its moment of inertia about an axis passing through its centre and parallel to its thickness.
View SolutionThe radius of a sphere is 8 cm. What will be its radius of gyration about (i) its diameter and (ii) about any tangent?
View SolutionCalculate the moment of inertia of a body about its axis of rotation if its angular momentum is 62.8 Js and it has 10 revolutions per second.
View SolutionCalculate the angular momentum of earth rotating about its own axis. Take
Radius of earth `=6.4xx10^(6)m`
Mass of earth `=5.97xx10^(24)kg`
View SolutionA wheel of mass 2 kg and radius 20 cm initially at rest is free to rotate about its axis. It receives an angular impulse of `4kgm^(2)s^(-1)` initially and similar impulse after every 5 s of initial one. Calculate the angular speed of the wheel 22 s after the initial impulse.
View SolutionCalculate the angular momentum of a bike of mass 500 kg moving in a circular track of radius 20 m with a speed of 30 m/s.
View SolutionA satellite of mass `M_(s)` is revolving around the earth (Mass M) in a orbit of radius R. Find its angular momentum.
View SolutionAn ice skater has her arms outstretched and is spinning with a rate of 2 rotations per second. Her moment of inertia at this instant is `1.48kgm^(2)`. She then pulls her arms inside to increase her rate of spin and her moment of inertia becomes `0.56kgm^(2)`. Calculate her new rate of rotation.
View SolutionImagine that the earth suddenly contracts to one-third of its present radius, without any external torque on it. By what duration the day on the earth will decrease considering the earth to be a perfect solid sphere.
View SolutionThe sun rotates about its axis once in 27 days. If it suddenly shrinks to one-eighth of its original volume, mass remaining same, then what will be its new period of rotation?
View SolutionA uniform disc is rotating freely about a vertical axis passing through its centre and makes 100 rpm. A small piece of gum of mass 8 g falls vertically on the disc and sticks to it at a distance of 5 cm from its axis. If the number of rotations per minute reduces to 80 rpm find the moment of inertia of the disc.
View SolutionDetermine the moment of inertia of a wheel rotating at a rate of 1200 rpm about its axis of rotation. Given that the kinetic energy of the wheel is `3xx10^(6)J`.
View SolutionTo increase the speed of a flywheel from 60 rpm to 360 rpm, energy of 490 J is spent. Calculate the moment of inertia of wheel.
View SolutionA rod of length 2 m is held vertically with one of its end on the floor. It is then allowed to fall. Calculate the speed of the other end when it strikes the floor. Assume that the end of the rod which is on the floor does not slip.
View SolutionA solid sphere of mass 10 kg and radius 0.5 m is rolling on a road without sliding with an regular velocity of 12 rad/s. What is the percentage of rotational kinetic energy in the total kinetic energy of the wheel?
View SolutionA solid cylinder of mass 8 kg is rolling perfectly down an inclined plane of inclination 30. Calculate the force of friction between the cylinder and inclined plane and acceleration of the cylinder down the inclined plane.
View SolutionThree bodies, a ring, a soild cylinder and a soild sphere roll down the same inclined plane without slipping. They start from rest. The radii of the bodies are identical. Which of the bodies reaches the ground with maximum velocity ?
View SolutionA solid cylinder of mass 500 g and radius 10 cm rolls down an inclined plane of inclination 1 in 10. Calculate its acceleration and total energy after 6 s.
View SolutionA metal bar `70 cm` long and `4.00 kg` in mass is supported on two knife edges placed `10 cm` from each end. A `6.00 kg` weight is suspended at `30 cm` from one end. Find the reactions at the knife edges. Assume the bar to be of uniform cross-section and homogeneous.
View SolutionA 3 m long ladder weighing 20 kg leans on a frictionless wall. Its feet rest on the floor 1 m from the wall as shown in the following figure, Find the reaction forces of the wall and the floor.
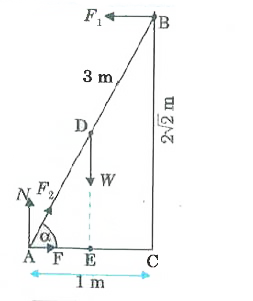
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- Chapter Practice Test (for Board Examination)
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
- Conceptual Questions
- HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL QUESTIONS WITH ANSWERS
- NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
- NCERT FILE ( NCERT TEXTBOOK EXERCISES )
- NCERT FILE (NCERT EXEMPLAR PROBLEMS (OBJECTIVES QUESTIONS) (MULTIPLE CHOICE QUESTIONS (TYPE-I))
- NCERT FILE (NCERT EXEMPLAR PROBLEMS (SUBJECTIVES QUESTIONS) (Very Short Answer Type Questions))
- PRACTICE PROBLEMS
- PROBLEMS TOUGH & TRICKY
- REVISION EXERCISES (Additional Questions Carrying 1 mark )
- REVISION EXERCISES (Fill in the Blanks Carrying 1 mark )
- REVISION EXERCISES (Long Answer Questions Carrying 5 marks)
- REVISION EXERCISES (Numerical Problems)
- REVISION EXERCISES (Short Answer Questions Carrying 2 or 3 marks)
- REVISION EXERCISES (Very Short Answer Questions Carrying 1 mark)
- SOLVED EXAMPLES