Complete Solutions to COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS) ) of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| MODERN PUBLICATION | COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS) ) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
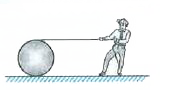
String is wrapped on a cylinder and free end of the string is pulled by a man as shown in figure. Horizontal surface is sufficiently rough. Person pulls `l_(1)` length of string and centre of the cylinder is found to move by a distance `l_2`. Calculate `l_(1)//l_(2)`.
View SolutionA hollow cylinder of mass m and radius r is kept on a smooth horizontal surface. Horizontal force F is applied at a height above the centre. Find the value of h/R so that ring performs pure rolling on the surface.
View SolutionA very small solid sphere is set rolling on a rough horizontal track which becomes circular after certain distance. Radius of the circular portion of the track is R which is large compared to radius r of the sphere. Ifaim is that sphere should complete the circle successfully then minimum required speed at the bottom is found to be `sqrt((27gR)/(n))` Calculate .
View SolutionA solid sphere is rolling on a horizontal surface such that speed of the centre of sphere is u. Mase of the sphere is m and radius R. Magnitude of angular momentum about the point of contact is found to be `(7)/(n)mvR`/. Find the value of n
View SolutionA ring is set to rotate with angular speed `omega_(0)` in gravity-free space. Ring is made from flexible material and due to centrifugal action its radius starts increasing slowly. After some time radius of ring becomes twice of its initial value and its angular velocity is found to be `omega` . Calculate `omega_(0)// omega`.
View SolutionAtube is completely filled with some incompressible liquid having total mass m. Length of the tube is L. Tube is rotated in horizontal plane, about one of its ends and force exerted by the tube on liquid on the other end is found to be `(1)/(n)m L omega^(2)`. Here `omega` is uniform angular velocity of tube. Calculate the value of n.
View SolutionMoment of inertia of the rod about an axis passing through the end and perpendicular to the length of the rod is `I_(0)`. If axis of rotation is inclined at an angle `30^(@)` with the length then moment of inertia is found to be `I`. Calculate value of `I_(0)//I`
View SolutionA ring and a disc are initially at rest, side by side, at the top of an inclined plane which makes an angle `60^(@)` with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is `(2 - sqrt(3)) //sqrt(10s)` 2– 3 / 10s, then the height of the top of the inclined plane, in metres, is _____________ . Take `g = 10ms^(-2)`
View SolutionA solid sphere is released from the state of rest on an inclined plane. Mass of the sphere is m and its radius is r. Inclined plane makes an angle with the horizontal. If minimum coefficient of friction required for pure rolling is `(n)/(7)tan theta` then calculate value of n.
View SolutionA particle of mass m is moving perpendicular to a rod of length L kept on a frictionless horizontal surface and collides at a distance L/4 from the centre of rod. Particle comes to state of rest just after collision. Mass of rod is M and speed of particle before collision is u. Let v is the velocity of centre of rod after collision and is angular velocity attained by the rod. Find `(Lomega)/(v)`
View SolutionA binary star consists of two stars `A(mass 2.2 M_s)` and B `(mass 11 M_s)` where `M_s` is the mass of the sun, they are separted by distane d and are rotating about their center of mass, which is stationary. The ratio of the total angular momentum of the binary to the angular momentum of star B about the centre of mass is
View SolutionA uniform circular disc of mass 50kg and radius 0.4 m is rotating with an angular velocity of `10 rad s^(-1)` about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m, are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity `(in red s^(-1))` of the system is
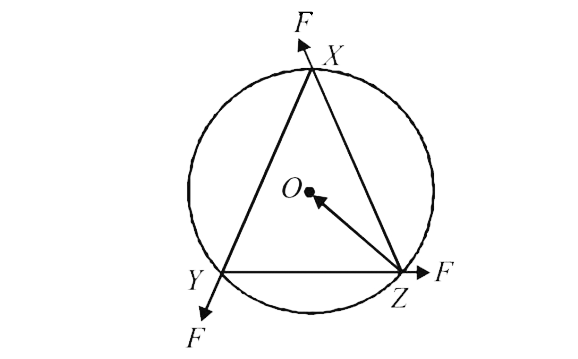
View SolutionA uniform circular disc of mass 1.5 kg and raius 0.5 m is initially ar rest on a horiozntal frictonless surface. Three forces of equal matgnitude F = 0.5 N are applied simultaneously along the three sides of an equilateral triangle XYZ with its vertices on the perimeter of the disc (see figure). One second after applying the forces the angular speed of the disc in `rad s^(-1)` is
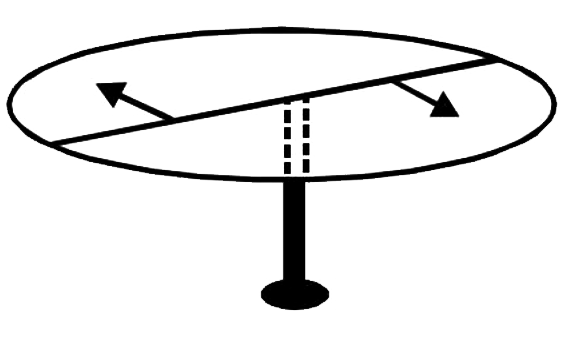
View SolutionA horizontal circular platform of radius 0.5 m and mass axis. Two massless spring toy-guns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of `9ms^(-1)` with respect to the ground. The rotational speed of the platform in `rad s^(-1)` after the balls leace the platform is
View SolutionThe densitis of two solid spheres A and B of the same radii R very with radial distance `r as p_A(r ) = k ((r )/(R )) and p_B(r ) = k((r )/(R )^5,` respectively, where k is a constant . The moments of inertia of the inividual spheres about axes passing throgh their centres are `I_A and I_B` respectively. if `(I_B)/(I_A) = (n)/(10),` the value of n is
View Solution
COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS) ) questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of MODERN PUBLISHERS PHYSICS (HINGLISH) of Class 11
All Exercises from MODERN PUBLICATION Class 11 PHYSICS SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- Chapter Practice Test (for Board Examination)
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
- COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )
- COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )
- Conceptual Questions
- HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL QUESTIONS WITH ANSWERS
- NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
- NCERT FILE ( NCERT TEXTBOOK EXERCISES )
- NCERT FILE (NCERT EXEMPLAR PROBLEMS (OBJECTIVES QUESTIONS) (MULTIPLE CHOICE QUESTIONS (TYPE-I))
- NCERT FILE (NCERT EXEMPLAR PROBLEMS (SUBJECTIVES QUESTIONS) (Very Short Answer Type Questions))
- PRACTICE PROBLEMS
- PROBLEMS TOUGH & TRICKY
- REVISION EXERCISES (Additional Questions Carrying 1 mark )
- REVISION EXERCISES (Fill in the Blanks Carrying 1 mark )
- REVISION EXERCISES (Long Answer Questions Carrying 5 marks)
- REVISION EXERCISES (Numerical Problems)
- REVISION EXERCISES (Short Answer Questions Carrying 2 or 3 marks)
- REVISION EXERCISES (Very Short Answer Questions Carrying 1 mark)
- SOLVED EXAMPLES