Question

The densitis of two solid spheres A and B of the same radii R very with radial distance $ras{p}_A\left(r\right)=k\left(\frac{r}{R}\right)\text{and}{p}_B\left(r\right)=k(\frac{r}{{\left(R\right)}^5},$ respectively, where k is a constant . The moments of inertia of the inividual spheres about axes passing throgh their centres are $I_A\text{and}{I}_B$ respectively. if $\frac{I_B}{I_A}=\frac{n}{10},$ the value of n is

Answer

6

Explanation

Let us select a segment in the form of a spherical shell of radius x and radial thickness dx.

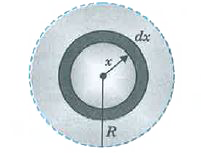
Moment of inertia of this spherical segment can be written as follows:
`(dI)=(2)/(3)(dm)x^(2)`
`impliesdI=(2)/(3)(4pix^(2)dxxxrho(x))x^(2)=(8)/(3)pix^(4)rho(x)dx`
`impliesI=(8)/(3)piint_(0)^(R)x^(4)rho(x)dx`
`(I_(B))/(I_(A))=((1)/(R^(5))int_(0)^(R)x^(4).dx)/((1)/(R)int_(0)^(R)x^(5).dx)=((1)/(10).R^(5))/((1)/(6)R^(5))=(6)/(10)`
On comparing with the given result we get n-6.