A cord of negligible mass is wound around the rim of a wheel of radius 20 cm. An object of mass 600 g is attached to the end of the cord and is allowed to fall from rest. It took 5 s for the object to fall by 2 m. Calculate the angular acceleration and moment of inertia of the wheel. Assume that the axis of wheel is horizontal.
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the acceleration of the falling object
We know that the object falls a distance of s=2m in time t=5s. We can use the second equation of motion:
s=ut+12at2
Since the object starts from rest, u=0. Thus, the equation simplifies to:
s=12at2
Substituting the known values:
2=12a(52)
2=12a(25)
2=252a
Multiplying both sides by 2:
4=25a
Now, solving for a:
a=425m/s2
Step 2: Calculate the angular acceleration of the wheel
The angular acceleration α of the wheel is related to the linear acceleration a by the formula:
a=rα
Where r is the radius of the wheel. Given that the radius r=20cm=0.2m:
425=0.2α
Now, solving for α:
α=4/250.2=425×0.2=45rad/s2
Step 3: Calculate the moment of inertia of the wheel
To find the moment of inertia I, we can use the relationship between torque τ, moment of inertia I, and angular acceleration α:
τ=Iα
The torque due to the weight of the falling object is given by:
τ=r⋅F=r⋅mg
Where m=600g=0.6kg and g=9.8m/s2. Thus:
τ=0.2⋅(0.6⋅9.8)
Calculating τ:
τ=0.2⋅5.88=1.176N m
Now substituting into the torque equation:
1.176=I⋅45
Solving for I:
I=1.17645=1.176⋅54=1.47kg m2
Final Answers:
- Angular acceleration α=0.8rad/s2
- Moment of inertia I=1.47kg m2
- Moment of inertia I=1.47kg m2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PRACTICE PROBLEMS
Explore 26 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Conceptual Questions
Explore 24 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A cord is wound around the circumference of a wheel of diameter 0.3 m. The axis of the wheel is horizontal. A mass of 0.5 kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5 m in 4s, what is the angular acceleration of the wheel ? Also find out the moment of inertia of the wheel.
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
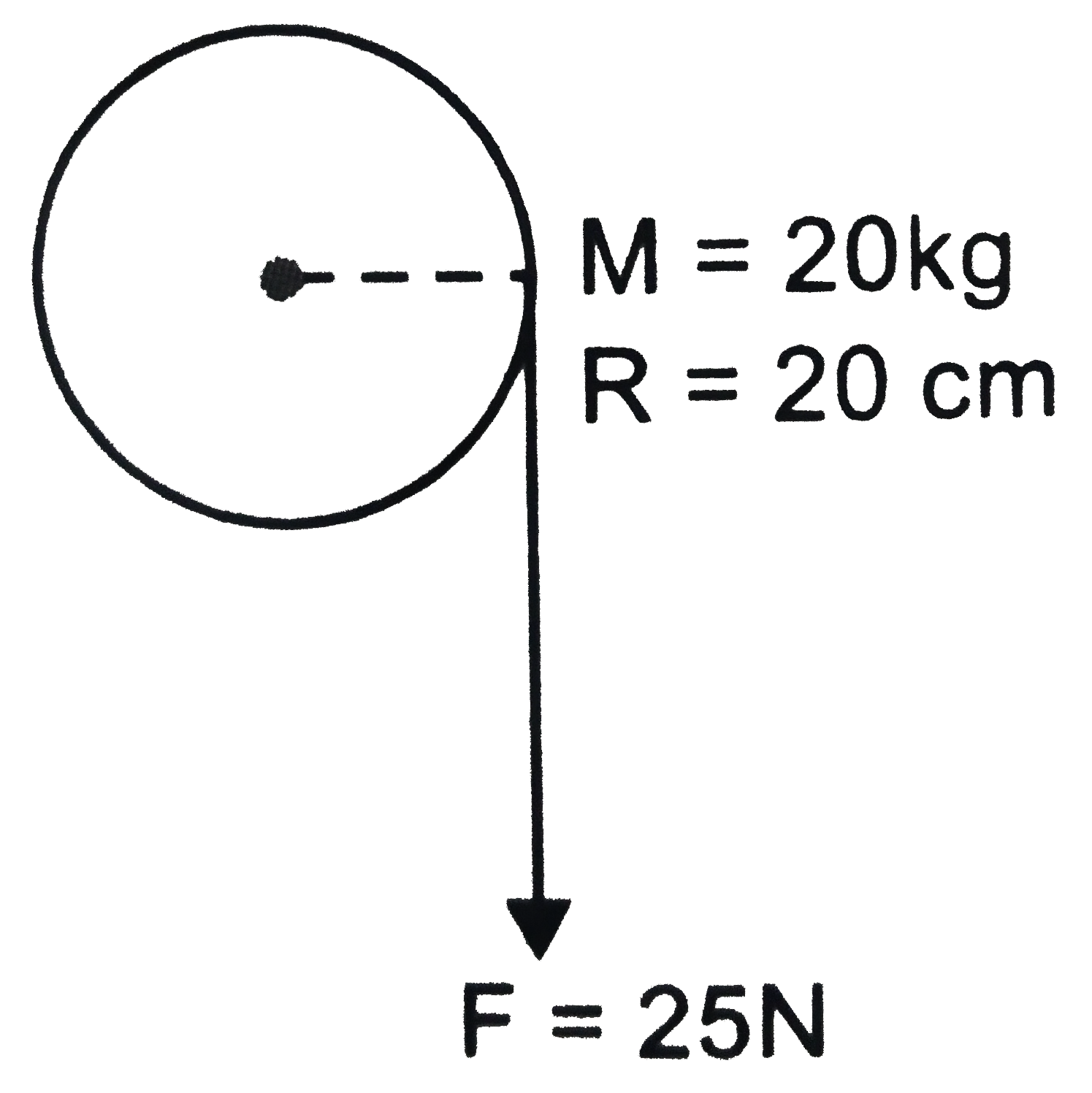
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View Solution
Knowledge Check
A cord of negligible mass is wound round the rin of a flywheel of mass 20 kg and radius 20 cm. A steady pull of 25 N is applied on the cord. The work done by the pull when 2 m of the cord is unwound is
A20 JB25 JC45 JD50 JA cord is wound over the rim of a flywheel of mass 20 kg and radius 25 cm. A mass 2.5 kg attached to the cord is allowed to fall under gravity. The angular acceleration of the flywheel is
A25rad/s2B20rad/s2C10rad/s2D5rad/s2A cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and MI is I. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
A√2ghI+mr2B(2mghI+mr2)1/2C(2mghI+2mr2)1/2D√2gh
A cord is wound around the circumference of a bicycle wheel (without tyre) of diameter 1m. A mass of 2kg is tied at the end of the cord and it is allowed to fall from rest. The weight falls 2m in 4s. The axle of the wheel is horizontal and the wheel rotates which its plane vertical. if g=10ms−2, what is the angular acceleration of the wheel ?
View SolutionA cord is wound round the circumference of a wheel of radius r. The axis of the wheel is horizontal and its moment of inertia about this axis is I. A weight mg is attached to the end of the cord and is allowed to fall from rest. The angular velocity of the wheel, when the weight has fallen through a distance h, is
View SolutionA cord is wound round the circumference of wheel of radius r. The axis of the wheel is horizontal and fixed and moment of inertia about it is I. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be.
View SolutionA cord is wound around the circumference of wheel of radius r the axis of the wheel is horizontal and moment of inerita about it is / The weight mg is attached to the end of the cord and falls from rest after falling throgh a distance h the angular velocity of the wheel will be
View SolutionA cord is wound round the circumference of a solid cylinder radius R and mass M. The axis of the cylinder is horizontal. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h.

View Solution

