A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $ω$ is an example of non=inertial frame of reference. The relationship between the force ${\to F}_{r o t}$ experienced by a particle of mass m moving on the rotating disc and the force ${\to F}_{\in}$ experienced by the particle in an inertial frame of reference is
${\to F}_{r o t} = {\to F}_{i n} + 2 m ({\to v}_{r o t} \times \to ω) + m (\to ω \times \to r) \times \to ω$ .
where ${\to v}_{r o t}$ is the velocity of the particle in the rotating frame of reference and $\to r$ is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed $ω$ about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis $(\to ω = ω ˆ k)$ . A small block of mass m is gently placed in the slot at $\to r (R / 2) ˆ i$ at $t = 0$ and is constrained to move only along the slot.

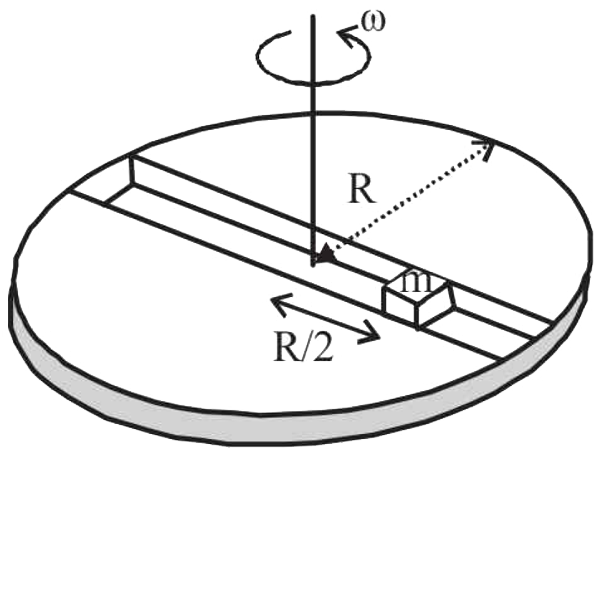
The distance r of the block at time is

$\frac{R}{4} (e^{2 ω t} + e^{- 2 ω t})$

$\frac{R}{4} (e^{ω t} + e^{- ω t})$

$\frac{R}{2} cos 2 ω t$

$\frac{R}{2} cos ω t$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

It is given that X-axis is along the groove and Y-axis is perpendicular to the groove. Z-axis is perpendicular to the plane of the disc.
Above described frame is assumed to be fixed with the axis hence it rotates along with mg the disc. We can understand that in this rotating frame of reference particle is moving along X-axis only. Hence position vector, velocity vector and acceleration vector are directed along the X-axis only.
$\to r = r ˆ i, {\to v}_{r o t} = (d r / d t) ˆ i, \to ω = ω \to k and {\to F}_{r o t} = m (d^{92}) r \frac{)}{{d t}^{2}} ˆ i N_{1}, N_{2}$ and mg shown in figure are real forces which act in inertial frame. Hence we can write the following:
${\to F}_{in} N_{1} ˆ j + (N_{2} - m g) ˆ k ... (i)$
Force acting on the particle with respect to rotating frame of reference is given as follows:
${\to F}_{r o t} = {\to F}_{in} + 2 m ({\to r}_{r o t} \times \to ω) + m (\to ω \times \to r) \times \to ω ... (i i)$
Substituting all values in equation (ii) we get the following:
$m \frac{d^{2} r}{{d t}^{2}} ˆ i [N_{1} ˆ j + (N_{2} - m g) ˆ k] + 2 m (\frac{d r}{d t} ˆ i \times ω ˆ k) + m (ω ˆ k \times r ˆ i) \times ω ˆ k$
$\Rightarrow m \frac{d^{2} r}{{d t}^{2}} ˆ i = m ω^{2} r ˆ i + (N_{1} - 2 m ω \frac{d r}{d t}) ˆ j + (N_{2} - m g) ˆ k$
On comparing the individual components on both the sides of the equation we get
$\frac{d^{2} r}{{d t}^{2}} = ω^{2} r ... (i i i)$
$N_{1} = 2 m ω \frac{d r}{d t} ... (i v)$
$N_{2} = m g ... (v)$
We can see that value ofr given in option (b) satisfies our equation (iv) and also it satisfies the boundary condition of t=0, R/2. Hence option (b) is correct.

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Knowledge Check

A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $ω$ is an example of non=inertial frame of reference. The relationship between the force ${\to F}_{r o t}$ experienced by a particle of mass m moving on the rotating disc and the force ${\to F}_{\in}$ experienced by the particle in an inertial frame of reference is
${\to F}_{r o t} = {\to F}_{i n} + 2 m ({\to v}_{r o t} \times \to ω) + m (\to ω \times \to r) \times \to ω$ .
where ${\to v}_{r o t}$ is the velocity of the particle in the rotating frame of reference and $\to r$ is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed $ω$ about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis $(\to ω = ω ˆ k)$ . A small block of mass m is gently placed in the slot at $\to r (R / 2) ˆ i$ at $t = 0$ and is constrained to move only along the slot.

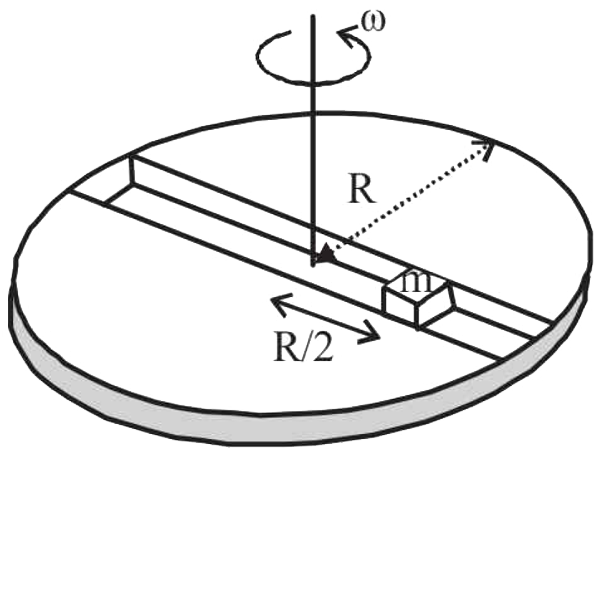
The net reaction of the disc on the block is
A(a) $\frac{1}{2} m ω^{2} R (e^{2 ω t} - e^{- 2 ω t}) ˆ j + m g ˆ k$
B(b) $\frac{1}{2} m ω^{2} R (e^{ω t} - e^{- ω t}) ˆ j + m g ˆ k$
C(c) $- m ω^{2} R cos ω t ˆ j - m g ˆ k$
D(d) $m ω^{2} R sin ω ˆ j - m g ˆ k$
Non-inertial frame of reference have
Azero acceleration.
Bsome acceleration with respect to inertial frame of reference.
Czero velocity.
Dconstant velocity with respect to inertial frame of reference.
An inertial frame of reference is, by definition,
Aa frame moving with uniform velocity w.r.t. earth
Ba frame moving with velocity w.r.t our Sun
Ca frame which is not rotating
Da frame in which Newton's first law of motion is valid.

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )

Home
Ask Doubt
Profile

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Non-inertial frame of reference have

An inertial frame of reference is, by definition,

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )