A disc of mass m and radius r is rotating with angular velocity, on a frictionless horizontal plane about a vertical axis passing through its centre. A ring of same mass and radius is gently placed on it in such a way that centres of both coincide. After some time it is found that both attain a common angular velocity
If we consider disc and ring in a single system then its angular momentum is conserved.
ω=ω03
Loss in K.E. is double to that of final K.E. of the system
Loss in K.E. is 2/3 of initial K.E. of the system.
The correct Answer is:A, B, C, D
To solve the problem, we need to analyze the situation step by step, applying the principles of conservation of angular momentum and kinetic energy.
Step 1: Understand the System
We have a disc of mass m and radius r rotating with an initial angular velocity ω0. A ring of the same mass m and radius r is placed on top of the disc, and they eventually rotate together with a common angular velocity ω.
Step 2: Moment of Inertia Calculation
1. Moment of Inertia of the Disc:
Idisc=12mr2
2. Moment of Inertia of the Ring:
Iring=mr2
3. Total Moment of Inertia of the System (when both are rotating together):
Itotal=Idisc+Iring=12mr2+mr2=32mr2
Step 3: Conservation of Angular Momentum
Since there is no external torque acting on the system, the angular momentum before and after the ring is placed on the disc must be conserved.
1. Initial Angular Momentum:
Linitial=Idisc⋅ω0=(12mr2)⋅ω0
2. Final Angular Momentum (after the ring is placed):
Lfinal=Itotal⋅ω=(32mr2)⋅ω
3. Setting Initial and Final Angular Momentum Equal:
12mr2ω0=32mr2ω
Step 4: Solve for Common Angular Velocity
1. Cancel mr2 from both sides:
12ω0=32ω
2. Rearranging gives:
ω=ω03
Step 5: Calculate Initial and Final Kinetic Energy
1. Initial Kinetic Energy:
Kinitial=12Idiscω20=12(12mr2)ω20=14mr2ω20
2. Final Kinetic Energy:
Kfinal=12Itotalω2=12(32mr2)(ω03)2=12⋅32mr2⋅ω209=112mr2ω20
Step 6: Calculate Loss in Kinetic Energy
1. Loss in Kinetic Energy:
ΔK=Kinitial−Kfinal=14mr2ω20−112mr2ω20
2. Finding a common denominator (12):
ΔK=(312−112)mr2ω20=212mr2ω20=16mr2ω20
Conclusion
The loss in kinetic energy is 16mr2ω20.
We have a disc of mass m and radius r rotating with an initial angular velocity ω0. A ring of the same mass m and radius r is placed on top of the disc, and they eventually rotate together with a common angular velocity ω.
1. Moment of Inertia of the Disc:
Idisc=12mr2
Iring=mr2
Itotal=Idisc+Iring=12mr2+mr2=32mr2
Since there is no external torque acting on the system, the angular momentum before and after the ring is placed on the disc must be conserved.
Linitial=Idisc⋅ω0=(12mr2)⋅ω0
Lfinal=Itotal⋅ω=(32mr2)⋅ω
12mr2ω0=32mr2ω
1. Cancel mr2 from both sides:
12ω0=32ω
ω=ω03
1. Initial Kinetic Energy:
Kinitial=12Idiscω20=12(12mr2)ω20=14mr2ω20
Kfinal=12Itotalω2=12(32mr2)(ω03)2=12⋅32mr2⋅ω209=112mr2ω20
1. Loss in Kinetic Energy:
ΔK=Kinitial−Kfinal=14mr2ω20−112mr2ω20
ΔK=(312−112)mr2ω20=212mr2ω20=16mr2ω20
The loss in kinetic energy is 16mr2ω20.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
Explore 10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
Explore 3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
Explore 48 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View Solution
Knowledge Check
A horizontal disc rotates freely about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is now gently placed on the disc. After some time, the two rotate with a common angular velocity, then
Asome friction exists between the disc and the ringBthe angular momentum of the 'disc plus ring' is conservedCthe final common angular velocity is (23)rd of the initial angular velocity of the discD(23)rd of the initial kinetic energy changes to heatA horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
Ano friction exists between te disc and the ringBthe angular momentum of the system is conservedCthe final common angular velocity is 12ωDall of the aboveA horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -
 A√32ωRBωR2CωRDωR√2
A√32ωRBωR2CωRDωR√2
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
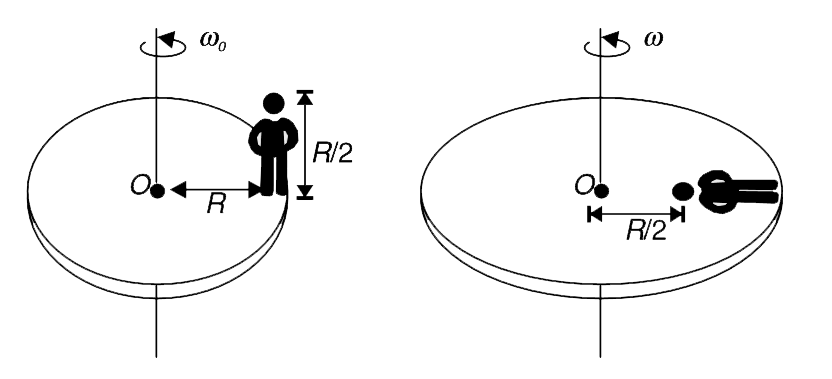
View SolutionA disc of mass M and radius R is rotating with angular velocity ω0 about a vertical axis passing through its centre (O). A man of mass M2 and height R2 is standing on the periphery. The man gradually lies down on the disc such that his head is at a distance R2 from the centre and his feet touching the edge of the disc. For simplicity assume that the man can be modelled as a thin rod of length R2. Calculate the angular speed (ω) of the platform after the man lies down.
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA uniform disc of radius 'a' and mass 'm' is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle of mass 'm' is then suddenly attached to the rim of the disc and rotates with it. The new angular speed is
View SolutionA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
View Solution

