There are two inclined planes A and B of same dimensions. A is sufficiently rough but B is smooth A round shaped object is released from rest at the top point of inclined plane A and acceleration the object is found to be a, and v1 is the velocity of centre of object when it reaches the bottom. When the same process is repeated with B then corresponding values are found to be $a_{2} and v_{2}$ .

A

$a_{1} > a_{2}$

B

$a_{1} < a_{2}$

C

$v_{1} > v_{2}$

D

$v_{1} < v_{2}$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B, D

To solve the problem, we will analyze the motion of a round-shaped object on two inclined planes, A (rough) and B (smooth). We will determine the relationship between their accelerations and final velocities.
1. Understanding the System:
- We have two inclined planes, A and B, with the same dimensions (height and angle).
- Plane A is rough, allowing the object to roll without slipping, while plane B is smooth, causing the object to slide without rolling.
2. Acceleration on Plane A (Rough):
- For the rough inclined plane A, the object rolls down. The acceleration $a_{1}$ can be calculated using the formula:
$a_{1} = \frac{g sin θ}{1 + \frac{I}{m R^{2}}}$
where $I$ is the moment of inertia of the object, $m$ is its mass, $R$ is its radius, and $g$ is the acceleration due to gravity.
3. Acceleration on Plane B (Smooth):
- For the smooth inclined plane B, the object slides down without rolling. The acceleration $a_{2}$ is given by:
$a_{2} = g sin θ$
4. Comparing Accelerations:
- Since $a_{1}$ includes a term in the denominator that is greater than 1 (due to the moment of inertia), we can conclude:
$a_{1} < a_{2}$
5. Velocity at the Bottom of Plane A:
- The final velocity $v_{1}$ of the object when it reaches the bottom of plane A can be found using energy conservation:
$m g h = \frac{1}{2} m v_{1}^{2} + \frac{1}{2} I ω^{2}$
Since $ω = \frac{v_{1}}{R}$ , we can substitute and rearrange to find $v_{1}$ .
6. Velocity at the Bottom of Plane B:
- For plane B, the final velocity $v_{2}$ is calculated similarly:
$m g h = \frac{1}{2} m v_{2}^{2}$
This simplifies to:
$v_{2} = \sqrt{2 g h}$
7. Comparing Velocities:
- Since part of the potential energy on plane A is converted into rotational kinetic energy, less energy is available for linear motion compared to plane B. Thus:
$v_{1} < v_{2}$
Conclusion:
- We find that:
- $a_{1} < a_{2}$ (the acceleration on the rough plane is less than that on the smooth plane).
- $v_{1} < v_{2}$ (the final velocity on the rough plane is less than that on the smooth plane).
Final Answers:
- $a_{1} < a_{2}$
- $v_{1} < v_{2}$

Updated on:18/9/2024

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
A $m^{0}$
B $m$
C $m^{2}$
D $m^{- 1}$
A solid cylinder rolls down from an inclined plane of height h. What is the velocity of the cylinder when it reaches at the bottom of the plane ?
A $\sqrt{\frac{2 g h}{3}}$
B $\sqrt{2 g h}$
C $\sqrt{\frac{4 g h}{3}}$
D $\sqrt{\frac{3 g h}{2}}$
A rolling body is released from rest on sufficient rough long inclined plane of inclination $θ$ . Consider four points A, B, C and D on the sphere. After one revolution.

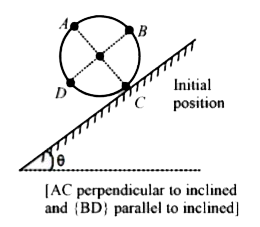AAcceleration of point C is zero.
BAcceleration of point B is along line BD.
CAcceleration of point A is along line AC.
DAcceleration of point C is along line CA.

MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )

Home
Ask Doubt
Profile