Question

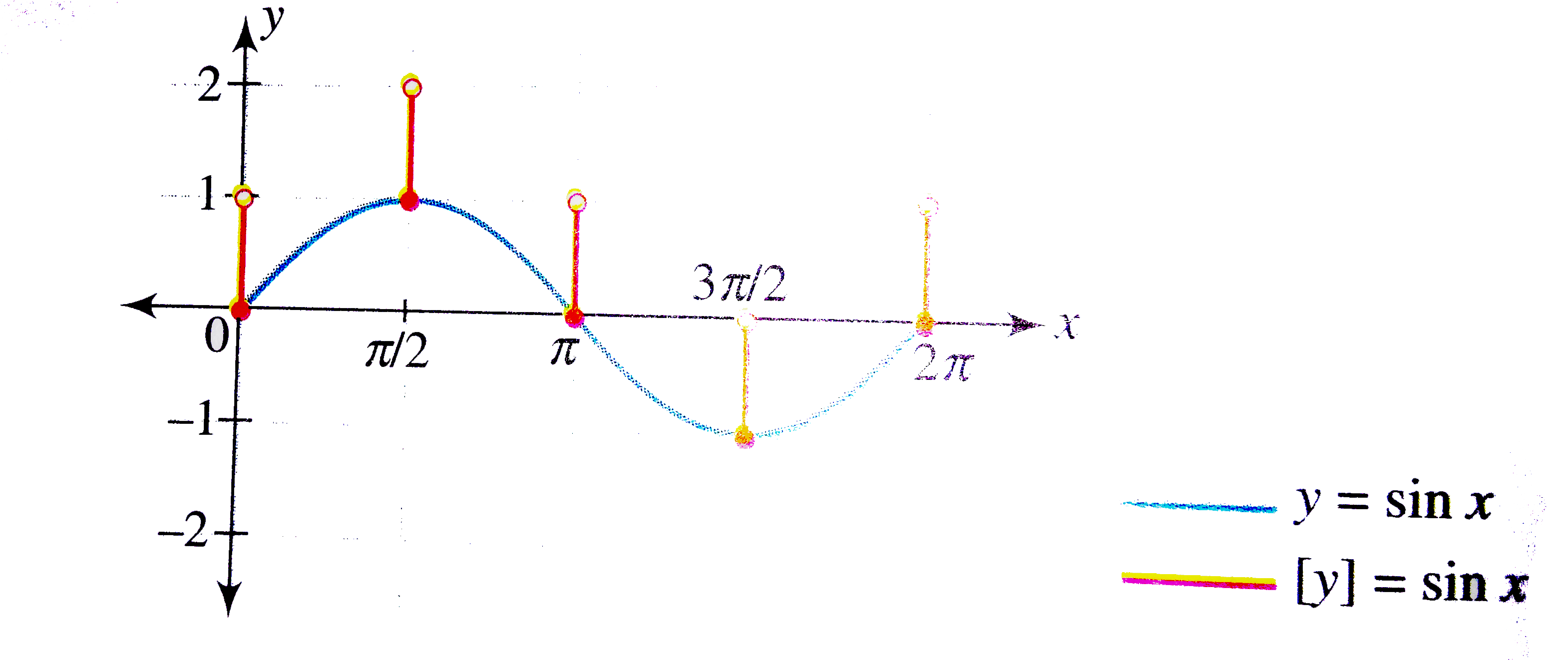
Draw the graph of $\left[y\right]=\sin x,x\in [0,2\pi ]$ where $[\cdot ]$ denotes the greatest integer function

Explanation

We have [y] = sin x
This is satisfied by intergral values of sin x only. So
sin x = -1, 0, 1
When `sin x = -1, x = (4n - 1)(pi)/(2), n in Z`
And `[y] = -1 therefore - 1 le y lt 0`
When `sin x = 1, x (4n + 1)(pi)/(2), n in Z`
And `[y] = 1 therefore 1 le y lt 2`
When `sin x = 0, x = npi, n in Z`
And `[y] = 0 therefore 0 le y lt 1`
Hence the graph of the function is as shown in the following figure.

Drawing the graph of `g(x) = f(x) sin x`
We have `g(x) = f(x) sin x`.
Since `-1 le sin x le 1`, we have `-f(x) le f(x) sin x le f(x)`.
Thus the graph of `g(x) = f(x)` sin x lies between th graphs of `y = f(x)` and y = -f(x). So the draw the graph of y = g(x), we first draw the graph of y = f(x) and y = -f(x) and plot the points of the graph for quadrant angles, i.e. `x = ... -pi, -pi//2, 0, pi//2, pi, 3pi//2, 2pi...`
`g(pi//2) = f(pi//2) " sin " (pi//2) = f(pi//2),` thus the point `(pi//2, f(pi//2))` lies on the graph of y = f(x)
`g(3pi//2) = f(3pi//2) " sin " (3pi//2) = -f(3pi//2),` thus the point `(3pi//2, - f(3pi//2))` lies on the graph of y = -f(x).
Similarly, for `x = 5pi//2, 9pi//2, ...` points of y = g(x) lie on the graph of y = f(x), and for `x = 3pi//2, 7pi//2, ...` points of y = g(x) lie on the graph of y = -f(x).