Question

Draw the graph of $y=\left[\sin x\right],x\in [0,2\pi ],$ where $[\cdot ]$ represents the greatest integer function.

Explanation

We have `y = f(x) = [sin x], x in [0, 2pi]`
Let the first draw the graph of `y = sin x, x in [0, 2pi]`.

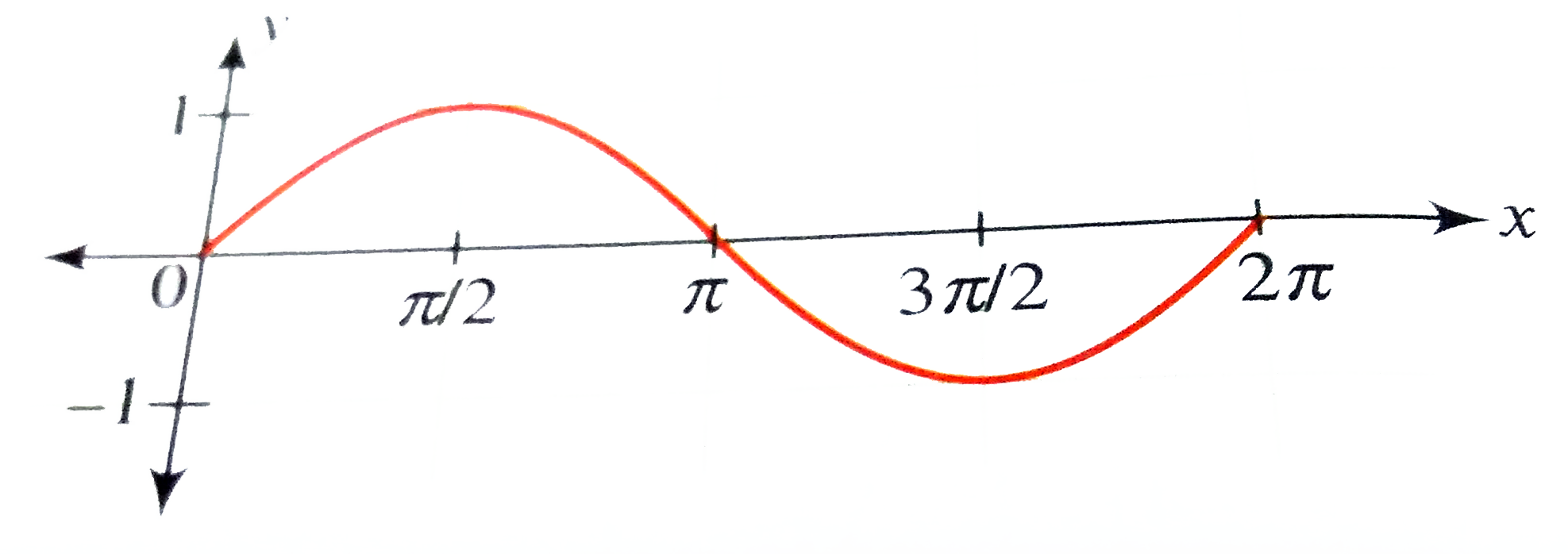
Let the first consider the intergrel values of sin x and hence [sin x].
`f(0) = [sin 0] = 0`
`f(pi//2) = [sin (pi//2)] = 1`
`f(x) = [sin pi] = 0`
`f(3pi//2) = [sin(3pi//2)] = -1`
`f(2pi) = [sin(2pi)] = 0`

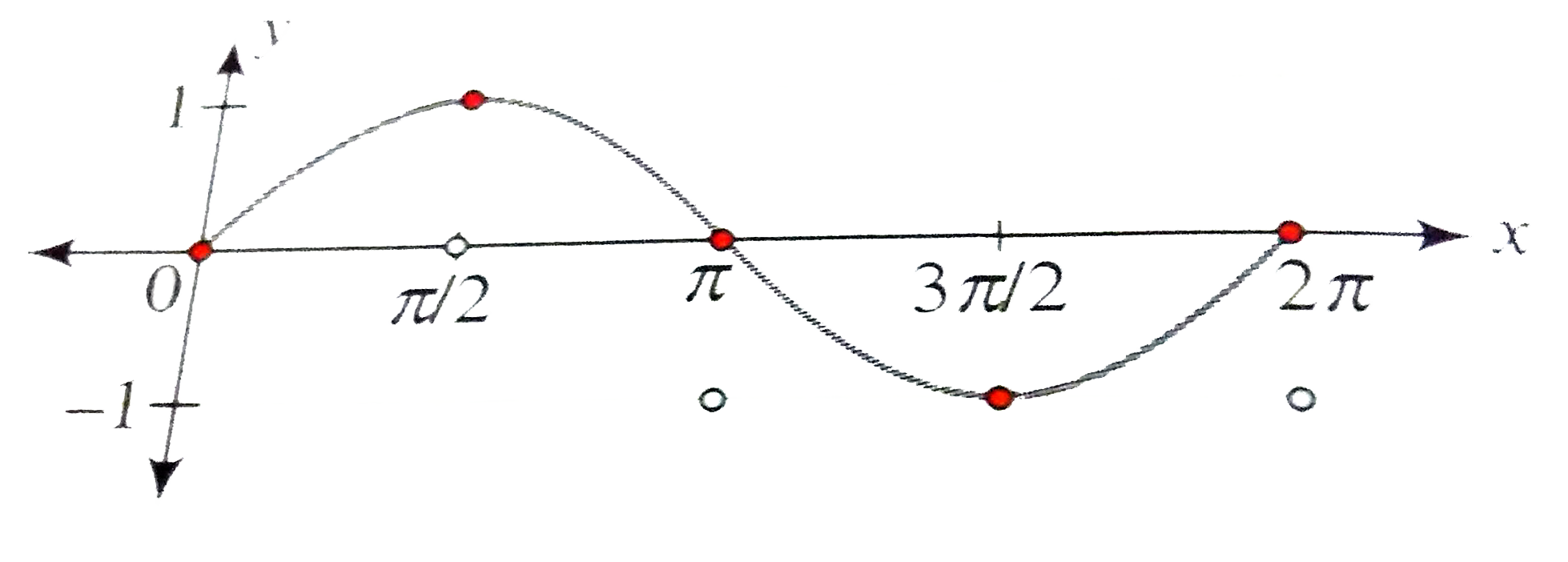
Now let us consider the values of y = sin x in quadrants.
In `1^(st)` quadrant `(0 lt x lt pi//2), 0 lt sin x lt 1`
`therefore ` [sin x] = 0
In `2^(nd)` quadrant `(pi//2 lt x lt pi), 0 lt sin x lt 1`
`therefore ` [sin x ] = 0
In `3^(rd)` quadrant `(pi lt x lt 3pi//2), - 1 lt sin x lt 0`
`therefore ` [sin x] = -1
In `4^(th)` quadrant `(3pi//2 lt x lt 2pi) - 1 lt sin x lt 0`
`therefore` [sin x] = -1
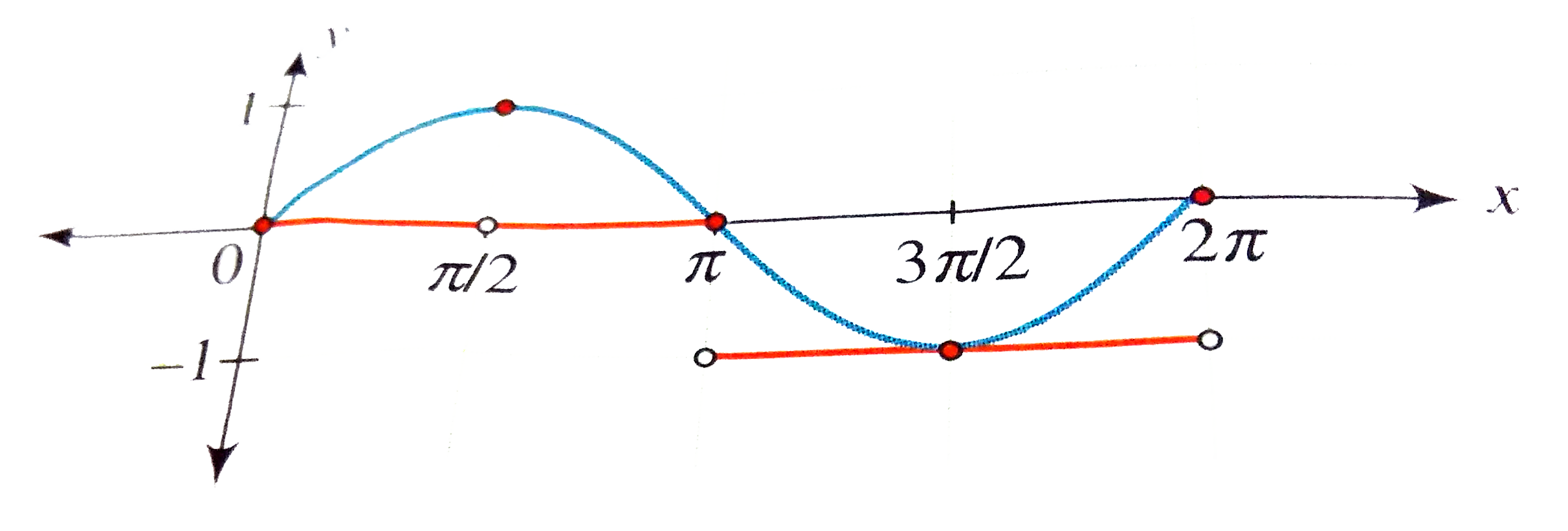
Thus, the graph of `f(x) = [sin x]` is shown in the following figure.