Doubtnut Promotions Sticky

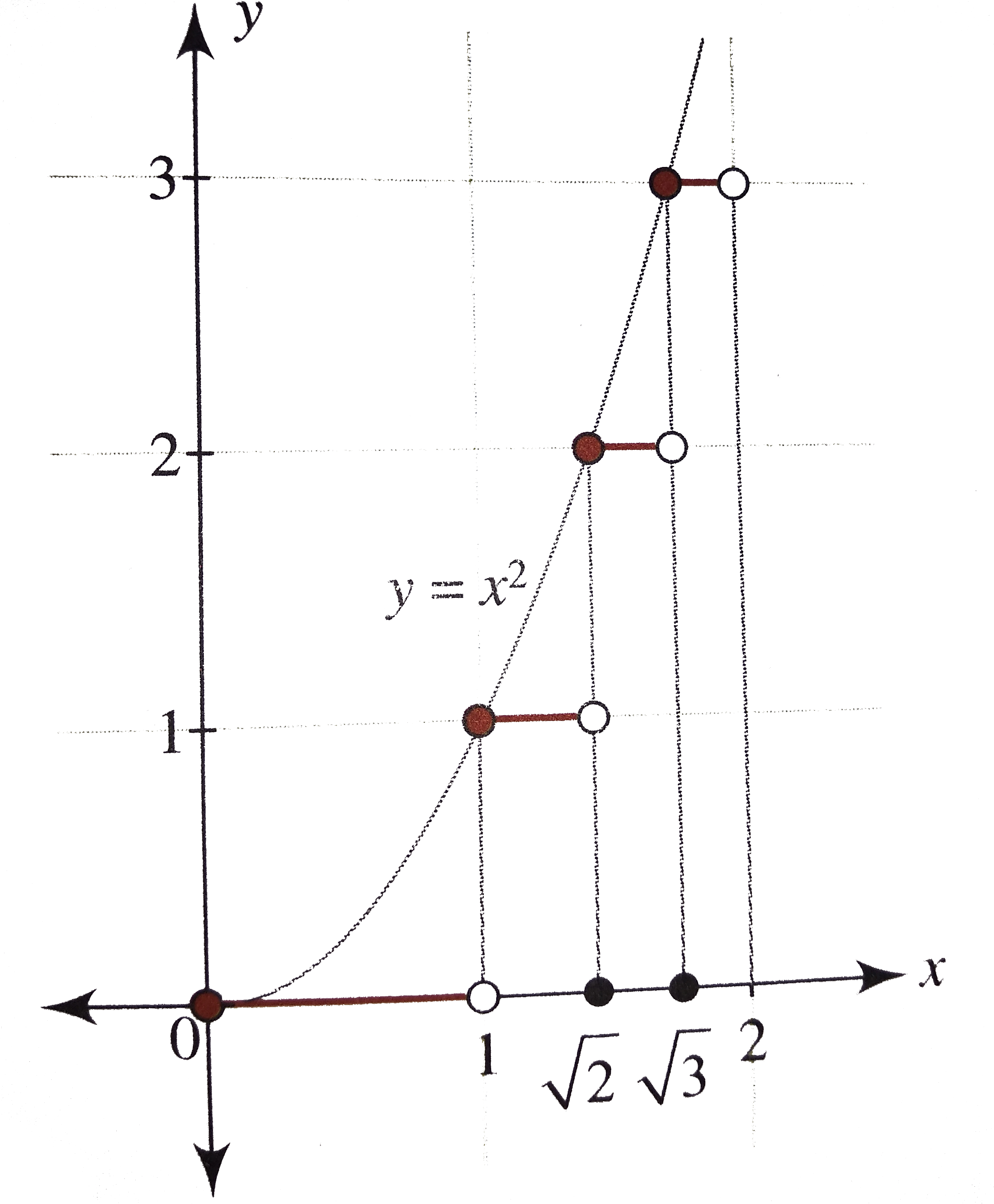
Draw the graph of f(x)=[x2],x∈[0,2), where [⋅] denotes the greatest integer function.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

f(x)=[x2],x∈[0,2)
y=x2 is a monotonically increasing function in x∈[0,2).
So f(x)=[x2] will be discontinuous when x2 is an integer.
For x∈[0,2),x2∈[0,4)
So [x2] is discontinuous when x2=1,2,3orx=1,√2,√3.
f(x)=[x2]=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0,x∈[0,1)orx2∈[0,1)1,x∈[1,√2)orx2∈[1,2)2,x∈[√2,√3)orx2∈[2,3)3,x∈[√3,2)orx2∈[3,4)
The graph of the function is as shown in the following figure.
ocr_image

|
Updated on:21/07/2023
Class 12MATHSFUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let f(x) =[x]2+[x+1]−3, where [.] denotes the greatest integer function. Then

    Af(x)≠0 for all real values of x
    Bf(x) = 0 for only two real value of x
    Cf(x) = 0 for infinite values of x.
    Df(x) = 0 for no real value of x
  • Question 2 - Select One

    The function f(x)=[x2]+[−x]2, where [.] denotes the greatest integer function, is

    Acontinuous and derivable at x=2
    Bneither continuous nor derivable at x=2
    Ccontinuous but not dervable at x=2
    Dnone of these
  • Question 3 - Select One

    If f(x)=[x]|x|,x≠0, where [.] denotes the greatest integer function, then f'(1) is

    A−1
    B1
    Cnon-existent
    Dnone of these