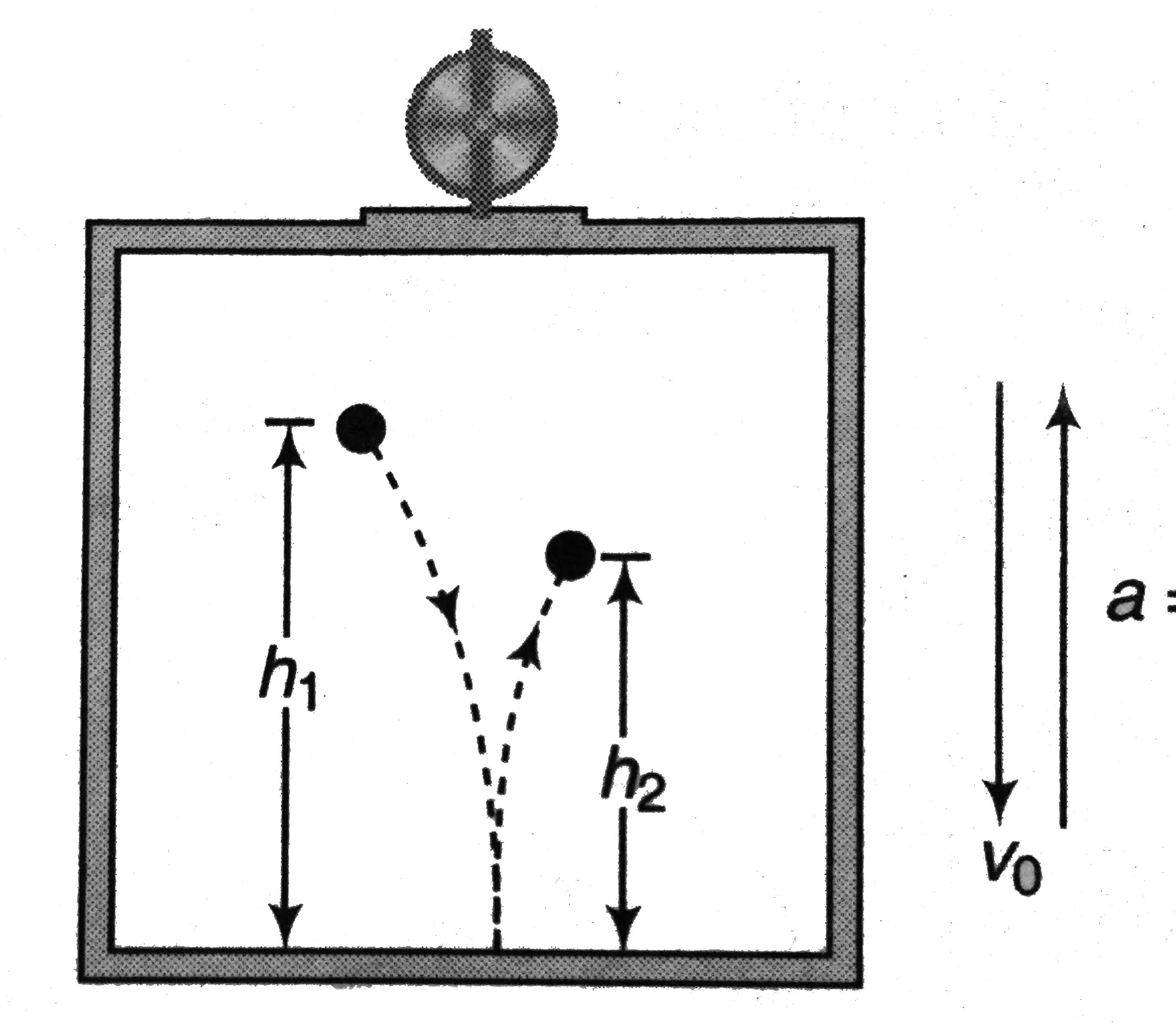
A ball is released from rest relative to the elevator at a distance h1 above the floor. The speed of the elevator at the time of ball release is v0. Determine the bounce height h2 relative to elevator of the ball (a) if v0 is constant and (b) if an upward elevator accleration a=g4 begins at the instant the ball is released. The coefficient of restitution for the impact is e.
The correct Answer is:A, B
(a) ur=0, ar=g
∴vr=√2gh1
After collision relative velocity
vr'=e√2gh1
and relative retardation is still g (downwards).
Hence,
h2=(vr')22g=e2h1
(b) ur=0, ar=g+g4=5g4
∴ Just before collsion vr=√2(5g4)h1
Just after collision vr'=evr.
Relative retardation is still 5g4.
Hence, h2=(vr')22(5g4)=e2h1
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Comprehension Based Questions
Explore 3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
Similar Questions
A ball of mass m is released from rest relative to elevator at a height h, above the floor of the elevator. After making collision with the floor of the elevator it rebounces to height h2. The coefficient of restitution for Collision is e. For this situation, mark the correct statement(s).

View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
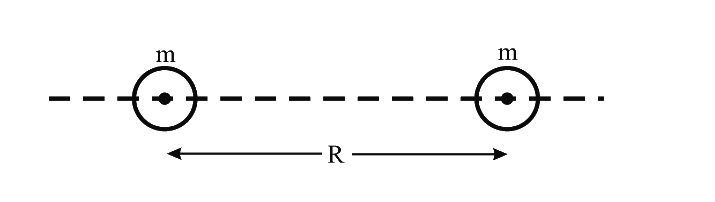
View SolutionTwo balls of radius r each are placed at a distance R and released . The speed of each ball when they collide
View SolutionA stone is released from an elevator going up with an acceleration of g2. What is the acceleration of the stone just after release ?
View SolutionA ball is released from a height and it reaches the ground in 3 s. If g=9.8m s−2, find the value of the height from which the ball was released.
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View Solution

