A system of binary stars of mass $m_{A}$ and $m_{B}$ are moving in circular orbits of radii $r_{A}$ and $r_{B}$ respectively. If $T_{A}$ and $T_{B}$ are at the time periods of masses $m_{A}$ and $m_{B}$ respectively then

A

$\frac{T_{A}}{T_{B}} = {(\frac{r_{A}}{r_{B}})}^{3 / 2}$

B

$T_{A} > T_{B} (if r_{A} > r_{B})$

C

$T_{A} > T_{B} (if m_{A} > m_{B})$

D

$T_{A} = T_{B}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$\frac{G m_{A} m_{B}}{{(r_{A} + r_{B})}_{A}^{2}} = \frac{m_{A} r_{A} 4 π^{2}}{T_{A}^{2}} = \frac{m_{B} r_{B} 4 π^{2}}{T_{B}^{2}}$
$\Rightarrow m_{A} r_{A} = m_{B} r_{B}$
$∴ T_{A} = T_{B}$

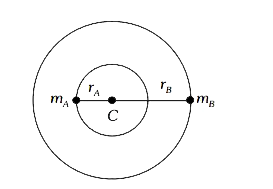
Aliter : The gravitational force of attraction between the stars will provide the necessary centripetal force. In this case angular velocity of both stars is the same. Hence $T_{A} = T_{B}$ .

Updated on:21/07/2023

|

Class 11 PHYSICS GRAVITATION

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile