Two stars of mass are in circular orbits around their centre of mass The star of mass has an orbit of radius the star of mass has an orbit of radius (assume that their centre of mass is not acceleration and distance between starts is fixed)
(a) Show that the ratio of orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is
(b) Explain why the two stars have the same orbital period and show that the period
.
The correct Answer is:
.
Step by step video, text & image solution for Two stars of mass M_(1) & M_(2) are in circular orbits around their centre of mass The star of mass M_(1) has an orbit of radius R_(1) the star of mass M_(2) has an orbit of radius R_(2) (assume that their centre of mass is not acceleration and distance between starts is fixed) (a) Show that the ratio of orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is R_(1)//R_(2) = M_(2)//M_(1) (b) Explain why the two stars have the same orbital period and show that the period T=2pi((R_(1)+R_(2))^(3//2))/(sqrt(G(M_(1)+M_(2)))) . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The two stars in a certain binary star system move in circular orbits The first star α moves in an orbit of radius 1.00×109km The other star β moves in an orbit of radius 5.00×108km What is the ratio of masses of star β to the star α ? .
View SolutionA satellite of mass Ms is revolving around the earth (Mass M) in a orbit of radius R. Find its angular momentum.
View Solution
Knowledge Check
Two stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
A2π√r32G(m1+m2)B2π√r3(m1+m2)2Gm1m2C2π√2r3G(m1+m2)D2π√r3G(m1+m2)The binding of a satellite of mass m in a orbit of radius r is
AmgR2rBmgR22rC−mgR3rD−mgR32rIn a double star system one of mass m1 and another of mass m2 with a separation d rotate about their common centre of mass. Then rate of sweeps of area of star of mass m1 to star of mass m2 about their common centre of mass is
Am1m2Bm2m1Cm21m22Dm22m21
A solid spher of mass m1 density ρ1 radius R1 and a solid cone of mass m2 density ρ2. Radius R2, are arranged as shown in the figure. The centre of mass is located at
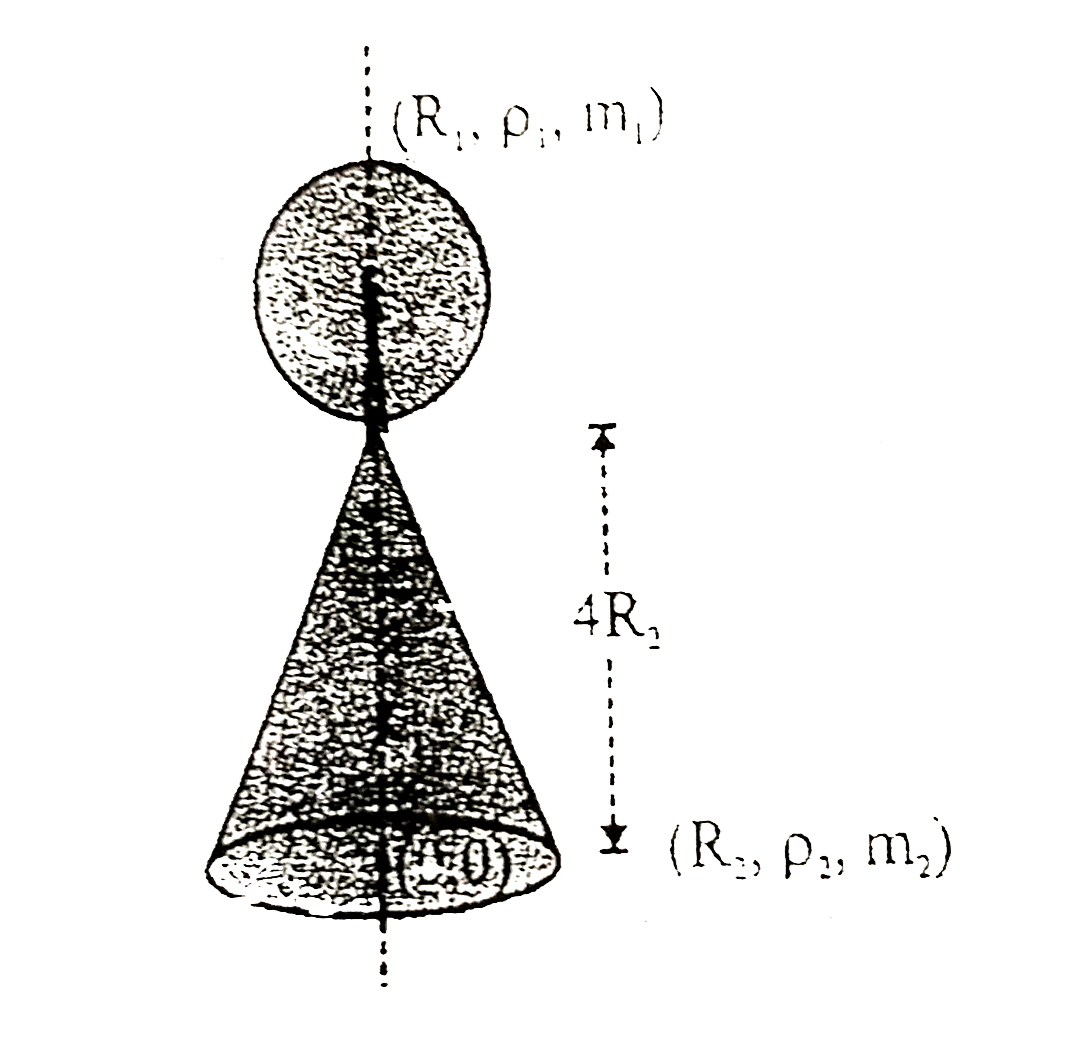
View SolutionEnergy required to move a body of mass m from an orbit of radius 2R to 3R is
View SolutionIn order to shift a body of mass m from a circular orbit of radius 3R to a higher orbit of radius 5R around the earth, the work done is
View SolutionA satellite of mass M revolving in a circular orbit of radius rs around the earth of mass M has a total energy E. then, its angular momentum will be
View SolutionTwo stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The period of revolution is :
View Solution
