The two stars in a certain binary star system move in circular orbits The first star α moves in an orbit of radius 1.00×109km The other star β moves in an orbit of radius 5.00×108km What is the ratio of masses of star β to the star α ? .
The correct Answer is:2
To find the ratio of the masses of star beta to star alpha in a binary star system, we can use the concept of the center of mass. The two stars revolve around their common center of mass, and the distances from the center of mass are inversely proportional to their masses.
1. Identify the Radii of Orbits:
- The radius of the orbit of star alpha, rα=1.00×109km
- The radius of the orbit of star beta, rβ=5.00×108km
2. Use the Center of Mass Concept:
- For two objects in a binary system, the relationship between their masses and their distances from the center of mass is given by:
mα⋅rα=mβ⋅rβ
3. Rearrange the Equation:
- We want to find the ratio of the masses mβmα:
mβmα=rαrβ
4. Substitute the Values:
- Plug in the values of rα and rβ:
mβmα=1.00×109km5.00×108km
5. Calculate the Ratio:
- Simplifying the ratio:
mβmα=1.000.50=2
6. Final Result:
- The ratio of the masses of star beta to star alpha is:
mβmα=2
Summary:
The ratio of the masses of star beta to star alpha is 2.
---
- The radius of the orbit of star alpha, rα=1.00×109km
- The radius of the orbit of star beta, rβ=5.00×108km
- For two objects in a binary system, the relationship between their masses and their distances from the center of mass is given by:
mα⋅rα=mβ⋅rβ
- We want to find the ratio of the masses mβmα:
mβmα=rαrβ
- Plug in the values of rα and rβ:
mβmα=1.00×109km5.00×108km
- Simplifying the ratio:
mβmα=1.000.50=2
- The ratio of the masses of star beta to star alpha is:
mβmα=2
The ratio of the masses of star beta to star alpha is 2.
Topper's Solved these Questions
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:EXERCISE-2 PART-3
Explore 12 Videos
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:EXERCISE-2 PART-4
Explore 9 Videos
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:EXERCISE-2 PART-1
Explore 16 Videos
- GEOMATRICAL OPTICS Book:RESONANCEChapter:GEOMATRICAL OPTICS Exercise:Advance level Problems
Explore 35 Videos
- NUCLEAR PHYSICSBook:RESONANCEChapter:NUCLEAR PHYSICSExercise:Advanced level solutions
Explore 16 Videos
Similar Questions
Two stars of mass M1&M2 are in circular orbits around their centre of mass The star of mass M1 has an orbit of radius R1 the star of mass M2 has an orbit of radius R2 (assume that their centre of mass is not acceleration and distance between starts is fixed)
(a) Show that the ratio of orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is R1/R2=M2/M1
(b) Explain why the two stars have the same orbital period and show that the period
T=2π(R1+R2)3/2√G(M1+M2) .
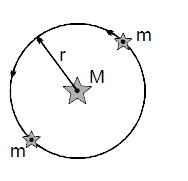
View SolutionA certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
View Solution
Knowledge Check
_S01_034_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The orbital velocity of each star isA54√10×10/sB54√10×105m/sC54√10×102m/sD54√10×104m/s_S01_033_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The mass m of the outer stars is:A1615×1030kgB118×1033kgC1516×1030kgD811×1030kg_S01_035_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The total machanical energy of the system isA−137564×1035JB−137564×1038JC−137564×1034JD−137564×1037J
The mean orbital radius of the Earth around the Sun is 1.5×108km. Estimate the mass of the Sun.
View SolutionTwo planets of equal mass orbit a much massive star (figure). Planet m1 moves in circular orbit of radius 1×108km with period 2yr. Planet m2 moves in an elliptical orbit with closed distance r1=1×108km and farthest distance r2=1.8×108km, as shows.
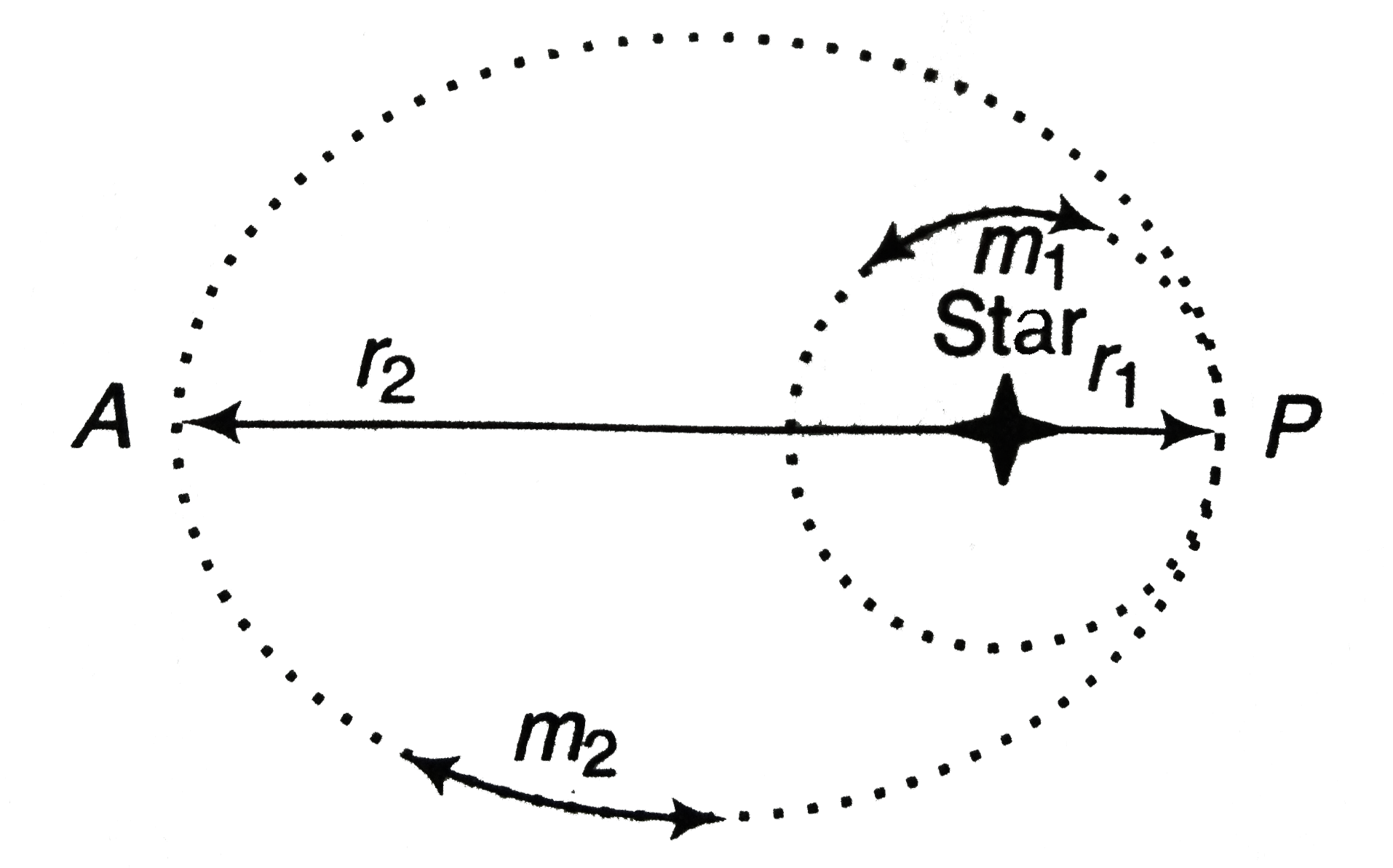
(a) Using the fact that the mean radius of an elliptical orbit is the length of the semi-major axis, find the period of m2's orbit.
(b) Which planet has the greater speed at point P? Which has the greater total energy?
(c ) Compare the speed of planet m2 at P with that at A.
View SolutionA binary star system consists of two stars of masses M1 and M2 revolving in circular orbits of radii R1 and R2 respectively. If their respective time periods are T1 and T2, then
View SolutionThe period of revolution of a planet around the sun in a circular orbit is same as that of period of similar planet revolving around a star of twice the raduis of first orbit and if M is the mass of the sun then the mass of star is
View SolutionA binary star system consists of two stars A and B which have time period TAandTB,radiusRBa and mass MaandMB. Then
View Solution